声明
本篇文章内容均来自于左程云在b站的最新免费算法课。
在学习过程中发现,老师的PPT比较简洁,一些讲出来的技巧与细节并没有写出来。
所以决定做个笔记,记录一些解题思路与技巧,中途可能会写一些自己的理解。
本篇内容为图的建立
内容来自左老师最新算法课程的第59节建图、链式前向星、拓扑排序,链接见下。
https://www.bilibili.com/video/BV1rj411k7tS/?spm_id_from=333.999.0.0&vd_source=e7336779d112d0aaf8054a1f32f59867
内容主要讲我对链式前向星的理解。
代码摘自左神的代码库。
对代码和算法还是不理解,可以看左神的视频,讲的很详细,我不过是表达一下我都这个方法的理解。
建图
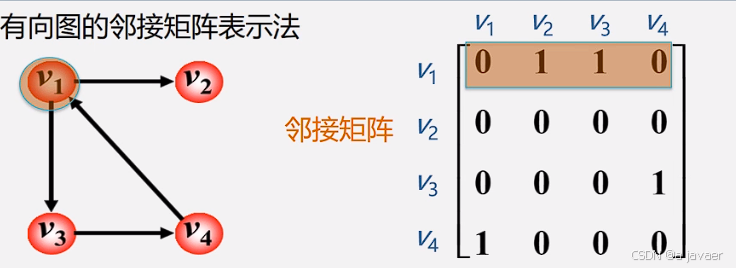
邻接矩阵法
表示方法(图片来自王卓老师的数据结构与算法课)
无向图:
有向无权图:
有向有权图:
当然对于题目来说,给出的输入一般都是[1,2],表示结点1和结点2之间有一条边,若是有权值的图则是[1,2,8],第三位代表边的权值。
缺点:
比如我有一个有n = 10^5个结点的图
我们建图就要一个10^5 * 10^5=10^10大小的图,这超过了一般题目的允许计算量
TIPS:
这里提到题目允许的计算量,一般算机一秒能运行5 x 10^8
如果题目限制1秒,那么算法执行计算次数的数量级应该就在10^8 。
所以邻接矩阵只适用于n不大时,老师说一般1000-2000以内可以接受。
(算法题中不同复杂度算法能处理的数据范围见附录)
邻接表法(最常用)
对每个点拉一个数组,存放与他相邻的结点。
有向无权图:
给出1,2,3,4四个点,
边[1,3] , [4,3],[2,4],[1,2]
所以
结点1的邻接表为{2,3}
结点2的邻接表为{2,4}
把这些数组都放到一个数组中,这样表示一张无权图
即ArrayList<ArrayList<>>
但是有权值的呢?
每个节点的邻接表内部的结点是一个长度2的数组,记录本节点指向哪个节点,权值为多少
ArrayList<ArrayList<int []>>
比如之前的例子,现在有[1,3,6],[1,2,9]这两条表,节点1的邻接表:
{[3,6],[2,9]},第一位代表相连指向节点,第二位表示权值。
链式前向星
前面两种建表其实课上学过,这个我确实没学过。确实很巧妙,但是笔试应该不常用,主要是竞赛吧。我觉得可以作为兴趣了解。
head数组下标代表结点号,head[i]表示点i为起点的 最新加入的一条边的边号。
next数组,下标代表边号,next[i]表示与边i起点相同的上一条加入的边。
to数组, 下标代表边号,to[i]表示边i的终点。
看概念很难理解,来看个例子。
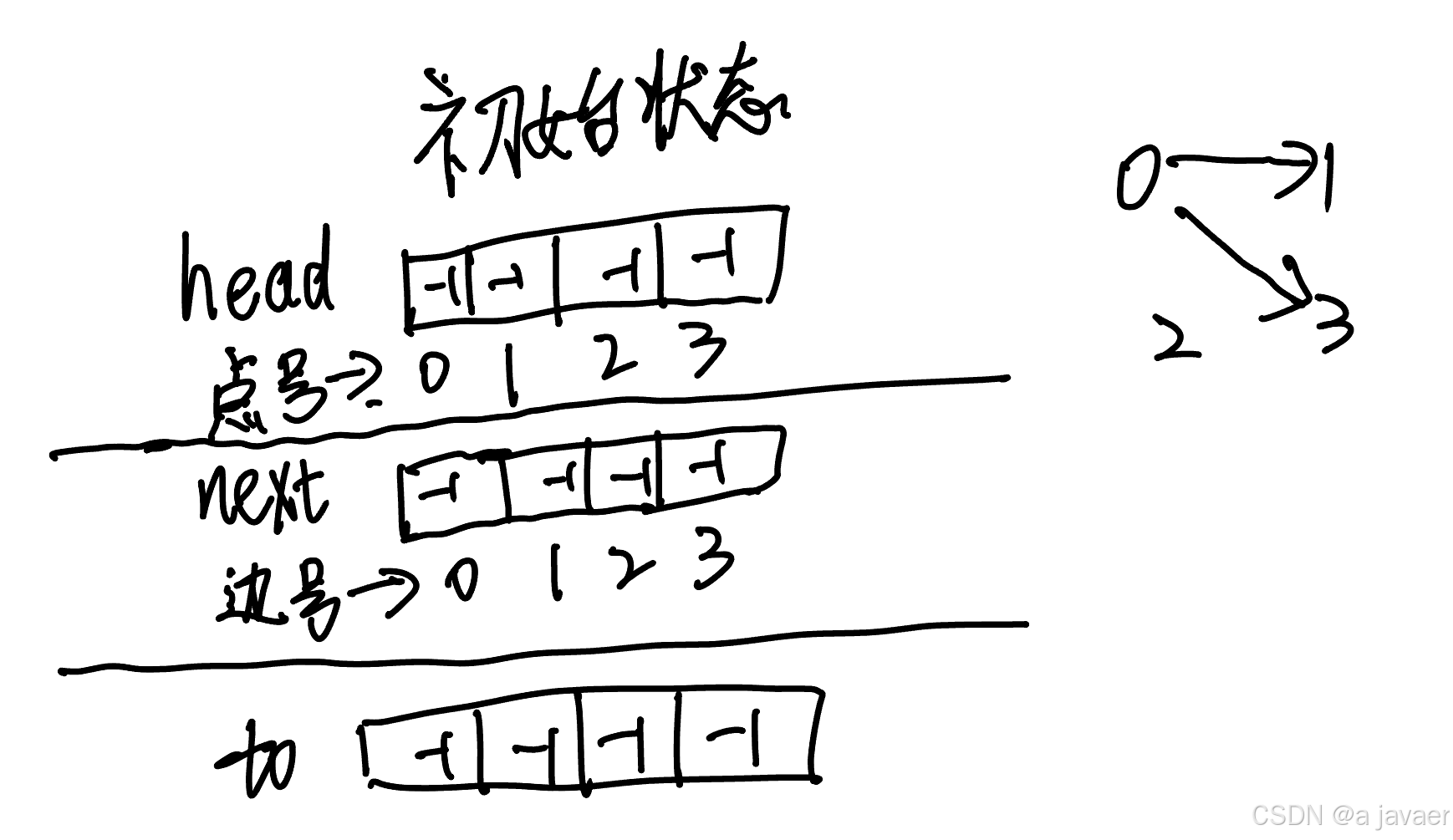
例子:
有结点0,1,2,3
两条边 边0[0,1] 边1[0,3]。
-1为初始值。
注意,在开始时,我们整个数组代表没有边,只有孤立的点,依次加边,三个数组就可以表示一个给出的图。
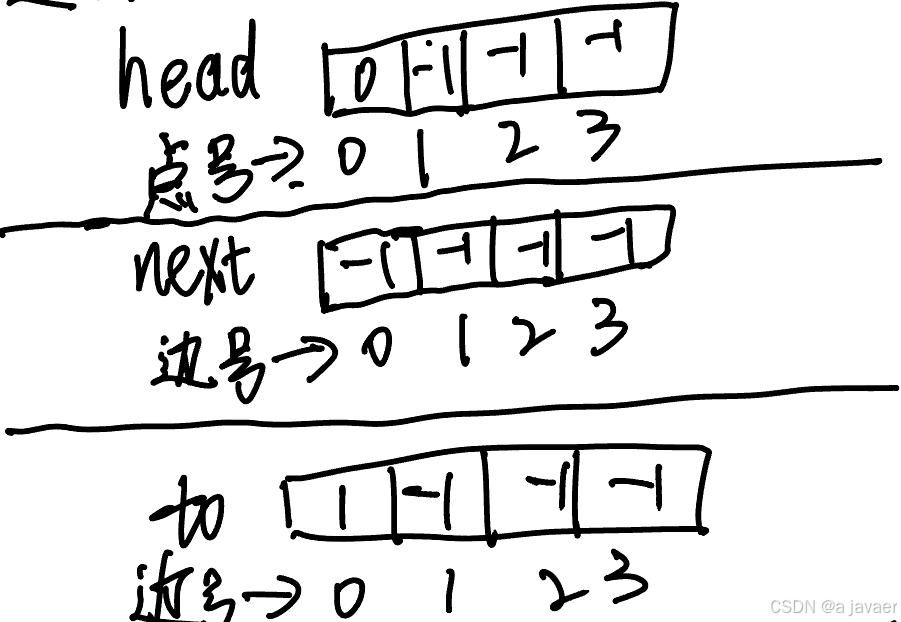
第一次加边
边0[0,1]。
先修改next,next[i]表示与边i起点相同的,上一个加入的边的边号,换一种说法为除本次新加的边外,与新加边起点相同的最新加入的边。
这里next[0],就是除本次加边外 起点为0新加入的边,而head[i]正好表示的是对应结点i为起点最新加入的一条边。head[0]就是0为起点最新加入的边,显然我们除了本次加边,我们还没修改过数组,所以没有最新边,则next[0]为-1。
to[i]表示边i的终点,边0终点为1,则to[0]=1。
最后更新这个head[],本次更新边的起点为0,边号为0,所以head[0]=0。表示起点为0的最新边为边0。
这里完成了一个加边。那么我们现在可以遍历新加的一条边
head[0]=0,点0的最新边为0。表示边0起点为0
to[0]=1,边0终点为1。
next[0]=-1,表示点0为起点的边没有了。
那么第二次加边。
先更新next,边1,next[1]。除本次加边外,与边1同起点的最新边,即当前图中点0为起点的最新边,是刚才加入的边0(起点为0,终点为1)。那么这是我们脑推,从代码看就是head[0]的值,即当前图中最新加入的结点0为起点的边的边号。head[0]=0。使用next[1]=0。
我们发现这样就可以通过next向前遍历同起点的边。因为next中对同起点的边的上一条边做了记录。
下面更新to[1],边1终点3,to[1]=3。
最后更新head,本次加边1,起点为0,则更新head[0]。最新边号为本次加入边,为边1。head[0]=1。
这样第二条边加完了。
我们来看看是否能遍历完一个节点为起点的所有边。
我们遍历0结点为起点的所有边,先看head[0],0结点为起点的最新边为边1,那么再看to[1],可以得知,边1的起点为0,终点为3,[0,3]。
则边1遍历完成,然后遍历下一条边,next[1]表示0结点为起点的上一条边,next[1]=0,同样起点为0的上一条边为边0,终点to[0]=1,边0,[0,1]。
边0遍历完成,再去next[0]看0结点为起点的上一条边,发现next[0]为-1,表示没边了。
则起点为0的两条边都遍历到了。
就是通过next数组记录的遍历顺序,相当于对相同起点的边我们通过next数组可以逐步的根据加入顺序从后向前遍历。
这里的例子加上其他节点的边也是一样成立。
代码
来自老师的课程开放代码
可以直接运行
package class059;
import java.util.ArrayList;
import java.util.Arrays;
public class Code01_CreateGraph {
// 点的最大数量
public static int MAXN = 11;
// 边的最大数量
// 只有链式前向星方式建图需要这个数量
// 注意如果无向图的最大数量是m条边,数量要准备m*2
// 因为一条无向边要加两条有向边
public static int MAXM = 21;
// 邻接矩阵方式建图
public static int[][] graph1 = new int[MAXN][MAXN];
// 邻接表方式建图
// public static ArrayList<ArrayList<Integer>> graph2 = new ArrayList<>();
public static ArrayList<ArrayList<int[]>> graph2 = new ArrayList<>();
// 链式前向星方式建图
public static int[] head = new int[MAXN];
public static int[] next = new int[MAXM];
public static int[] to = new int[MAXM];
// 如果边有权重,那么需要这个数组
public static int[] weight = new int[MAXM];
public static int cnt;
public static void build(int n) {
// 邻接矩阵清空
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
graph1[i][j] = 0;
}
}
// 邻接表清空和准备
graph2.clear();
// 下标需要支持1~n,所以加入n+1个列表,0下标准备但不用
for (int i = 0; i <= n; i++) {
graph2.add(new ArrayList<>());
}
// 链式前向星清空
cnt = 1;
Arrays.fill(head, 1, n + 1, 0);
}
// 链式前向星加边
public static void addEdge(int u, int v, int w) {
// u -> v , 边权重是w
next[cnt] = head[u];
to[cnt] = v;
weight[cnt] = w;
head[u] = cnt++;
}
// 三种方式建立有向图带权图
public static void directGraph(int[][] edges) {
// 邻接矩阵建图
for (int[] edge : edges) {
graph1[edge[0]][edge[1]] = edge[2];
}
// 邻接表建图
for (int[] edge : edges) {
// graph2.get(edge[0]).add(edge[1]);
graph2.get(edge[0]).add(new int[] { edge[1], edge[2] });
}
// 链式前向星建图
for (int[] edge : edges) {
addEdge(edge[0], edge[1], edge[2]);
}
}
// 三种方式建立无向图带权图
public static void undirectGraph(int[][] edges) {
// 邻接矩阵建图
for (int[] edge : edges) {
graph1[edge[0]][edge[1]] = edge[2];
graph1[edge[1]][edge[0]] = edge[2];
}
// 邻接表建图
for (int[] edge : edges) {
// graph2.get(edge[0]).add(edge[1]);
// graph2.get(edge[1]).add(edge[0]);
graph2.get(edge[0]).add(new int[] { edge[1], edge[2] });
graph2.get(edge[1]).add(new int[] { edge[0], edge[2] });
}
// 链式前向星建图
for (int[] edge : edges) {
addEdge(edge[0], edge[1], edge[2]);
addEdge(edge[1], edge[0], edge[2]);
}
}
public static void traversal(int n) {
System.out.println("邻接矩阵遍历 :");
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
System.out.print(graph1[i][j] + " ");
}
System.out.println();
}
System.out.println("邻接表遍历 :");
for (int i = 1; i <= n; i++) {
System.out.print(i + "(邻居、边权) : ");
for (int[] edge : graph2.get(i)) {
System.out.print("(" + edge[0] + "," + edge[1] + ") ");
}
System.out.println();
}
System.out.println("链式前向星 :");
for (int i = 1; i <= n; i++) {
System.out.print(i + "(邻居、边权) : ");
// 注意这个for循环,链式前向星的方式遍历
for (int ei = head[i]; ei > 0; ei = next[ei]) {
System.out.print("(" + to[ei] + "," + weight[ei] + ") ");
}
System.out.println();
}
}
public static void main(String[] args) {
// 理解了带权图的建立过程,也就理解了不带权图
// 点的编号为1...n
// 例子1自己画一下图,有向带权图,然后打印结果
int n1 = 4;
int[][] edges1 = { { 1, 3, 6 }, { 4, 3, 4 }, { 2, 4, 2 }, { 1, 2, 7 }, { 2, 3, 5 }, { 3, 1, 1 } };
build(n1);
directGraph(edges1);
traversal(n1);
System.out.println("==============================");
// 例子2自己画一下图,无向带权图,然后打印结果
int n2 = 5;
int[][] edges2 = { { 3, 5, 4 }, { 4, 1, 1 }, { 3, 4, 2 }, { 5, 2, 4 }, { 2, 3, 7 }, { 1, 5, 5 }, { 4, 2, 6 } };
build(n2);
undirectGraph(edges2);
traversal(n2);
}
}
附录
算法题中不同复杂度算法能处理的数据范围
转自https://blog.csdn.net/qq_40763929/article/details/86726906
在竞赛中,一般算机一秒能运行5 x 10^8次计算,如果题目给出的时间限制1s,那么你选择的算法执行的计算次数最多应该在10^8量级オ有可能解决这个题目。
O(n)的算法能解决的数据范围在n < 10^8。
O(n *logn)的算法能解决的数据范围在n <= 10^6。
O(n*sqrt(n) )的算法能解决的数据范围在n < 10^5。
O(n^2)的算法能解决的数据范围在n<5000。
O(n^3)的算法能解决的数据范围在n <300。
O(2^n)的算法能解决的数据范围在n < 25。
O(n!)的算法能解决的数据范围在n < 11。
以上范围仅供参考,实际中还要考虑每种算法的常数。
结语
我淦,链式前向星我理解用了不长时间。但是写出来想讲明白还是挺难的,要想怎么写能让人明白。也算是费曼学习法了。
本文主要讲图的建立的思想,对于代码没有多涉及。直接搬了左神的代码。
因为代码还挺简单的。
写了2个小时多,真的累。
如果对你有帮助,可以点个赞。
后续不定时更新。