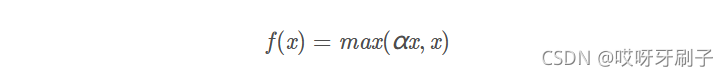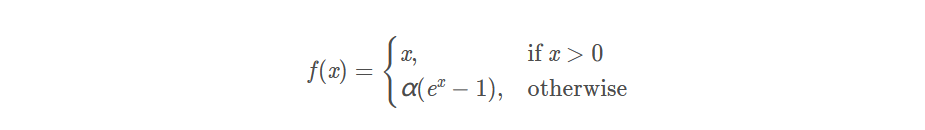- 激活函数的概念
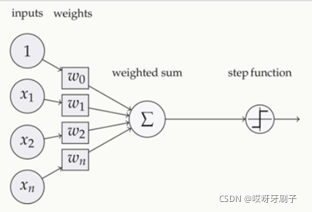
神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值,并将输入值传递给下一层。在多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,这个函数称为激活函数(又称激励函数)。以一个简单的全连接神经网络为例,上一层输出的结果会乘以权重后输入到这一层的每个节点中,而这一层的每个节点会将输入经过激活函数后向下传递。
激活函数对于人工神经网络理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如果没有激活函数,则神经网络就是很多线性家和的叠加,其非线性拟合性能会有很大的限制。
- 常见激活函数
2.1 Sigmoid函数
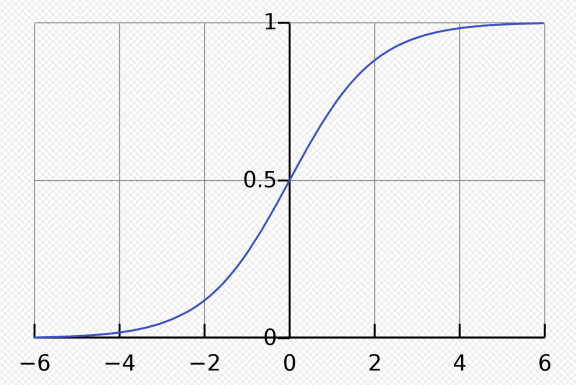
Sigmoid 是常用的非线性的激活函数,它的数学形式如下:
Sigmoid的几何图像如下:
它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1。这个性质使得sigmoid可以将输入的任何结果映射到0-1之间,实现归一化的效果,然而这种映射有可能会丢失一部分的输入信息。
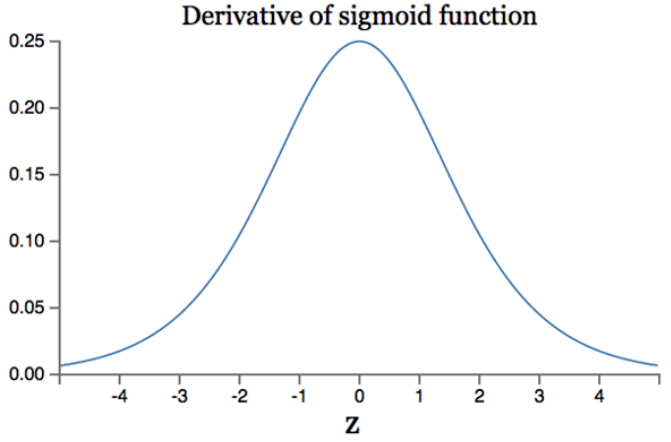
然而,sigmoid函数曾经被使用的很多,不过近年来,用它的人越来越少了。其主要的问题是在深度神经网络中梯度反向传递时导致梯度消失的问题,由sigmoid的导数函数:
如果我们初始化神经网络的权值为[0 , 1]之间的随机值,由反向传播算法的数学推导可知,梯度从后向前传播时,每传递一层梯度值都会减小为原来的0.25倍,如果神经网络隐层特别多,那么梯度在穿过多层后将变得非常小接近于0,即出现梯度消失现象;当网络权值初始化为(1 , +∞)区间内的值,则会出现梯度爆炸情况。
梯度消失将导致神经网络收敛速度缓慢,而梯度爆炸则会造成训练困难。
2.1 tanh函数
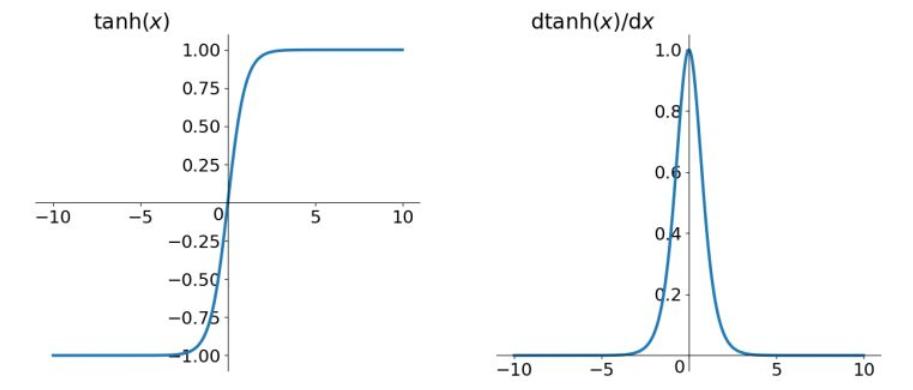
tanh函数解析式:
tanh函数及其导数的几何图像如下图:
tanh读作Hyperbolic Tangent,它解决了Sigmoid函数的不是0中心函数的问题,然而,梯度消失的问题和幂运算开销大的问题仍然存在。是人工神经网络早期对于sigmoid函数的一种优化形式。
2.3 Relu函数
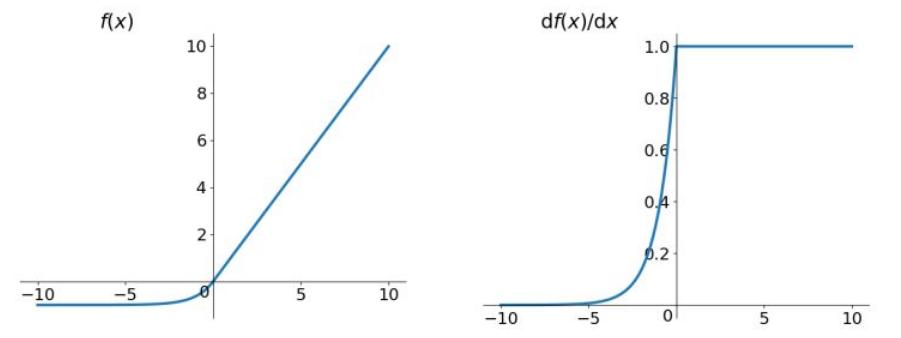
Relu函数的解析式:
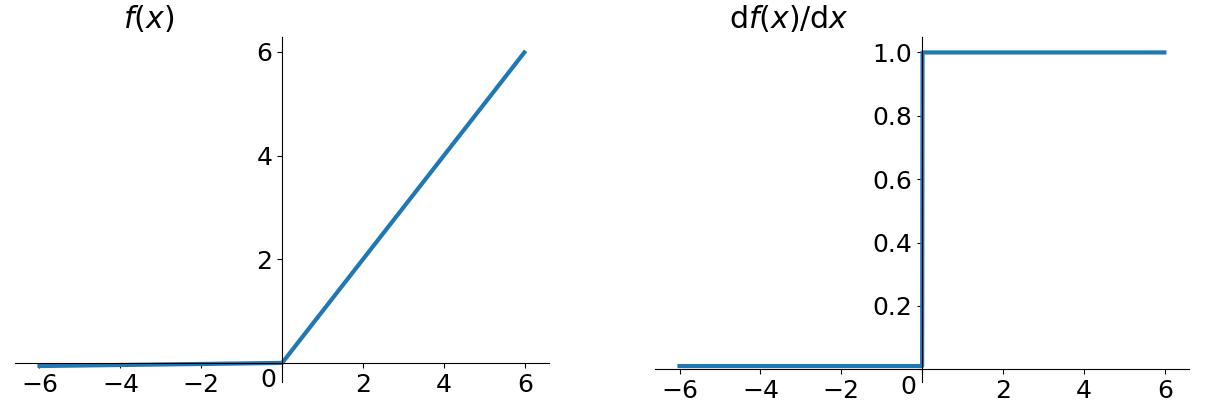
Relu函数及其导数的图像如下图所示:
Relu函数其实就是一个取最大值函数,这样一个简单的函数形式使得使用Relu作为激活函数的收敛和训练速度远快于sigmoid很tanh。一个直观的问题是它并不是全区间可导的,但是我们可以取区间导数,如右图所示。与前面提到的两种激活函数不同的是,这种导数形式尤其适合深度神经网络的情况,因为它在正区间内不存在梯度消失的问题。
然而Relu的输出不是zero-centered,并且存在Dead ReLU Problem,指的是某些神经元可能永远不会被激活,导致相应的参数永远不能被更新。从线性到非线性映射的角度上考虑,Relu是有些不足的,然而其应用的深度神经网络的情形很大程度上弥补了这个问题,更多的层数带来了更好更细致的拟合结果。
Relu目前是最常用的激活函数。
2.4 Leaky ReLU函数(PReLU)
函数表达式:
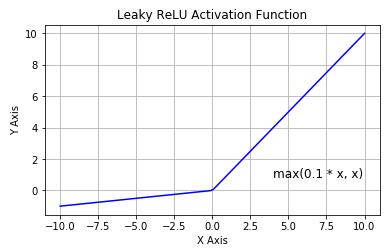
Leaky Relu函数的图像如下图所示:
与Relu差不多的表达式说明,Leaky Relu是以一种补充或者说优化Relu的身份出现的。人们为了解决Dead ReLU Problem,提出了将ReLU的前半段设为超参数α乘以x而非0,通常 α = 0.01。
理论上来讲,Leaky Relu应该有Relu的所有优点,外加不会有Dead ReLU问题,但是在实际操作当中,并没有完全证明Leaky Relu总是好于Relu。
2.5 ELU (Exponential Linear Units) 函数
函数表达式:
函数及其导数的图像如下图所示:
ELU也是为解决Relu存在的问题而提出,类似于Leaky Relu论上虽然好于Relu,实际使用中目前也没有发现ELU总是优于Relu。Relu目前依然是使用最多的激活函数,特别是在神经网络层数越来越多的情况下。