第一章 绪论

1.1 人工智能

人工智能的一个子领域

• 神经网络：一种以（人工）神经元为基本单元的模型
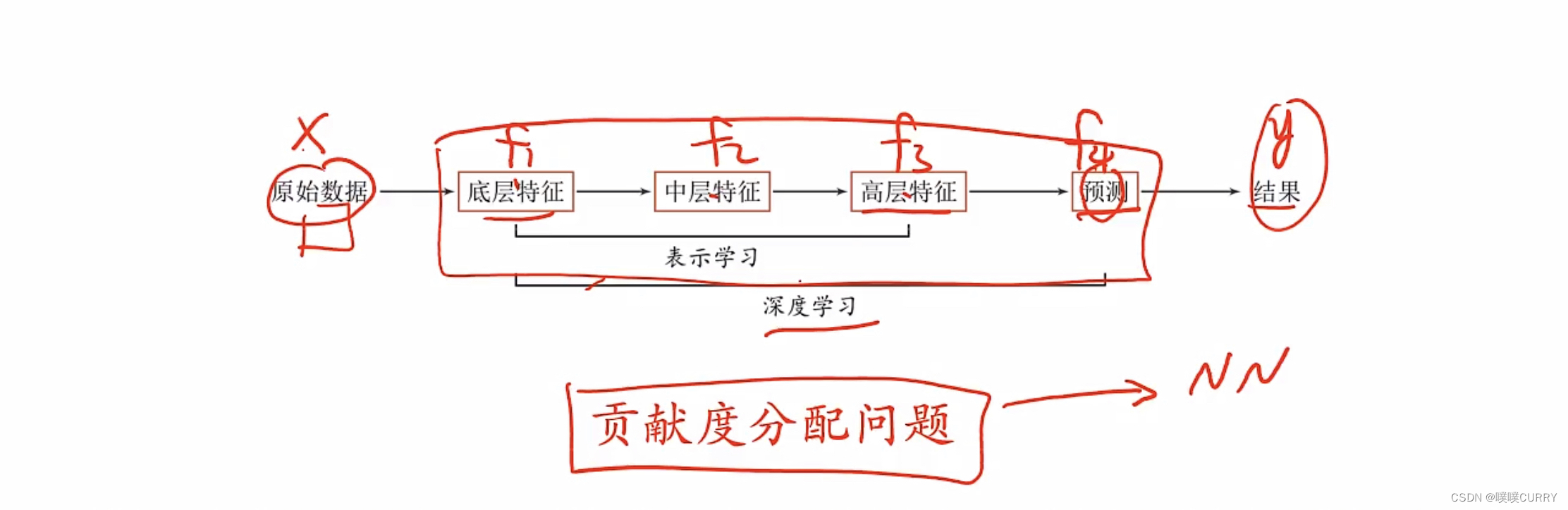
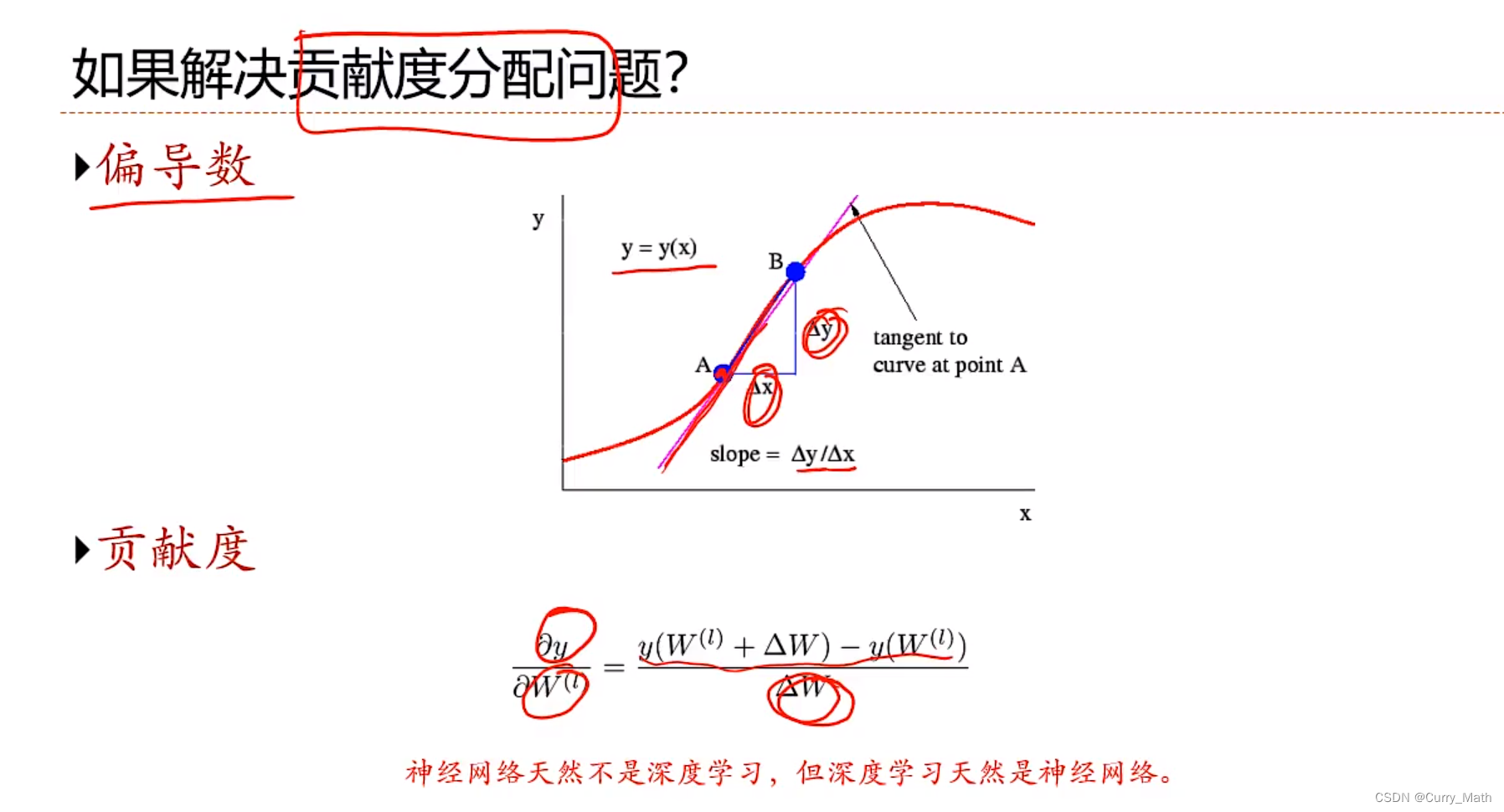
• 深度学习：一种机器学习问题，主要解决贡献度分配问题

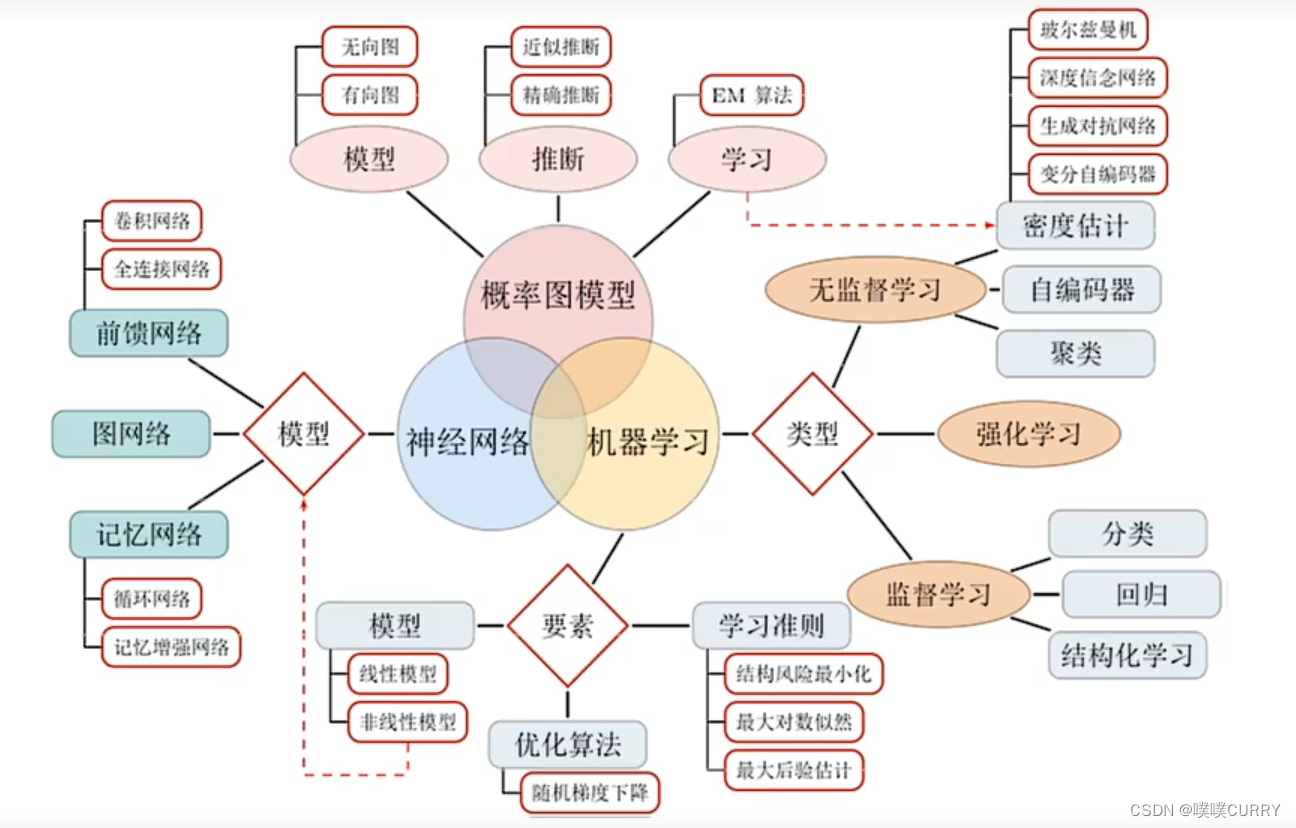
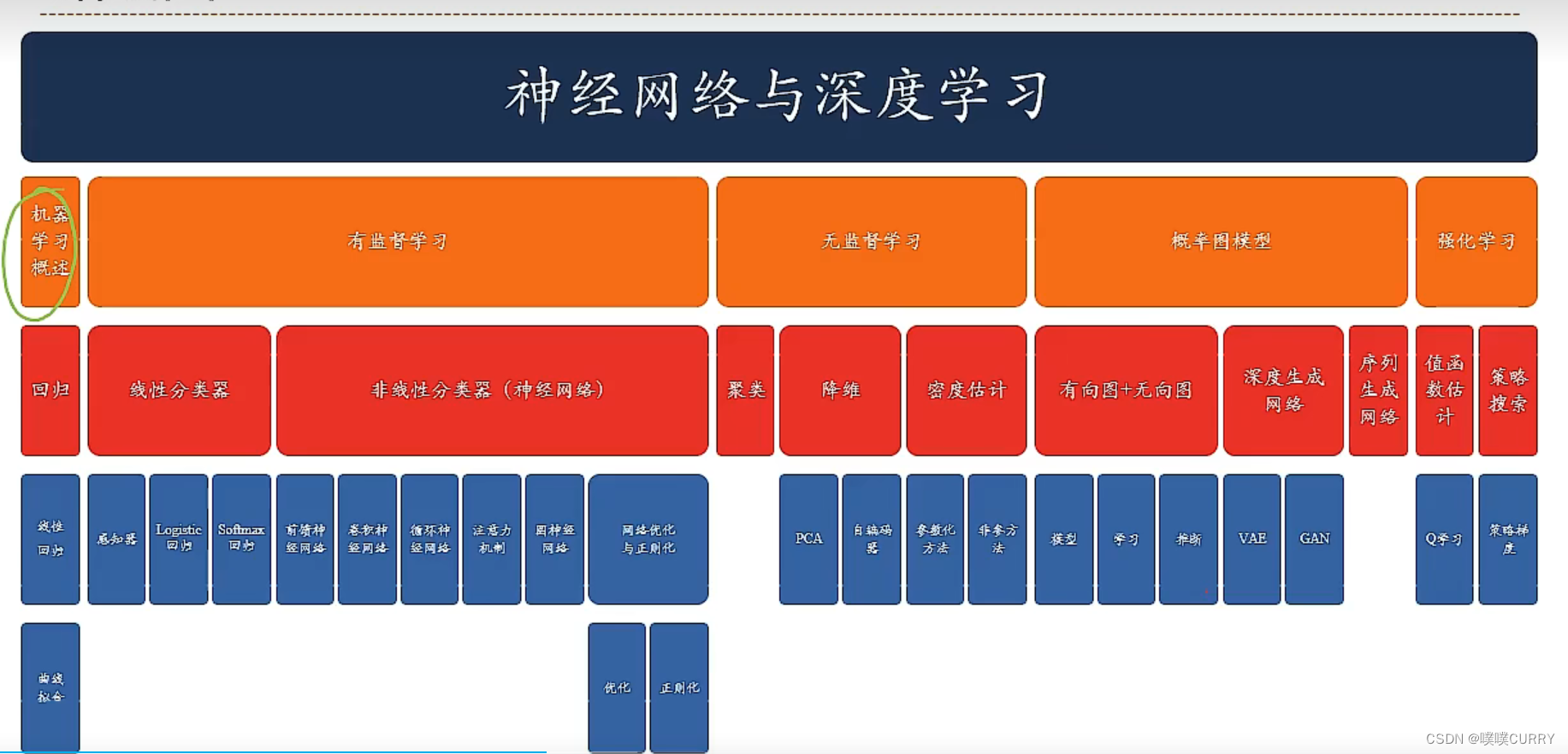
知识结构

知识结构图

路线图

预备知识

• 线性代数
• 微积分
• 数学优化
• 概率论
• 信息论

顶会论文

• NeurIPS、ICLR、ICML、AAAL、IJCAL
• ACL、EMNLP
• CVPR、ICCV

常用的深度学习框架

• 简易快速的原型设计
• 自动梯度计算
• 无缝CPU和GPU切换
• 分布式计算
• PYTORCH、TensorFlow

研究领域

• 机器感知（计算机视觉、语音信息处理、模式识别）
• 学习（机器学习、强化学习）
• 语言（自然语言处理）
• 记忆（知识表示）
• 决策（规划、数据挖掘）

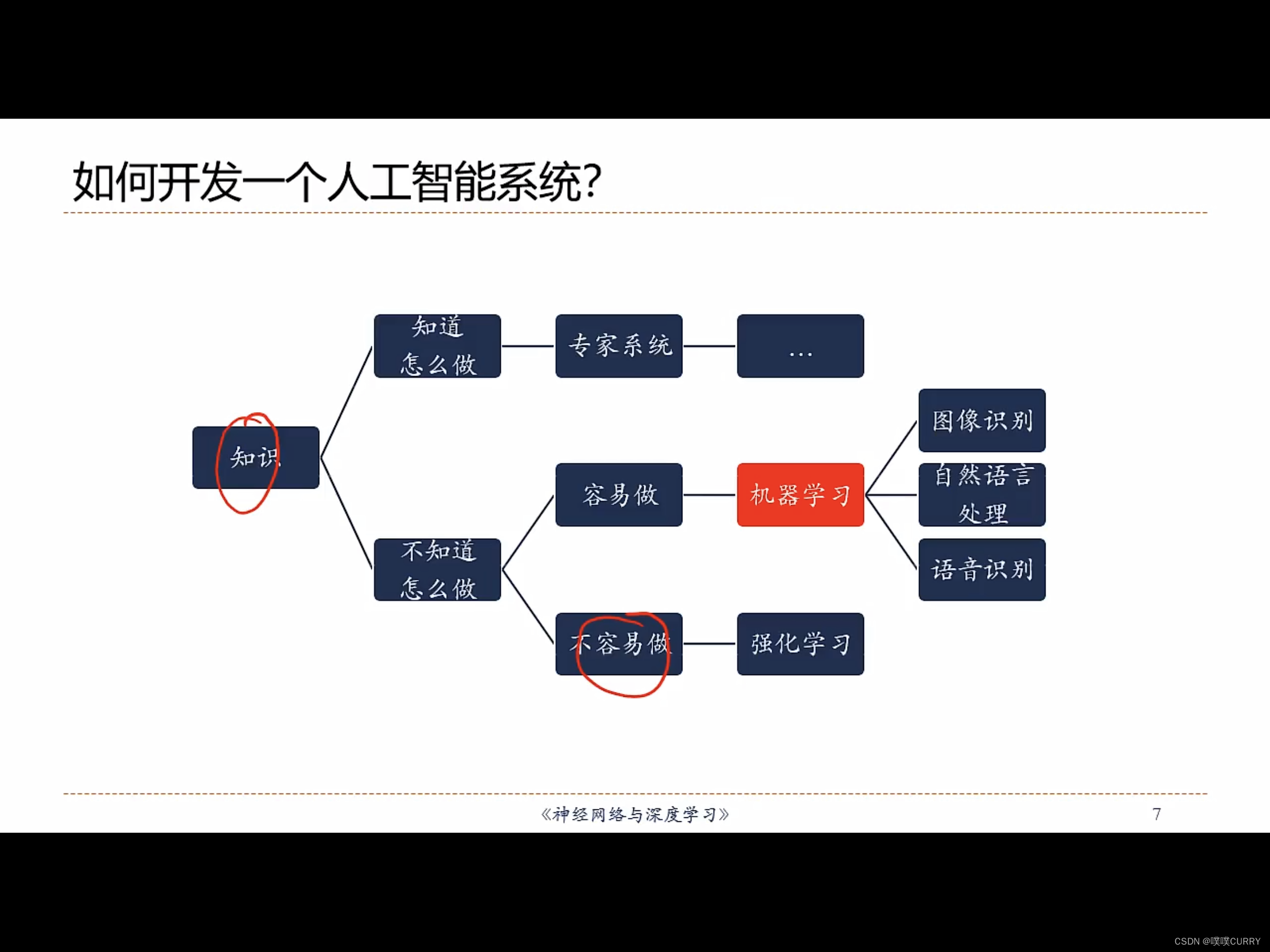
1.2 如何开发AIS

学习规则（rule）
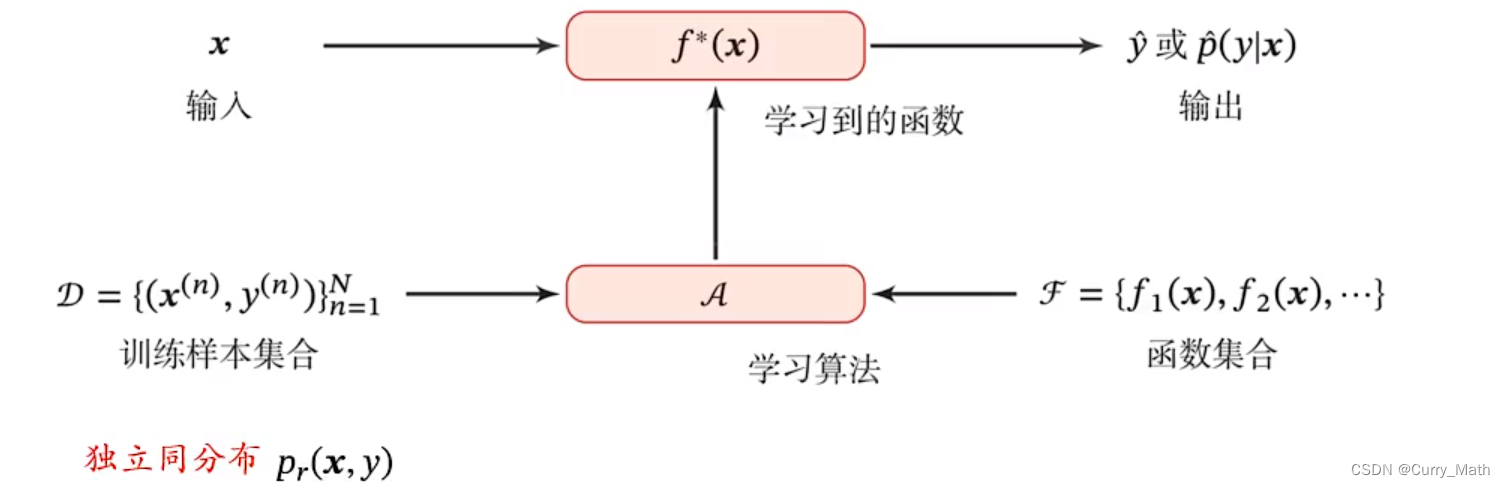
机器学习=构建一个映射函数

芒果机器学习

• 准备数据
• 学习（相关性模型）
• 测试

1.3 表示学习

机器学习的一般流程：

语义鸿沟:AI的挑战之一

• 底层特征VS高层语义
• 核心问题：“什么是一个好的表示”，“如何学习好的表示”
• 特征提取：基于任务或先验对去除无用特征
• 表示学习：通过深度模型学习高层语义特征

局部表示和分布式表示

• 局部表示:离散表示、符号表示
• 分布式表示：压缩、低维、稠密向量

1.4 深度学习（Deep Learning)

深度学习=表示学习+决策（预测）学习

深度学习的数学描述

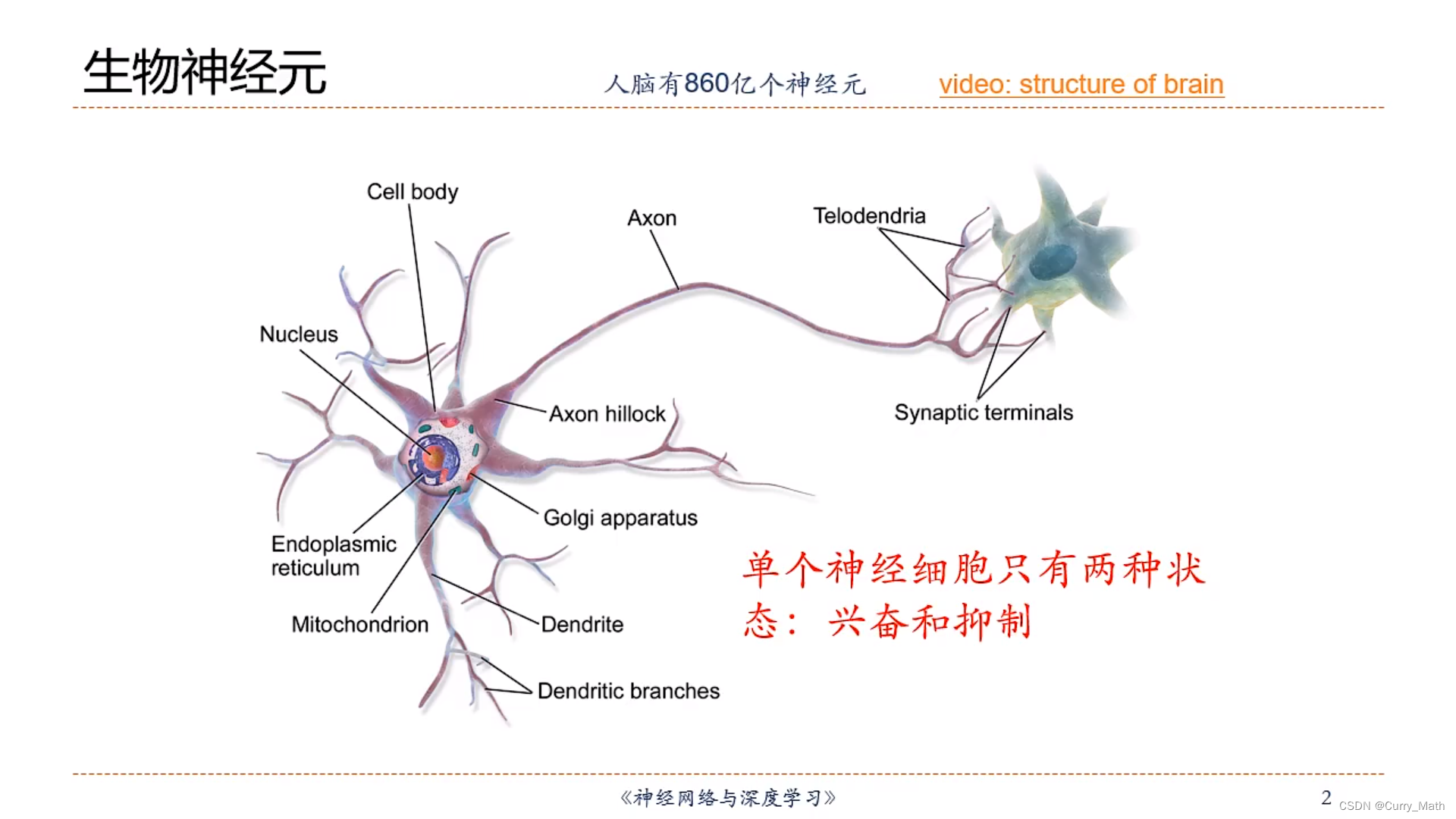
1.5 人脑神经网络

人类大脑是人体最复杂的器官，由神经元、神经胶质细胞、神经干细胞和血管组成。

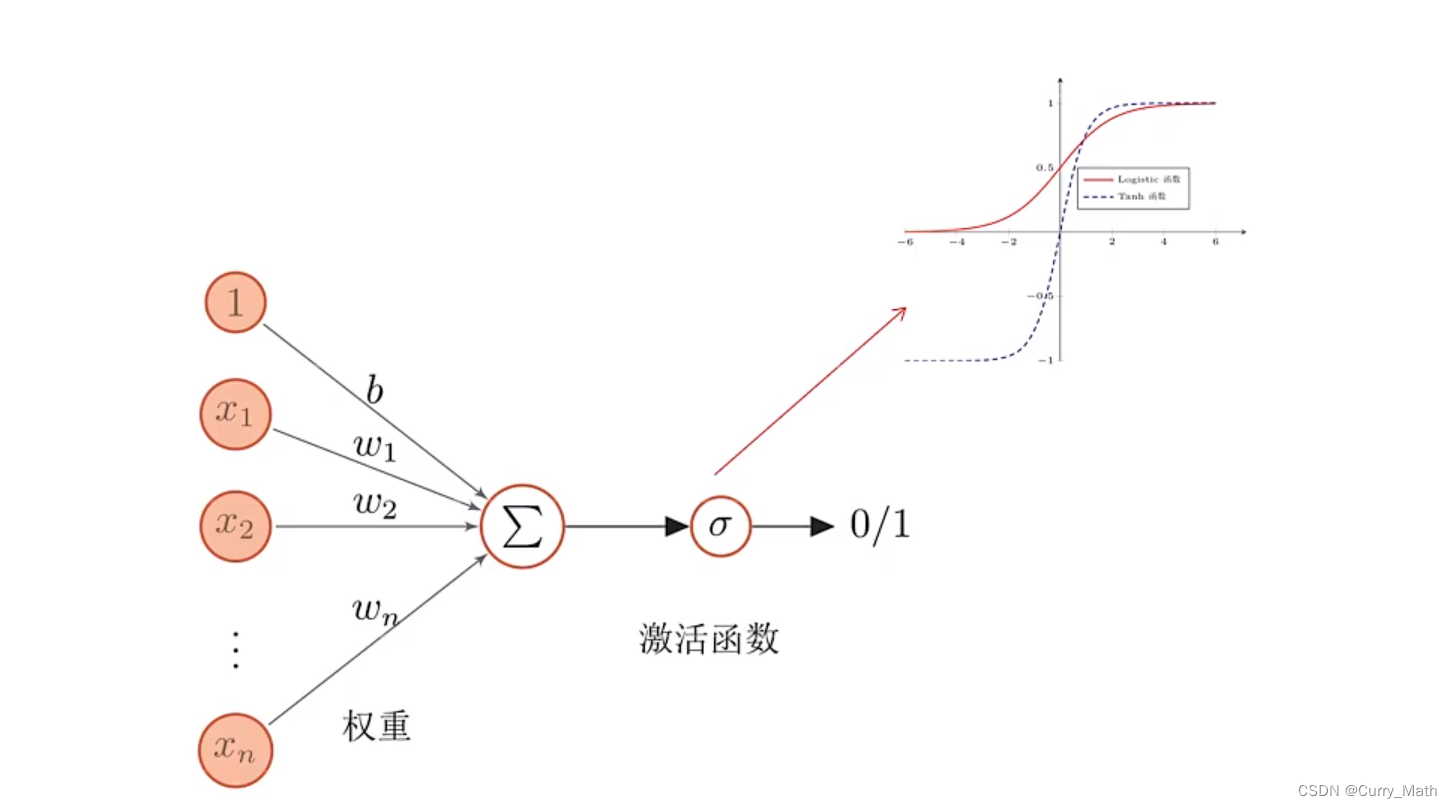
那么如何构造一个人工神经元呢？为此我们建立数学模型如下：

这里不同节点之间的连接被赋予了不同的权重，每个权重代表了一个节点对另一个节点的影响大小。每个节点代表一种特定函数，来自其他节点的信息经过其相对应的权重综合计算，输入到一个激活函数中并得到一个新的活性值（兴奋或者抑制）。从系统观点来看，，人工神经元网络是由大量神经元通过极其丰富和完善的连接而构成的自适应非线性动态系统。

人工神经网络

人工神经网络主要由大量的神经元以及它们之间的有线连接构成。因此考虑三方面：

• 神经元的激活规则：主要是指神经元输入到输出之间的映射关系，一般为非线性函数。
• 网络的拓扑结构：不同神经元之间的连接关系。
• 学习算法：通过训练数据来学习神经网络的参数。

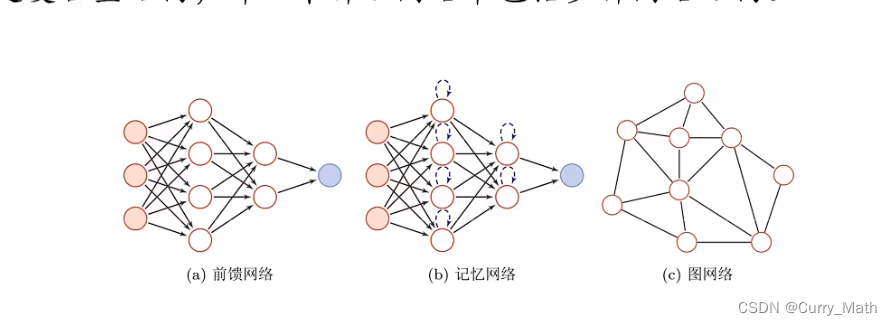
虽然将神经网络结构大体分为三种类型，但是·大多数网络都是复合型结构。即一个神经网络包括多种网络结构。

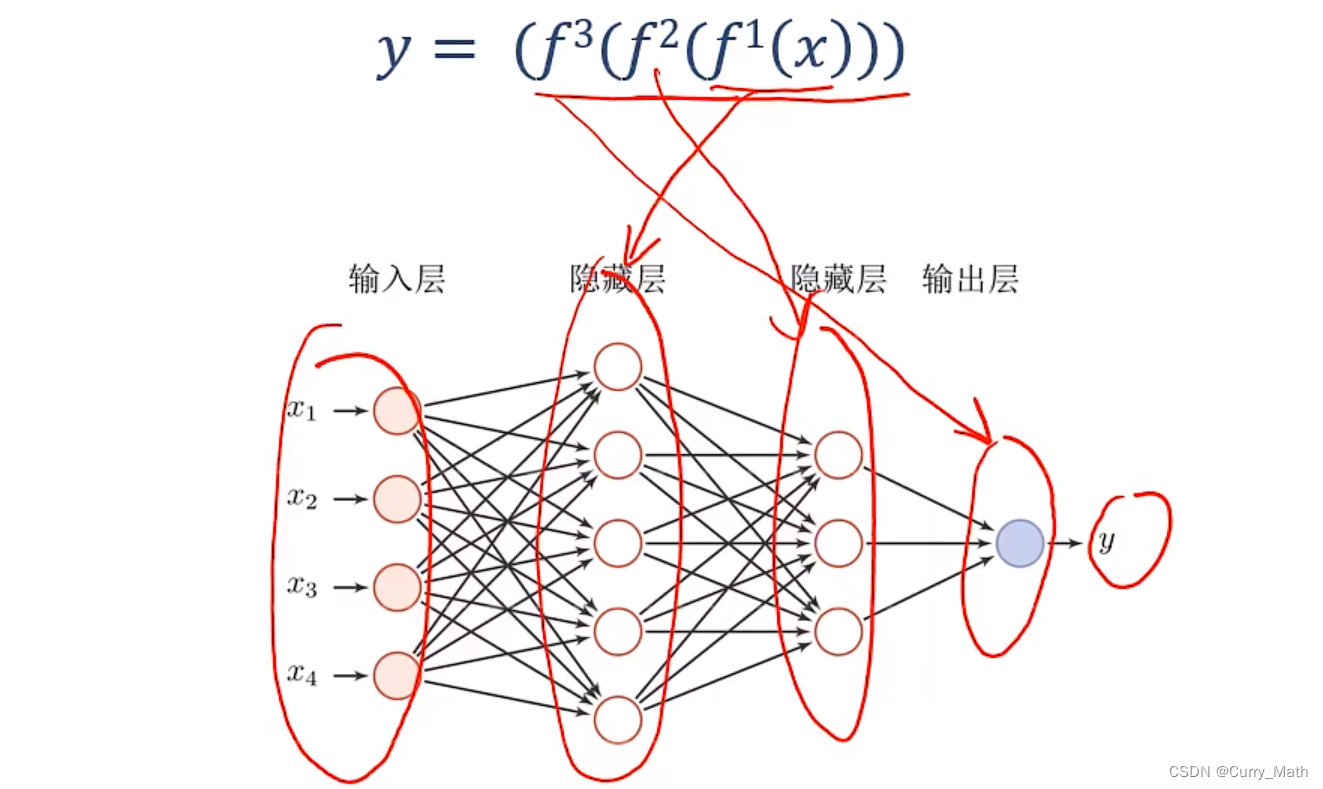
神经网络与深度学习之间的对应关系（隐藏层=f）

那么如何解决贡献度分配问题？

神经网络发展史

五个阶段

• 第一阶段：模型提出
• 第二阶段：冰河期
• 第三阶段：反向传播算法引起的复兴
• 第四阶段：流行度降低
• 第五阶段：深度学习的兴起

第二章 机器学习概述

2.1 基本概念

一些概率论的知识，此处略过。

2.2 机器学习定义

机器学习：通过算法使得机器能从大量数据中学习规律从而对新的样本做决策。
规律：决策（预测）函数

2.3 机器学习类型

回归（Regression)问题:电影票房预测，股价预测，房价预测
分类（Classification)问题:手写数字识别，人脸检测（Face Detection）,垃圾邮件检测（Spam Detection）
聚类问题：图像聚类（Clustering Images）
强化学习：AlphaGo，不断试错
典型的监督学习问题：回归、分类
无监督学习问题：聚类、降维、密度估计
总结：常见的机器学习类型

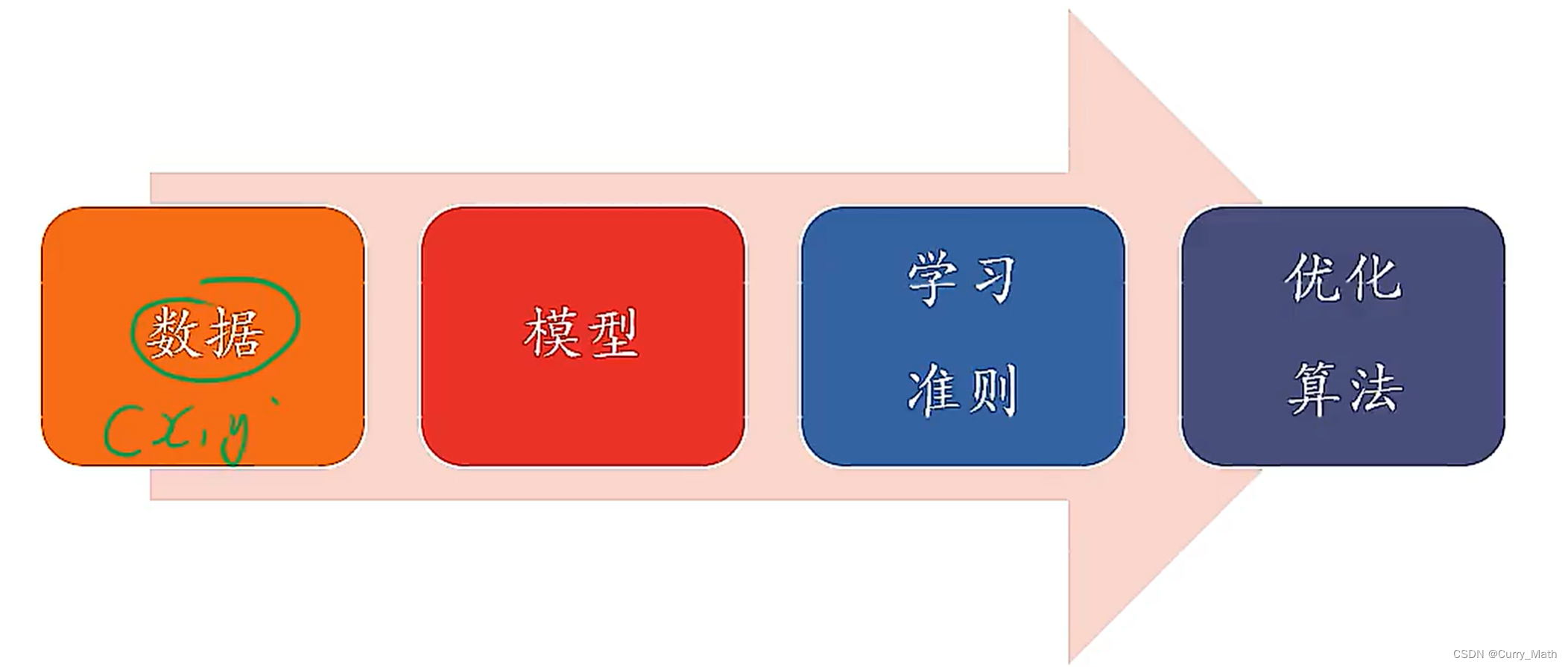
2.4 机器学习的要素

四个要素：数据、模型、学习准则、优化算法

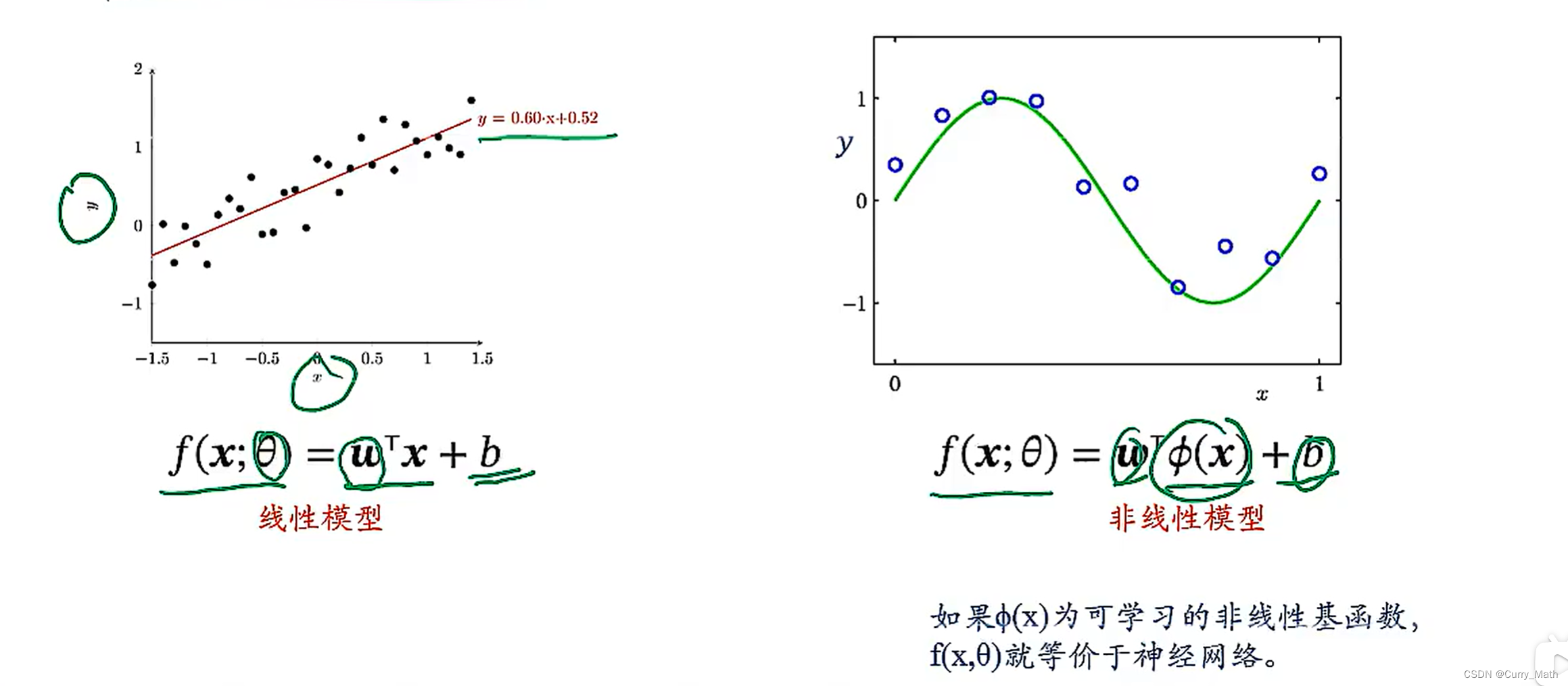
2.4.1 模型

• 回归（Regression）

2.4.2 学习准则

• 一个好的模型应该在所有取值上都与真实映射函数一致
  $\left|f\left(\mathbf{x},{\theta }^{\ast }\right)-y\right|<\epsilon ,\forall (\mathbf{x},y)\in X\times y$

• 损失函数（Loss Function）：损失函数是一个非负实数函数，用来量化模型预测和真实标签之间的差异

• 以回归问题为例
  -平方损失函数（Quadratic Loss Function)
  $\mathcal{L}(y,f(\mathbf{x};\theta ))=\frac{1}{2}(y-f(\mathbf{x};\theta ){)}^2$

• 期望风险：可以近似为
  训练数据：$:{\left\{\left({\mathbf{x}}^{(n)},y^{(n)}\right)\right\}}_{n=1}^N$
  经验风险：${\mathcal{R}}_{\mathcal{D}}^{emp}(\theta )=\frac{1}{N}{\sum }_{n=1}^N\mathcal{L}\left(y^{(n)},f\left({\mathbf{x}}^{(n)};\theta \right)\right)$
  经验风险最小化：寻找一个参数${\theta }^{\ast }$，使得风险函数最小化
  ${\theta }^{\ast }=\underset{\theta }{\mathrm{argmin}}{\mathcal{R}}_{\mathcal{D}}^{emp}(\theta )$
  机器学习问题转化为一个最优化问题！

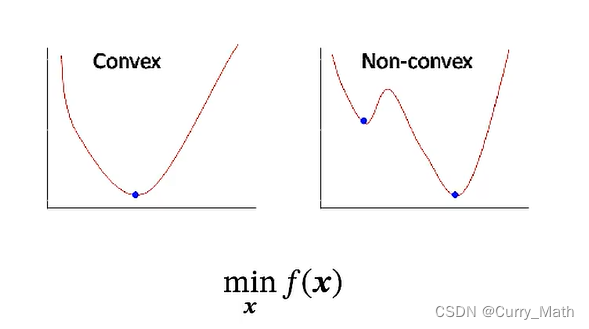
• 最优化问题
  
  凸优化：极值点处有极值；
  非凸优化问题：较为困难，使用一些优化算法.

2.4.3 优化算法

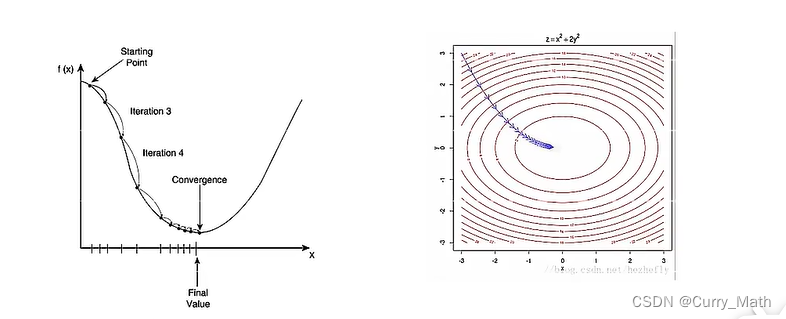
• 梯度下降法（Gradient Descent）
  

在机器学习中，最简单、最常用的优化算法就是梯度下降法。即首先初始化参数 $\theta$ ,然后按照下面的迭代方式来计算训练集$\mathcal{D}$上风险函数的最小值：
$\begin{array}{rl}{\theta }_{t+1}& ={\theta }_t-\alpha \frac{\partial {\mathcal{R}}_{\mathcal{D}}(\theta )}{\partial \theta }\\ & ={\theta }_t-\alpha \frac{1}{N}\sum _{n=1}^N\frac{\partial \mathcal{L}\left(y^{(n)},f\left({\mathbf{x}}^{(n)};\theta \right)\right)}{\partial \theta },\end{array}$

其中${\theta }_t$为第$t$次迭代时的参数值，$\alpha$为搜素步长.在机器学习中，$\alpha$一般称为学习率（Learning Rate)

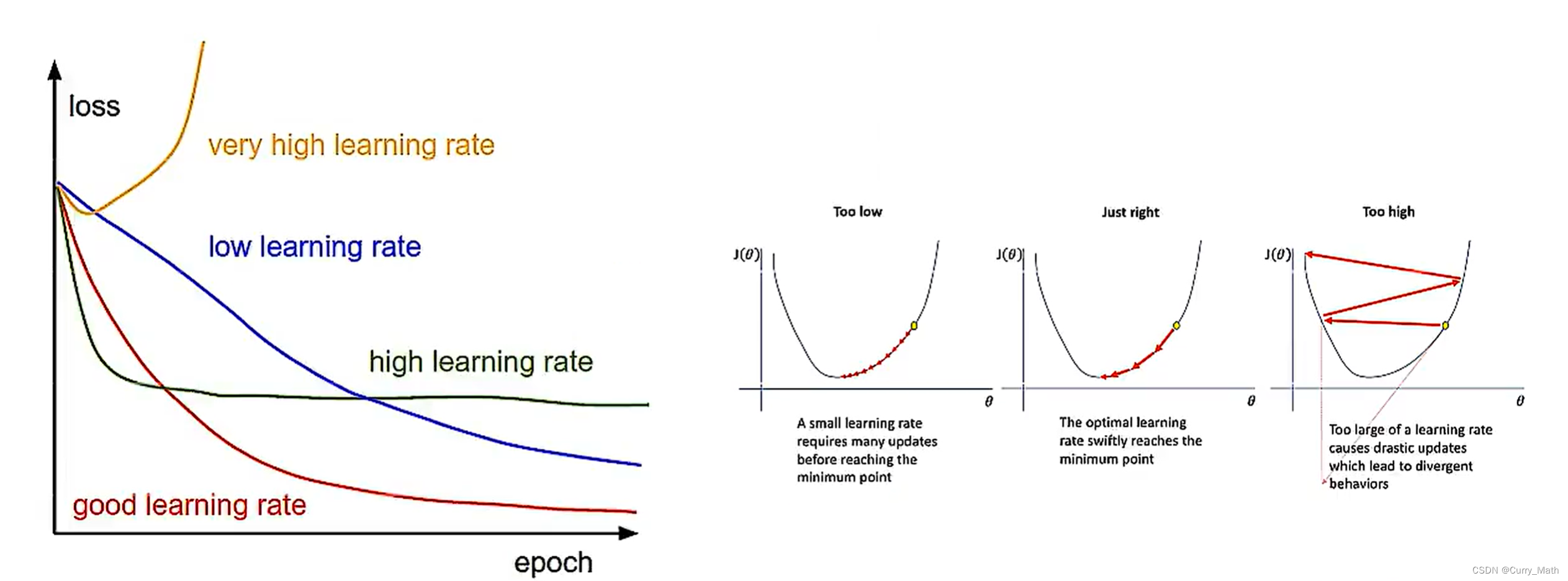
学习率是十分重要的超参数！

如果学习率太大，如最右边的图。在优化过程中，会跨越最低点，导致无法准确找到最值点。
如果学习率太小，损失下降比较慢，学习效率较低。
比较期望中间的学习率，叫做自适应学习率。

• 随机梯度下降法（SGD)

在机器学习中，我们假设每个样本都是独立同分布地从真实数据分布中随机抽取出来的，真正的优化目标是期望风险最小。批量梯度下降法相当于是从真实数据中采集N个样本，并由它们计算出来的经验风险的梯度来近似期望风险的梯度，为了减少每次迭代的计算复杂度，我们也可以在每次迭代是只采集一个样本，计算这个样本损失函数的梯度并更新参数。即随机梯度下降法。当经过族规次数的迭代时，随机梯度下降也可以收敛到局部最优解。

随机梯度下降法的训练过程如下面的算法所示：

优点：每次计算开销小，支持在线学习
缺点：无法充分利用计算机的并行计算能力

• 小批量随机梯度下降法

小批量梯度下降法是批量梯度下降和随机梯度下降的这种.每次迭代时，我们随机选取一部分训练样本来计算梯度并更新参数，这样既可以兼顾随机梯度下降法的优点，也可以提高训练效率。

第t次迭代时，随机选取一个包含K个样本的子集$S_t$，计算这个子集上每个样本损失函数的梯度并进行平均，然后再进行参数更新：
${\theta }_{t+1}\leftarrow {\theta }_t-\alpha \frac{1}{K}{\sum }_{(\mathbf{x},y)\in S_t}\frac{\partial \mathcal{L}(y,f(\mathbf{x};\theta ))}{\partial \theta }$.

在实际应用中，小批量随机梯度下降法有收敛快、计算开销小的优点，因此逐渐成为大规模机器学习中的主要优化算法。