前言

如何求解一个二进制中1的个数？有常规的O(N)法，还有基于分治的O(logN)，即Java的bitCount(int)方法。
对于bitCount(int)源码，是已经优化过的代码，已经看不到原始的分治逻辑，显的很难。但从分治原理到优化，思路非常简单，感受分治的魅力，感受挖掘规律进行优化的魅力。
所有的困难都是由简单知识点结合内部逻辑联系组合而成！

一、由易到难，头脑热身

如何求二进制中1的个数？常规的方法就是对每位二进制进行判定累计。

 	public int hammingWeight(int n) {
        int cnt = 0;
        for(int i = 0;i < 32;i++){
            if((1 << i & n) != 0) ++cnt;
        }
        return cnt;
    }

二、简单优化，一题多解

如果二进制计算基础，即常见位运算，那基本知道如何快速将最后一个1消掉。n - 1会导致二进制最后一个1被借用，其后的0全部变为1，如8 = 0x1000，8 - 1 = 7 = 0x0111； 那么n & (n - 1)就能把最后一个1消掉，如0x1000 & 0x0111 = 0x0000;

	public int hammingWeight(int n) {
        int cnt = 0;
        while(n != 0){
            ++cnt;

            n = n & (n - 1);
        }
        return cnt;
    }

这样就能减少判定次数，而且没有if判定。

三、分治优化

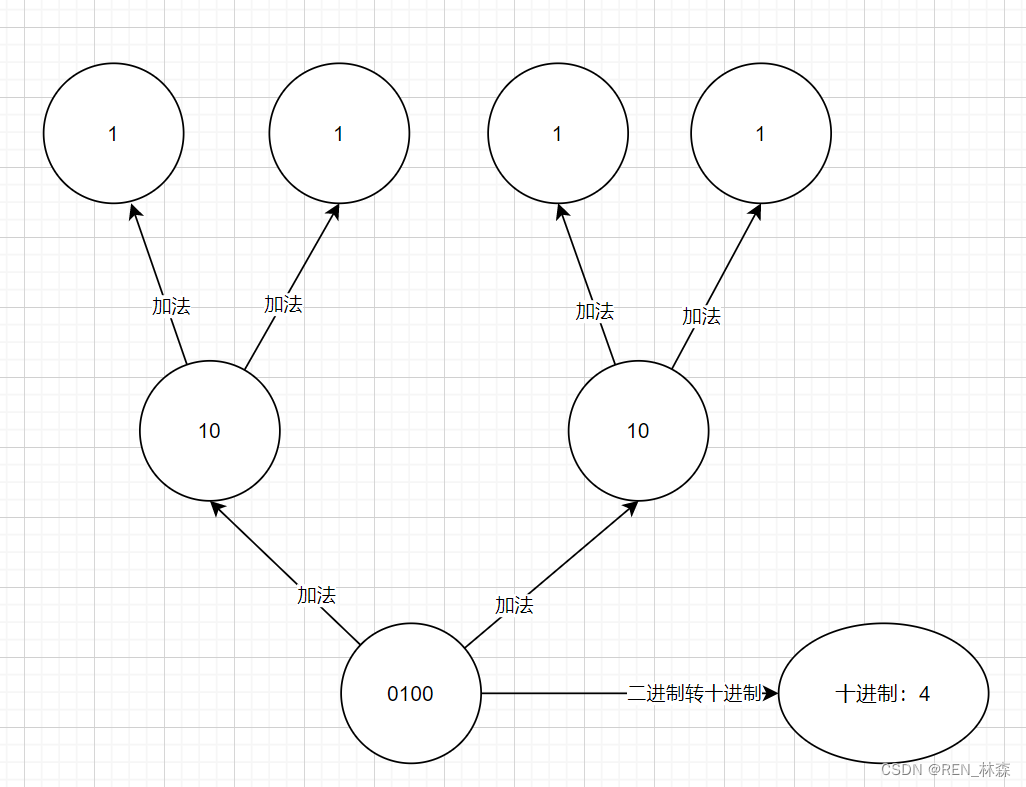
15 = 1111，如何分治计算1的个数，直接统计1的个数即可，即不断做加法即可。

提取关键问题，如何让前一位和后一位做加法呐？
直接将二进制无符号右移一位，前后两位不就对齐了吗？再用0101…来将左边多余的二进制抹除，再进行最终的加法运算。
0101 = 5，所以需要用5来抹除多余的1.

n = (n & 0x55555555) + ((n >>> 1) & 0x55555555);

统计了1位，接下来统计2位，再统计4位，继续统计8位 / 16位，都是同样的道理，直接通过无符号右移不同的位数进行加法统计即可。

public int hammingWeight(int n) {
		// 用0101来抹除多余的1 + 右移1位对齐。
        n = (n & 0x55555555) + ((n >>> 1) & 0x55555555);
        // 用0011来抹除多余的1 + 右移2位对齐。
        n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
        // 用00001111来抹除多余的1 + 右移4位对齐。
        n = (n & 0x0f0f0f0f) + ((n >>> 4) & 0x0f0f0f0f);
        // 用0000000011111111来抹除多余的1 + 右移8位对齐。
        n = (n & 0x00ff00ff) + ((n >>> 8) & 0x00ff00ff);
        // 用00000000000000001111111111111111来抹除多余的1 + 右移16位对齐。
        n = (n & 0x0000ffff) + ((n >> 16) & 0x0000ffff);
        
        return n;
    }

四、bitCount(int)源码优化

上面就是bitCount的分治原理，再深入挖掘二进制的规律，挖掘计算中的个性，来做一个优化。

1. 用0101来抹除多余的1 + 右移1位对齐。
   n = (n & 0x55555555) + ((n >>> 1) & 0x55555555);
   对于两位二进制来讲，0x11 - 0x01 = 0x10 = 2，表示有2个1，0x10 - 0x01 = 0x01 = 1表示有1位二进制，就是这么巧！
   注：0x11 >>> 1 = 0x01;0x10 >>> 1 = 0x01;
   对于第2为为0的情况，自然不用管，毕竟0x01 - 0x00 = 1;0x00 - 0x00 = 0;
   所以可以用减法，少一次与运算，n = n - ((n >>> 1) & 0x55555555)

2. 用0011来抹除多余的1 + 右移2位对齐。
   n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
   无法优化，没有二进制规律，而且最多4个1需要3位二进制表示。

3. 用00001111来抹除多余的1 + 右移4位对齐。
   n = (n & 0x0f0f0f0f) + ((n >>> 4) & 0x0f0f0f0f);
   这里需要统计的是1byte中1的个数，而1的个数最多有8个，4位二进制完全够用了，所以可以先做加法运行，再对多余的0进行抹除，来减少一次运算。即n = (n + (n >>> 4)) & 0x0f0f0f0f;

第4/5点同理，但是从第4点开始，就有8位的空间来统计二进制数，而int只有32位，只需6个bit可以完成统计，所以可进一步优化！
先不管多余的二进制（未对齐的错误运算），最后统一把其抹除，只用6bit即可，所以用0x111111 = 0x3f来抹除多余的二进制。

疑问：为什么4位时不行？而8/16位可以呐？还是回归到6bit足够表示32位二进制个数了，4bit不行，下次运算时，紧挨着的2bit被运算，而且还抹不掉这个未对齐的错误运算！

bitCount源码，即最终优化过的代码，

/**
     * Returns the number of one-bits in the two's complement binary
     * representation of the specified {@code int} value.  This function is
     * sometimes referred to as the <i>population count</i>.
     *
     * @param i the value whose bits are to be counted
     * @return the number of one-bits in the two's complement binary
     *     representation of the specified {@code int} value.
     * @since 1.5
     */
    @HotSpotIntrinsicCandidate
    public static int bitCount(int i) {
        // HD, Figure 5-2
        i = i - ((i >>> 1) & 0x55555555);
        i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
        i = (i + (i >>> 4)) & 0x0f0f0f0f;
        i = i + (i >>> 8);
        i = i + (i >>> 16);
        return i & 0x3f;
    }

总结

1）分治统计，从O(N)降到O(logN)。
2）从易到难，一步步挖掘内在规律和个性，一步步优化，完成经典之作。
3）所有困难都是由简单知识点和它们之间的内在逻辑联系构成！

参考文献

[1] LeetCode 位1的个数
[2] bitCount 源码解析
[3] JDK 12