文章目录
视频讲解
数据清洗
定义
对数据进行重新审查和校验,目的在于删除重复信息,纠正存在的错误,并提供数据的一致性
难点
数据针对的应用不同,难以归纳统一的方法和步骤,但可以根据不同的数据给出不同的数据清理方法
方法
- 解决缺失值:
平均值,最大值,最小值或更为复杂的概率估计代替缺失的值 - 去重
相等的记录合并为一条记录(即合并/清除) - 解决错误值
用统计分析的方法识别可能的错误值或异常值,如偏差分析、识别不遵守分布或回归方程的值,也可以用简单的规则库(常识性规则,业务特定规则等)检测数据值,或使用不同属性间的约束,外部的数据来检测和清理数据 - 解决数据的不一致性
比如数据是类别型或者次序型
场景
- 删除多列(pandas中的drop())
- 更改数据类型
- 将分类变量转换为数字变量
- 检查缺失数据
- 删除列中的字符串
- 删除列中的空格
- 用字符串连接两列(带条件)
- 转换时间戳(从字符串到日期时间格式)
数据处理
定义
对数据(数值/非数值)进行分析和加工的技术过程
总结
让数据能够更好的拟合模型,更便于计算,减少计算量(需要具体问题具体分析)
方法
- 对数变换
- 标准缩放
- 转换数据类型
- 独热编码(One-hot)
- 标签编码(Label)
打卡作业
作业问题
- 读取文件,显示后五行
- pandas中的两种数据结构
- pandas的可视化函数
- pearson系数为什么可以用来衡量数据之间的相关性
- 如何利用pandas来显示数据信息
作业回答
1. 读取文件
# 读取train文件
train = pd.read_csv("train.csv")
# 显示后五行,前五行为train.head()
train.tail()
2. 两种数据结构
- Series
Series是一种一维的存储数据的对象,由一组数据(Values)+数据标签(index)组成
并且数据和标签都可以自行定义,且可以不是数值(说白了数据和标签之间是映射关系)
# 可以放入一个数组,也可以指定索引
ser1 = pd.Series([1,2,3])
ser2 = pd.Series([1,2,3],index=['a','b','c']) #index参数默认为整数型,可修改
ser1 # 查看内容,一般是一列索引一列数据,下面是数据的类型
ser1.values # 查看数据
ser1.index # 查看索引(范围)
ser2['d'] = 4 # 添加一个数据和其索引
# 索引用法
'b' in ser2 # 查看b是否在ser2中,返回boolean类型
x = {'e': 100, 'f':101, 'g':102, 'h':103}
y = pd.Series(x) # 其他用法,将字典转换为Serises型
s = {'e', 'g', 'h'}
z = pd.Series(x, index=s)
y + z # Series会对其索引进行算术运算,没对齐的都是NaN
# 其他用法
x = {'e': 100, 'f':101, 'g':102}
ser3 = pd.Series(x) # 将字典转换为Serises型
# Series本身和索引都有name属性
ser3.name='mmp'
ser3.index.name='mmpo'
-
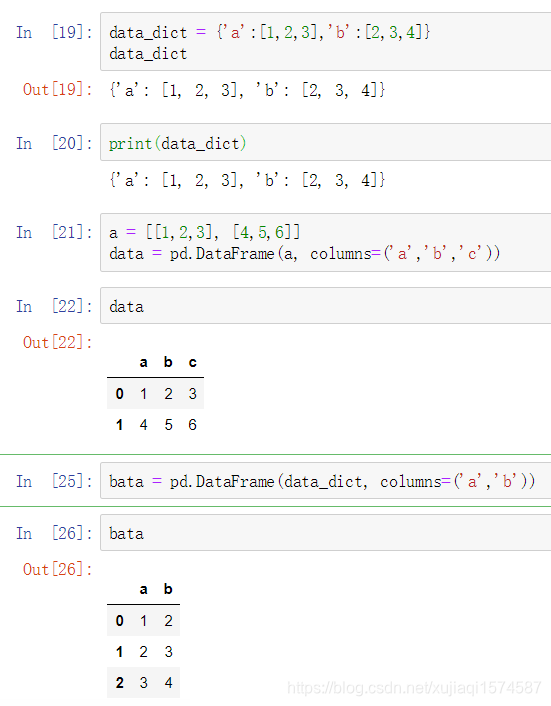
DataFrame
DataFrame是一种二维的存储数据的对象,它的索引有行(index)列(columns,相当于name)
3. pandas中的可视化函数
.plot()方法
plot()方法可以生成Series和DataFrame的线型图,DataFrame中还会自己创建图例
参数:
1. 线型图
None
2. 柱状图
kind='bar'垂直柱状图
kind='barh'水平柱状图
ax 指定在某个子图上作图
stacked=True 生成堆积柱状图
3. 密度图
kind='kde' 密度图
.hist()方法
对频率进行离散化,生成直方图
.scatter()方法
传入X, Y轴,生成散点图
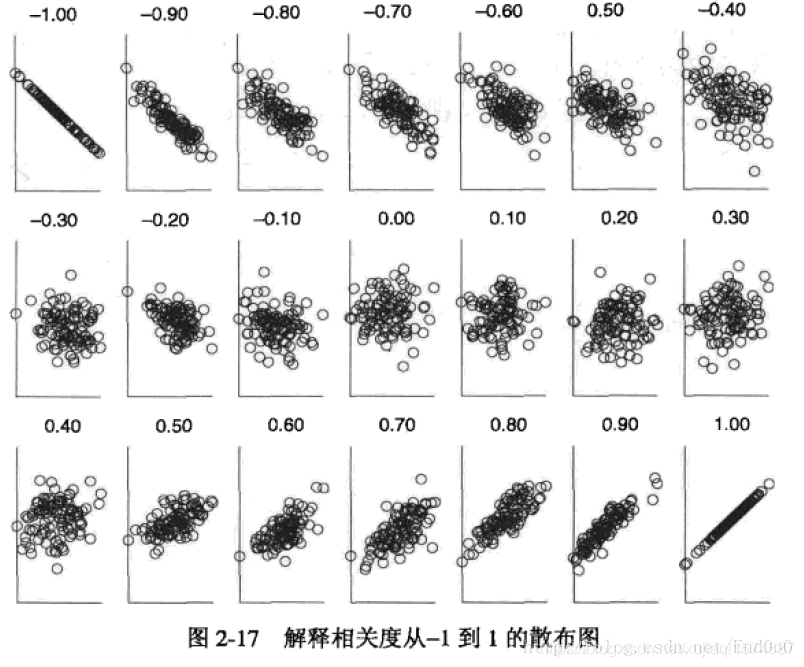
4. pearson系数为什么可以用来衡量数据之间的相关性
样本点估计pearson相关系数公式如下
r = 1 n − 1 ∑ i = 1 n ( X i − X ‾ σ X ) ( Y i − Y ‾ σ Y ) r=\frac{1}{n-1} \sum_{i=1}^{n}\left(\frac{X_{i}-\overline{X}}{\sigma_{X}}\right)\left(\frac{Y_{i}-\overline{Y}}{\sigma_{Y}}\right) r=n−11∑i=1n(σXXi−X)(σYYi−Y)
原公式就是二者协方差除以二者标准差之积
协方差是X,Y的值分别与其期望的差 的乘积的期望,衡量的是它们与平均值的距离的期望,反应了它们的正负相关,但是在数据比较分散的时候单纯的协方差并不能很好地反映X,Y的相关度,很多时候协方差看起来还是比较大,但实际相关度比较小,所以需要引入它们的标准差,标准差衡量的是它们的分散程度,两者的商就能平衡掉数据分散带来的影响
图引用自JasonCcccc博客 https://blog.csdn.net/ichuzhen/article/details/79535226
5. 如何利用pandas来显示数据信息
# 简单查看数据
dataframe.head()
# 数据维度
dataframe.shape
# 属性和类型
dataframe.dtypes
# 统计性描述
dataframe.describe()
# 数据分组分布
print(data.groupby('class').size())
# 数据属性相关性
print(data.corr(method='pearson'))
# pearson相关系数
dataframe.corr(method='pearson')
# 偏度
data.skew()
# 峰度
data.kurt()
引用自李威威博客 https://blog.csdn.net/lw_power/article/details/83180900