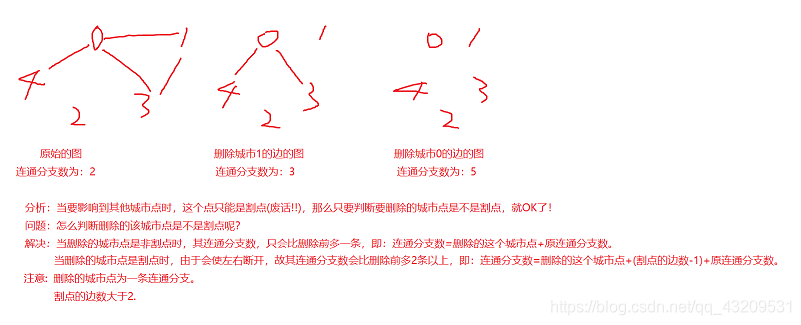
战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序，当失去一个城市导致国家被分裂为多个无法连通的区域时，就发出红色警报。注意：若该国本来就不完全连通，是分裂的k个区域，而失去一个城市并不改变其他城市之间的连通性，则不要发出警报。

输入格式：
输入在第一行给出两个整数N（0 < N ≤ 500）和M（≤ 5000），分别为城市个数（于是默认城市从0到N-1编号）和连接两城市的通路条数。随后M行，每行给出一条通路所连接的两个城市的编号，其间以1个空格分隔。在城市信息之后给出被攻占的信息，即一个正整数K和随后的K个被攻占的城市的编号。

注意：输入保证给出的被攻占的城市编号都是合法的且无重复，但并不保证给出的通路没有重复。

输出格式：
对每个被攻占的城市，如果它会改变整个国家的连通性，则输出Red Alert: City k is lost!，其中k是该城市的编号；否则只输出City k is lost.即可。如果该国失去了最后一个城市，则增加一行输出Game Over.。

输入样例：
5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3
输出样例：
City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.

注意点：

解答：

#include <cstdio>
#include <memory.h>

int map[501][501];
int N,oldLinkCount,newLinkCount,isVisit[501];

//	1初始化地图
void initMap();
//	2处理失去的城市
void dealLossCity();
//	3获得连通分支数
int goMap();
//	4遍历所有与其连通的城市
void linkedToEnd(int city);

int main() {
	initMap();
	dealLossCity();
	return 0;
}

/**
 * 	1初始化地图
 */
void initMap() {
	int M,x,y,i;
	scanf("%d %d",&N,&M);
	memset(map,0,sizeof(map));
	for(i=0; i<M; i++) {
		scanf("%d %d",&y,&x);
		map[y][x]=map[x][y]=1;
	}
	oldLinkCount = goMap();
}

/**
 * 	2处理失去的城市
 */
void dealLossCity() {
	int i,j,K,lossCity;
	scanf("%d",&K);
	for(i=0; i<K; i++) {

		scanf("%d",&lossCity);

		for(j=0; j<N; j++){
			map[lossCity][j]=map[j][lossCity]=0;
		}

		newLinkCount = goMap();

		//	如果删除边以后的地图连通分支数比删除前的多2,就要发出红色警报
		if(newLinkCount>=oldLinkCount+2) {
			printf("Red Alert: City %d is lost!\n",lossCity);
		}else {
			printf("City %d is lost.\n",lossCity);
		}
		oldLinkCount = newLinkCount;
		if(i==N-1) {
			printf("Game Over.\n");
		}
	}

}

/**
 * 	3获得连通分支数
 */
int goMap(){
	memset(isVisit,0,sizeof(isVisit));
	int count=0;
	for(int i=0; i<N; i++){
		if(isVisit[i]==0){
			linkedToEnd(i);
			count++;
		}
	}
	return count;
}

/**
 * 	4遍历所有与其连通的城市
 */
void linkedToEnd(int city) {
	isVisit[city]=1;
	for(int i=0; i<N; i++){
		if(isVisit[i]==0 && map[city][i]==1){
			linkedToEnd(i);
		}
	}
}