决策树原理
- ⚫决策树:从训练数据中学习得出一个树状结构的模型。
- ⚫决策树属于判别模型。
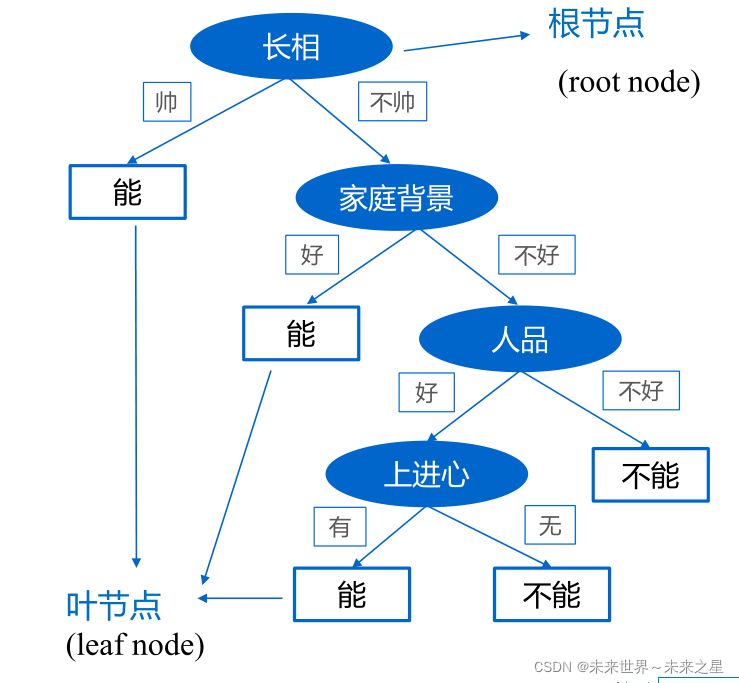
- ⚫决策树是一种树状结构,通过做出一系列决策(选择)来对数据进行划分,这类似于针对一系列问题进行选择。
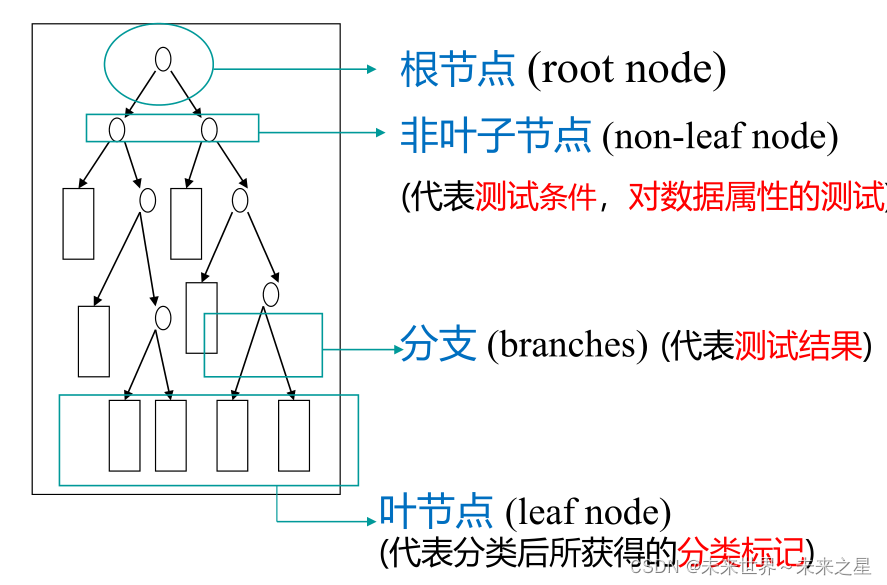
- ⚫决策树的决策过程就是从根节点开始,测试待分类项中对应的特征属性,并按照其值选择输出分支,直到叶子节点,将叶子节点的存放的类别作为决策结果。
- 决策树算法是一种归纳分类算法,它通过训练数据学习,挖掘出有用的规则**,用于对新数据进行预测**
- 决策树算法属于监督学习方法
- 决策树归纳的基本算法是贪心算法,自顶向下来构建决策树。
- 贪心算法:在每一步选择中都采取在当前状态下最好/最优的选择
- 在决策树的生成过程中,分割方法即属性选择的度量是关键
决策树的优缺点:
- 优点:
- 1.推理过程容易理解,计算简单,可解释性强。
- 2.比较合适处理有缺失值的样本
- 3.可自动忽略目标变量没有贡献的属性变量,也为判断属性变量的重要属性,减少变量的数目提供参考。
缺点:
- 1.容易造成过拟合,需要采用剪枝操作
- 2.忽略了数据之间的相关性
- 3.对于各类别样本数量不一致的数据,信息增益会偏向那些更多数值的特征。
-建立决策树的关键,即在当前状态下选择哪个属性作为分类依据。
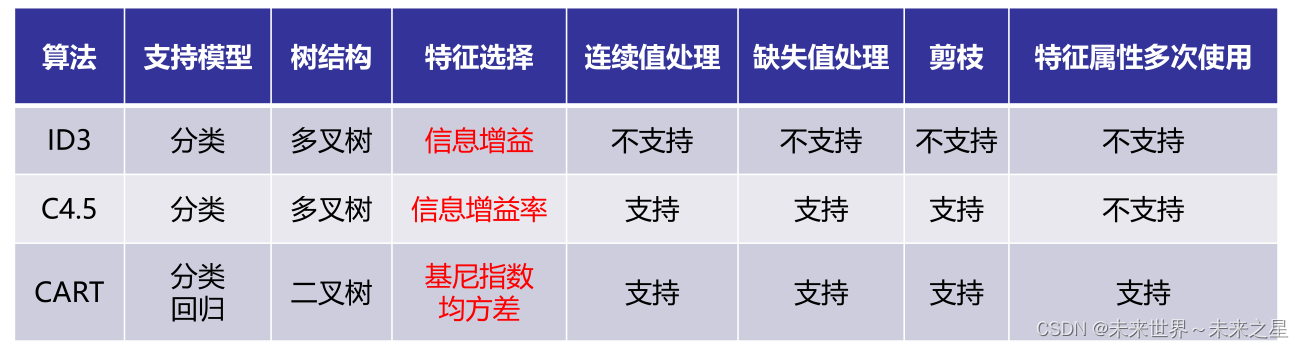
ID3算法
- ID3算法是以信息论为基础,以信息增益为衡量标准,从而实现对数据的归纳分类。
- ID3算法计算每个属性的信息增益,并选取具有最高增益的属性作为给定的测试属性
- ID3算法的步骤:
- 1.初始化特征集合核数据集合
- 2.计算数据集合信息熵和所有特征的条件熵,选择信息增益最大的特征作为当前决策节点
- 更新数据集合和特征集合(删除上一步使用的特征,并按照特征值来划分不同分支的数据集合)
- 4.重复2、3两步,若子集值包含单一特征,则为分支叶子节点。
信息熵: H ( D ) = − ∑ k = 1 k ∣ C k ∣ ∣ D ∣ l o g 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum^{k}_{k=1}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|} H(D)=−k=1∑k∣D∣∣Ck∣log2∣D∣∣Ck∣
K K K是类别,D是数据集, C k C_{k} Ck是类别 K K K下的数据集
下边的数据中:
| 数量 | 是 | 否 | 信息熵 |
|---|---|---|---|
| 15 | 9 | 6 | 0.971 |
H
(
D
)
=
−
∑
k
=
1
k
∣
C
k
∣
∣
D
∣
l
o
g
2
∣
C
k
∣
∣
D
∣
=
−
9
15
l
o
g
2
9
15
−
6
15
l
o
g
2
6
15
=
0.971
H(D)=-\sum^{k}_{k=1}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|}=-\frac{9}{15}log_{2}\frac{9}{15}-\frac{6}{15}log_{2}\frac{6}{15}=0.971
H(D)=−k=1∑k∣D∣∣Ck∣log2∣D∣∣Ck∣=−159log2159−156log2156=0.971
H
(
D
∣
A
1
=
中
年
)
=
−
∑
k
=
1
k
∣
C
k
∣
∣
D
∣
l
o
g
2
∣
C
k
∣
∣
D
∣
=
−
2
5
l
o
g
2
2
5
−
3
5
l
o
g
2
3
5
=
0.971
H(D|A_{1}=中年)=-\sum^{k}_{k=1}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|}=-\frac{2}{5}log_{2}\frac{2}{5}-\frac{3}{5}log_{2}\frac{3}{5}=0.971
H(D∣A1=中年)=−k=1∑k∣D∣∣Ck∣log2∣D∣∣Ck∣=−52log252−53log253=0.971
H
(
D
∣
A
1
=
老
年
)
=
−
∑
k
=
1
k
∣
C
k
∣
∣
D
∣
l
o
g
2
∣
C
k
∣
∣
D
∣
=
−
4
5
l
o
g
2
4
5
−
1
5
l
o
g
2
1
5
=
0.7219
H(D|A_{1}=老年)=-\sum^{k}_{k=1}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|}=-\frac{4}{5}log_{2}\frac{4}{5}-\frac{1}{5}log_{2}\frac{1}{5}=0.7219
H(D∣A1=老年)=−k=1∑k∣D∣∣Ck∣log2∣D∣∣Ck∣=−54log254−51log251=0.7219
信息增益
g
(
D
,
A
)
=
H
(
D
)
−
H
(
D
∣
A
)
g(D,A)=H(D)-H(D|A)
g(D,A)=H(D)−H(D∣A)其中,
H
(
D
∣
A
)
=
−
∑
i
=
1
n
∣
D
i
∣
∣
D
∣
l
o
g
2
∣
D
i
∣
∣
D
∣
H(D|A)=-\sum^{n}_{i=1}\frac{|D_{i}|}{|D|}log_{2}\frac{|D_{i}|}{|D|}
H(D∣A)=−∑i=1n∣D∣∣Di∣log2∣D∣∣Di∣,n是特征A的取值个数
ID3算法的缺点
- ID3没有剪枝策略,容易过拟合
- 信息增益准则对可取值数目较多的特征有所偏好,类似”编号“的特征,其信息增益接近于
- 只能用于处理离散分布的特征
- 没有考虑缺失值
C4.5算法
- 定义:
- C4.5算法是Ross对ID3算法的改进。
- ⚫用信息增益率来选择属性。ID3选择属性用的是子树的信息增益,
而C4.5用的是信息增益率。 - ⚫在决策树构造过程中进行剪枝。
- ⚫对非离散数据也能处理。
- ⚫能够对不完整数据进行处理。
- 信息增益
g R ( D , A ) = g ( D , A ) H A ( D ) g_{R}(D,A)=\frac{g(D,A)}{H_{A}(D)} gR(D,A)=HA(D)g(D,A),其中 H ( D ∣ A ) = − ∑ k = 1 k ∣ C k ∣ ∣ D ∣ l o g 2 ∣ C k ∣ ∣ D ∣ H(D|A)=-\sum^{k}_{k=1}\frac{|C_{k}|}{|D|}log_{2}\frac{|C_{k}|}{|D|} H(D∣A)=−∑k=1k∣D∣∣Ck∣log2∣D∣∣Ck∣
- 过拟合的原因:
- 为了尽可能正确分类训练样本,节点的划分过程会不断重复直到不能再分,这样就可能对训练样本学习的“太好”了,把训练样本的一些特点当做所有数据都具有的一般性质,从而导致过拟合。剪枝的基本策略有“预剪枝”(prepruning)和“后剪枝”(post-pruning)
- 通过剪枝处理去掉一些分支来降低过拟合的风险
- 预剪枝(prepruning)
- 预剪枝不仅可以降低过拟合的风险而且还可以减少训练时间,但另一方面它是基于“贪心”策略,会带来欠拟合风险。
- 主要方法有:
节点内数据样本低于某一阈值;
所有节点特征都已分裂;
节点划分前准确率比划分后准确率高。 - 后剪枝
- 在已经生成的决策树上进行剪枝,从而得到简化版的剪枝决策树。
- 后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情况下,后剪枝的欠拟合风险更小,泛化性能往往优于预剪枝决策树
优缺点: - 剪枝策略可以再优化;
- C4.5 用的是多叉树,用二叉树效率更高;
- C4.5 只能用于分类;
- C4.5 使用的熵模型拥有大量耗时的对数运算,连续值还有排序运算;
- C4.5 在构造树的过程中,对数值属性值需要按照其大小进行排序,从中选择一个分割点,所以只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时,程序无法运行。
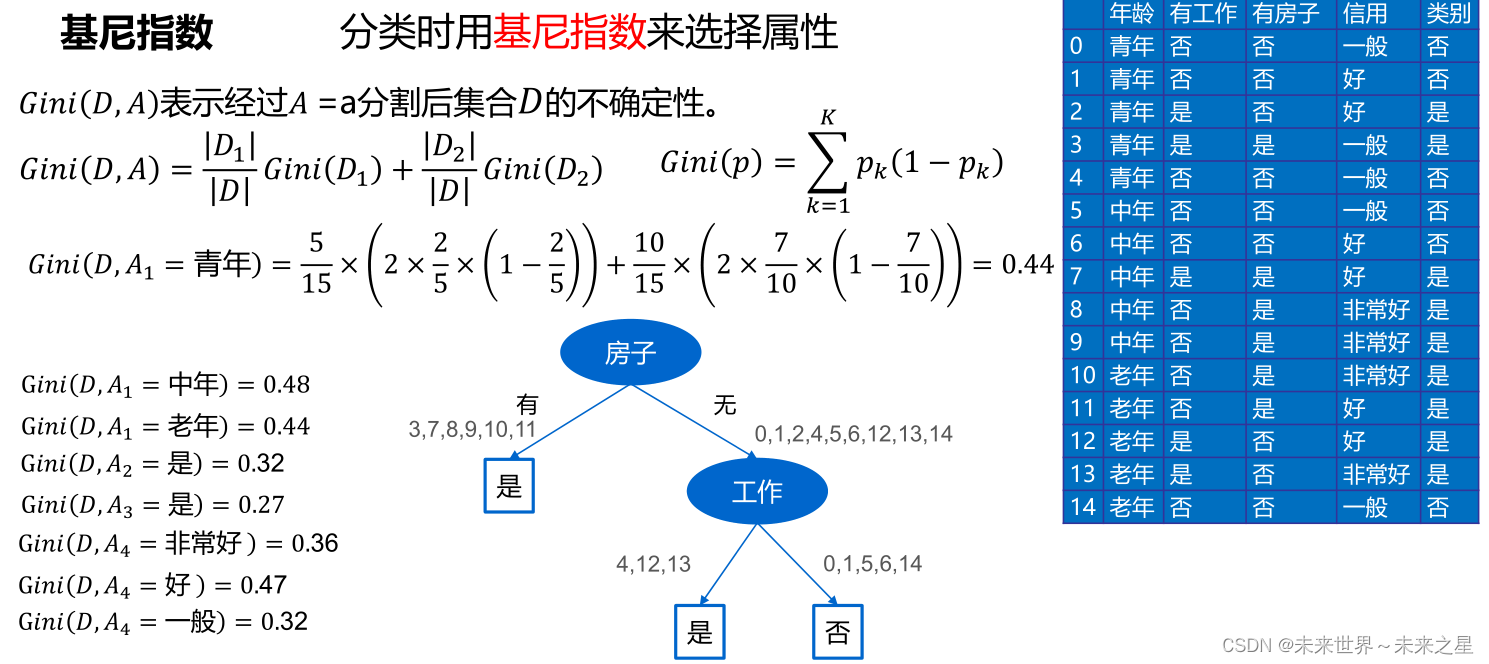
CART算法
- ⚫ClassificationandRegressionTree(CART)是决策树的一种。
- ⚫用基尼指数来选择属性(分类),或用均方差来选择属性(回归)。
- ⚫顾名思义,CART算法既可以用于创建分类树,也可以用于创建回归树,两者在构建的过程中稍有差异。
- ⚫如果目标变量是离散的,称为分类树。
- ⚫如果目标变量是连续的,称为回归树。
- CART算法-回归
- 用均方差来选择属性对于连续值的处理,
C
A
R
T
CART
CART分类树采用基尼系数的大小来度量特征的各个划分点。对于任意划分特征
A
A
A,对应的任意划分点
s
s
s两边划分成的数据集
D
1
D_{1}
D1和
D
2
D_{2}
D2,求出使
D
1
D_{1}
D1和
D
2
D_{2}
D2各自集合的均方差最小,同时
D
1
D_{1}
D1和
D
2
D_{2}
D2的均方差之和最小所对应的特征和特征值划分点。表达式为:
m i n a , s [ m i n c 1 ∑ x i ∈ D 1 ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ D 2 ( y i − c 2 ) 2 ] min_{a,s}[min_{c_{1}}\sum_{x_{i}\in D_{1}}{(y_{i}-c_{1})^{2}+min_{c_{2}}\sum_{x_{i}\in D_{2}}{(y_{i}-c_{2})}^{2}}] mina,s[minc1xi∈D1∑(yi−c1)2+minc2xi∈D2∑(yi−c2)2],其中, c 1 为 D 1 c_{1}为D_{1} c1为D1数据集合的样本输出均值, c 2 c_{2} c2为 D 2 D_{2} D2数据集样本输出的均值。
预测方式
- 对于决策树建立后做预测的方式,上面讲到了 C A R T CART CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果。
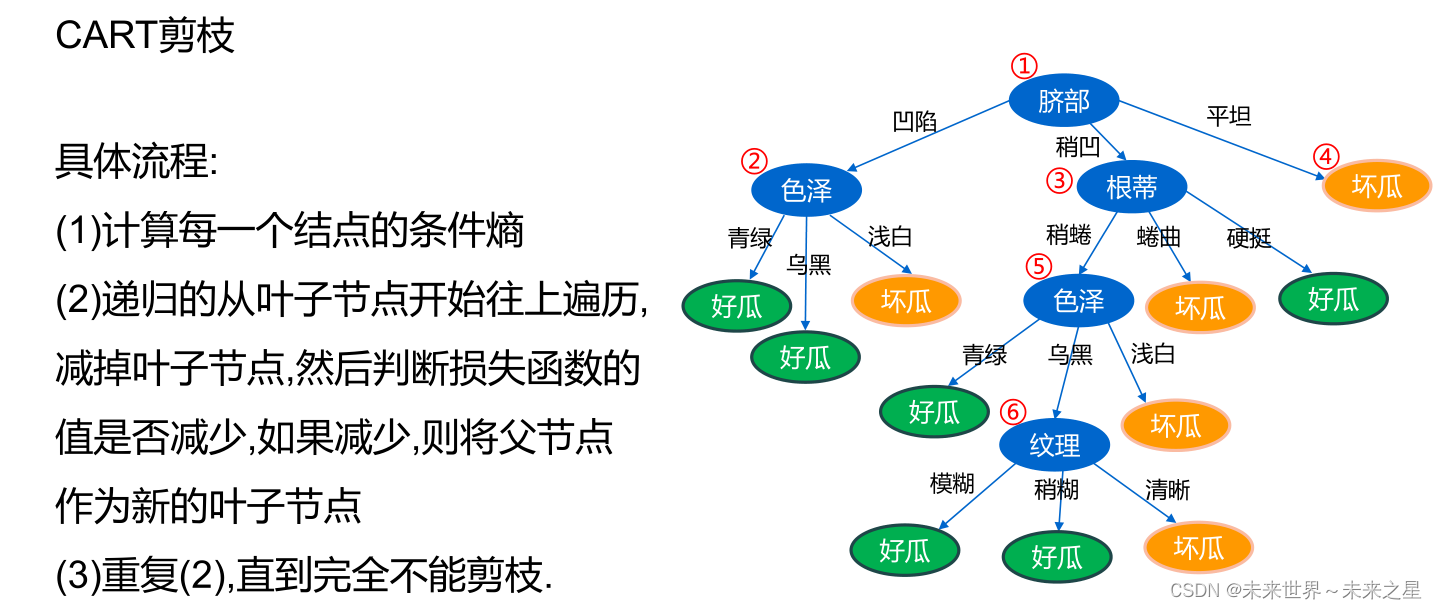
- CART算法采用一种“基于代价复杂度的剪枝”方法进行后剪枝,这种方法会生成一系列树,每个树都是通过将前面的树的某个或某些子树替换成一个叶节点而得到的,这一系列树中的最后一棵树仅含一个用来预测类别的叶节点。然后用一种成本复杂度的度量准则来判断哪棵子树应该被一个预测类别值的叶节点所代替。
- 这种方法需要使用一个单独的测试数据集来评估所有的树,根据它们在测试数据集熵的分类性能选出最佳的树。
决策树的差异
- 划分标准的差异:ID3 使用信息增益偏向特征值多的特征,C4.5 使用信息增益
率克服信息增益的缺点,偏向于特征值小的特征,CART 使用基尼指数克服
C4.5 需要求log 的巨大计算量,偏向于特征值较多的特征。 - 使用场景的差异:ID3 和C4.5 都只能用于分类问题,CART 可以用于分类和回
归问题;ID3 和C4.5 是多叉树,速度较慢,CART 是二叉树,计算速度很快; - 样本数据的差异:ID3 只能处理离散数据且缺失值敏感,C4.5 和CART 可以处
理连续性数据且有多种方式处理缺失值;从样本量考虑的话,小样本建议C4.5
、大样本建议CART。C4.5 处理过程中需对数据集进行多次扫描排序,处理成
本耗时较高,而CART 本身是一种大样本的统计方法,小样本处理下泛化误差
较大; - 样本特征的差异:ID3 和C4.5 层级之间只使用一次特征,CART 可多次重复使
用特征; - 剪枝策略的差异:ID3 没有剪枝策略,C4.5 是通过悲观剪枝策略来修正树的准
确性,而CART 是通过代价复杂度剪枝。
资料
代码
#%%
import numpy as np
import pandas as pd
import math
from math import log
#%%
# 创建数据
def create_data():
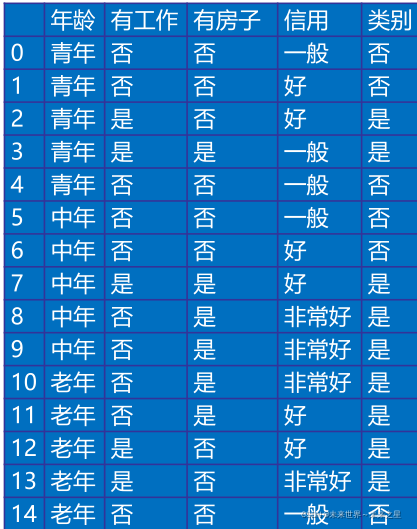
datasets=[['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
]
labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']
# 返回数据集和每个维度的名称
return datasets,labels
#%%
datasets,labels=create_data()
train_data = pd.DataFrame(datasets, columns=labels)
#%%
train_data
#%% md
# 计算熵
#%%
def calc_ent(datasets):
"""
datasets是数据集(包含标签label)
"""
data_length=len(datasets)
label_count={}
for i in range(data_length):
#获取label
label = datasets[i][-1]
#如果label不存在label_count中
if label not in label_count:
# 把label赋值为0
label_count[label]=0
# label标签统计加1
label_count[label]+=1
#计算信息熵
ent = -sum([(p/data_length)*log(p/data_length,2) for p in label_count.values()])
return ent
#%% md
# 条件熵
#%%
def cond_ent(datasets,axis=0):
data_length=len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p) / data_length) * calc_ent(p)
for p in feature_sets.values()])
return cond_ent
#%%
calc_ent(datasets)
#%% md
信息增益
#%%
def info_gain(ent, cond_ent):
return ent - cond_ent
#%%
def info_gain_train(datasets):
count = len(datasets[0]) - 1
ent = calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
print('特征({}) 的信息增益为: {:.3f}'.format(labels[c], c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return '特征({})的信息增益最大,选择为根节点特征'.format(labels[best_[0]])
#%%
info_gain_train(np.array(datasets))
#%% md
# 利用ID3算法生成决策树
#%%
# 定义节点类 二叉树
class Node:
def __init__(self, root=True, label=None, feature_name=None, feature=None):
self.root = root
self.label = label
self.feature_name = feature_name
self.feature = feature
self.tree = {}
self.result = {
'label:': self.label,
'feature': self.feature,
'tree': self.tree
}
def __repr__(self):
return '{}'.format(self.result)
def add_node(self, val, node):
self.tree[val] = node
def predict(self, features):
if self.root is True:
return self.label
return self.tree[features[self.feature]].predict(features)
class DTree:
def __init__(self, epsilon=0.1):
self.epsilon = epsilon
self._tree = {}
# 熵
@staticmethod
def calc_ent(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
ent = -sum([(p / data_length) * log(p / data_length, 2)
for p in label_count.values()])
return ent
# 经验条件熵
def cond_ent(self, datasets, axis=0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
for p in feature_sets.values()])
return cond_ent
# 信息增益
@staticmethod
def info_gain(ent, cond_ent):
return ent - cond_ent
def info_gain_train(self, datasets):
count = len(datasets[0]) - 1
ent = self.calc_ent(datasets)
best_feature = []
for c in range(count):
c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
best_feature.append((c, c_info_gain))
# 比较大小
best_ = max(best_feature, key=lambda x: x[-1])
return best_
def train(self, train_data):
"""
input:数据集D(DataFrame格式),特征集A,阈值eta
output:决策树T
"""
_, y_train, features = train_data.iloc[:, :
-1], train_data.iloc[:,
-1], train_data.columns[:
-1]
# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回T
if len(y_train.value_counts()) == 1:
return Node(root=True, label=y_train.iloc[0])
# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回T
if len(features) == 0:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])
# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
max_feature_name = features[max_feature]
# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回T
if max_info_gain < self.epsilon:
return Node(
root=True,
label=y_train.value_counts().sort_values(
ascending=False).index[0])
# 5,构建Ag子集
node_tree = Node(
root=False, feature_name=max_feature_name, feature=max_feature)
feature_list = train_data[max_feature_name].value_counts().index
for f in feature_list:
sub_train_df = train_data.loc[train_data[max_feature_name] ==
f].drop([max_feature_name], axis=1)
# 6, 递归生成树
sub_tree = self.train(sub_train_df)
node_tree.add_node(f, sub_tree)
# pprint.pprint(node_tree.tree)
return node_tree
def fit(self, train_data):
self._tree = self.train(train_data)
return self._tree
def predict(self, X_test):
return self._tree.predict(X_test)
#%%
datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
#%%
tree
#%%
dt.predict(['老年', '否', '否', '一般'])
#%% md
# Scikit-learn实例
#%%
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
#%% md
使用Iris数据集,我们可以构建如下树:
#%%
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
data = np.array(df.iloc[:100, [0, 1, -1]])
# print(data)
return data[:, :2], data[:, -1],iris.feature_names[0:2]
X, y,feature_name= create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
#%% md
# 决策树分类
#%%
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz
from sklearn import tree
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)
clf.score(X_test, y_test)
#%% md
# 一旦经过训练,就可以用 plot_tree函数绘制树
#%%
tree.plot_tree(clf)
#%% md
# 也可以导出树
#%%
tree_pic = export_graphviz(clf, out_file="mytree.pdf")
with open('mytree.pdf') as f:
dot_graph = f.read()
#%%
graphviz.Source(dot_graph)
#%% md
或者,还可以使用函数 export_text以文本格式导出树。此方法不需要安装外部库,而且更紧凑:
#%%
from sklearn.tree import export_text
r = export_text(clf,feature_name)
print(r)
#%% md
# 决策树回归
#%%
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
#%%
# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))
#%%
# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)
# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue", label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
#%% md
# Scikit-learn 的决策树参数
# 决策树调参
#%%
# 导入库
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor
from sklearn import metrics
#%%
# 导入数据集
X = datasets.load_iris() # 以全部字典形式返回,有data,target,target_names三个键
data = X.data
target = X.target
name = X.target_names
x, y = datasets.load_iris(return_X_y=True) # 能一次性取前2个
print(x.shape, y.shape)
#%%
# 数据分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x,
y,
test_size=0.2,
random_state=100)
#%%
# 用GridSearchCV寻找最优参数(字典)
param = {
'criterion': ['gini'],
'max_depth': [30, 50, 60, 100],
'min_samples_leaf': [2, 3, 5, 10],
'min_impurity_decrease': [0.1, 0.2, 0.5]
}
grid = GridSearchCV(DecisionTreeClassifier(), param_grid=param, cv=6)
grid.fit(x_train, y_train)
print('最优分类器:', grid.best_params_, '最优分数:', grid.best_score_) # 得到最优的参数和分值
#%%