基于A*的网格地图最短路径问题求解
一、A*算法介绍、原理及步骤
A*算法是一种启发式算法,比起Dijkstra算法的盲目搜索,A*算法的搜索路径更具有目的性,其性能取决于所给的启发式信息,即启发函数的准确度,启发函数的准确度越接近于实际距离,则算法效率越高,结果越精确,然而它并不能保证能够得到最优解,对比于图论中的算法,它更适用于节点数量巨大的情形,因此常用于游戏、机器人或无人驾驶的自动寻路与路径规划问题中。
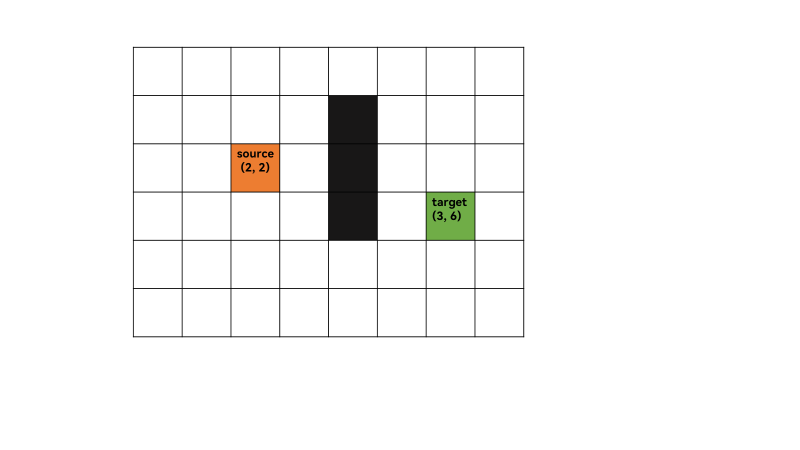
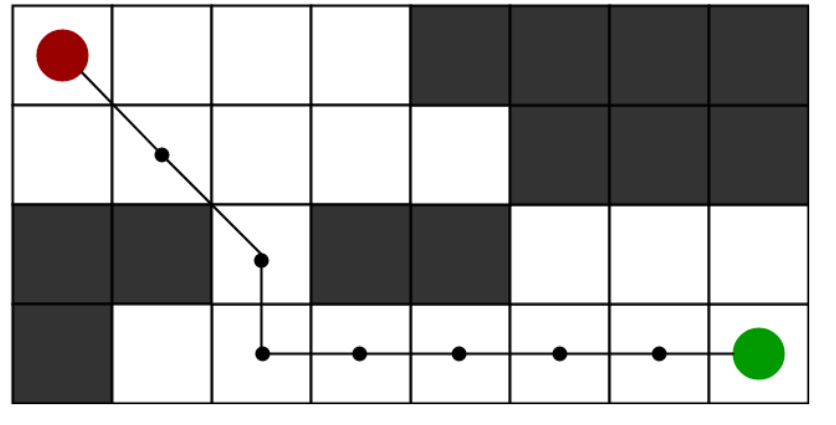
许多游戏和基于web的地图都使用这种算法来非常有效地找到最短路径(近似)。为了在现实生活中接近最短路径,比如在地图中,有很多障碍的游戏中。我们可以考虑一个有几个障碍的二维网格,我们从一个起点(下图红色)开始,寻找到达终点(下图绿色)的最短路径问题。
A*算法思想:
A*搜索算法所做的是,从起点开始,根据一个值
f
f
f选择下一步移动的网格,
f
=
g
+
h
f=g+h
f=g+h。在每一步中,它选择具有最低
f
f
f的节点进行处理。
其中:
- g g g为从起始点移动到给定方格的移动成本
- h h h为从给定方格移动到最终目的地的估计移动成本,通常被称为启发式函数,是一种猜测或者估算。在找到路径之前,不可能知道实际的距离,因为各种各样的东西都可能挡在路上(墙壁、水等)。计算 h h h的方法有很多。
算法步骤如下:
输入:图,起点
src
\text{src}
src,终点
tgt
\text{tgt}
tgt, 每个点的父节点
node_parent
\text{node\_parent}
node_parent用于保存最有路径。
输出:起点到终点的最短路径。
step1.
\text{step1.}
step1. 初始化open list和closed list,将起点加入open list,并设置优先级为0(优先级最高)。【注】open list可以是一个优先队列。
step2.
\text{step2.}
step2.
while open list is not empty:
\text {while open list is not empty}:
while open list is not empty:
a)查找open list中
f
f
f值最小的节点,把它作为当前要处理的节点cur_node,将cur_node从open list中删除。
b)
if cur_node == tgt
\text {if cur\_node == tgt}
if cur_node == tgt,跳出
while
\text {while}
while循环,停止搜索
c)
else:
\text {else:}
else:
i)获取
cur_node
\text{cur\_node}
cur_node的相邻8个方格
successors
\text{successors}
successors
ii)将
cur_node
\text{cur\_node}
cur_node加入
close list
\text{close list}
close list
iii)遍历
successors
\text{successors}
successors,对于每个
successor
\text{successor}
successor:
1)若
successor
\text{successor}
successor在close list中,跳过本次循环(continue)
2)若
successor
\text{successor}
successor不在open list中,计算
successor
\text{successor}
successor的g、h和f值。
①
succesor.g=cur_node.g+cur_node
\text{succesor.g=cur\_node.g+cur\_node}
succesor.g=cur_node.g+cur_node到
successor
\text{successor}
successor的欧几里得距离;
②
succesor.h
\text{succesor.h}
succesor.h=从
successor
\text{successor}
successor到终点的曼哈顿距离。
③
succesor.f=succesor.g+succesor.h。
\text{succesor.f=succesor.g+succesor.h。}
succesor.f=succesor.g+succesor.h。
④ 将
succesor
\text{succesor}
succesor加入
open list
\text{open list}
open list。
3)若
successor
\text{successor}
successor在open list中,判断从
cur_node
\text{cur\_node}
cur_node到successor的距离是否>succesor.g,若是则
①
succersor.g=cur_node.g;
\text{succersor.g=cur\_node.g;}
succersor.g=cur_node.g;
②
succesor.f=succesor.g + succesor.h;
\text{succesor.f=succesor.g + succesor.h;}
succesor.f=succesor.g + succesor.h;
③
node_parent[neighbor] = node
\text{node\_parent[neighbor] = node}
node_parent[neighbor] = node
二、Dijkstra算法和A*的区别
- Dijkstra算法计算源点到其他所有点的最短路径长度,A*关注点到点的最短路径(包括具体路径)。
- A*可以轻松地用在比如无人机航路规划、游戏地图寻路中(grid),而Dijkstra建立在较为抽象的图论层面(graph)。
- Dijkstra算法的实质是广度优先搜索,是一种发散式的搜索,所以空间复杂度和时间复杂度都比较高。对路径上的当前点,A*算法不但记录其到源点的代价,还计算当前点到目标点的期望代价,是一种启发式算法,也可以认为是一种深度优先的算法。
- 由第一点,当目标点很多时,A*算法会带入大量重复数据和复杂的估价函数,所以如果不要求获得具体路径而只比较路径长度时,Dijkstra算法会成为更好的选择。
三、A*算法应用场景
What if the search space is not a grid and is a graph ?
The same rules applies there also. The example of grid is taken for the simplicity of understanding. So we can find the shortest path between the source node and the target node in a graph using this A* Search Algorithm, just like we did for a 2D Grid.
应该使用哪种算法在图上查找路径?
1.如果要查找从所有位置起始或到所有位置的路径,使用广度优先搜索或Dijkstra算法。如果移动成本相同,使用广度优先搜索;如果移动成本不同,使用Dijkstra算法。
2.如果想找到通往一个位置或几个目标中最接近的位置的路径,使用Greedy Best First Search或A*。大多数情况下选择A*。当使用贪婪最佳优先搜索时,可以考虑使用带有“不可接受”启发式的A*。
图形搜索算法可以用于任何类型的图。图上的移动成本变成在图边上的权重。启发式距离不容易转化到不同的图中,必须为每种类型的图设计一个启发式距离。
四、启发函数
上面已经提到,启发函数h(n)会影响A算法的行为。在极端情况下,当启发函数h(n)始终为0,则将由g(n)决定节点的优先级,此时算法就退化成了Dijkstra算法。如果h(n)始终小于等于节点n到终点的代价,则A算法保证一定能够找到最短路径。但是当h(n)的值越小,算法将遍历越多的节点,也就导致算法越慢。如果h(n)完全等于节点n到终点的代价,则A算法将找到最佳路径,并且速度很快。可惜的是,并非所有场景下都能做到这一点。因为在没有达到终点之前,我们很难确切算出距离终点还有多远。
如果h(n)的值比节点n到终点的代价要大,则A算法不能保证找到最短路径,不过此时会很快。
在另外一个极端情况下,如果h()n相较于g(n)大很多,则此时只有h(n)产生效果,这也就变成了最佳优先搜索。
由上面这些信息我们可以知道,通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况,我们可能未必需要最短路径,而是希望能够尽快找到一个路径即可。这也是A*算法比较灵活的地方。
对于网格形式的图,有以下这些启发函数可以使用:
如果图形中只允许朝上下左右四个方向移动,则可以使用曼哈顿距离(Manhattan distance)。
如果图形中允许朝八个方向移动,则可以使用对角距离。
如果图形中允许朝任何方向移动,则可以使用欧几里得距离(Euclidean distance)。
五、距离
- 如果图形中只允许朝上下左右四个方向移动,则启发函数可以使用曼哈顿距离;
- 如果图形中允许斜着朝邻近的节点移动,则启发函数可以使用对角距离。
六、基于A*的网格地图最短路径问题求解
实例分析
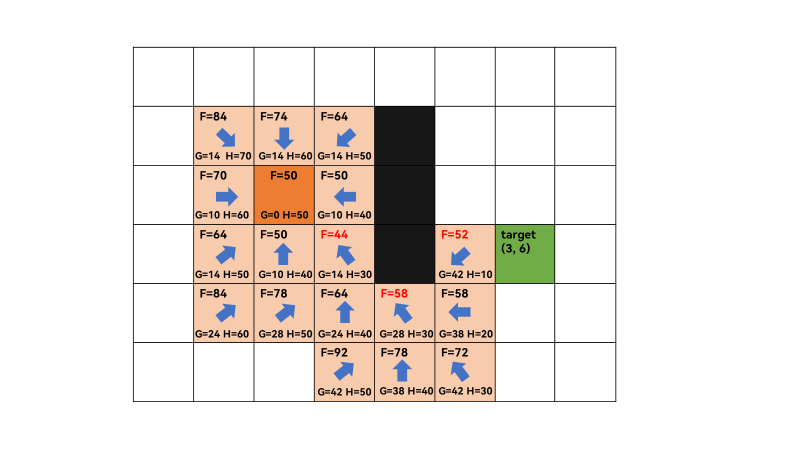
1、计算grid中从从起点(2,2)到终点(3,6)的最短路。初始化open list,close list,将起点(2,2)加入到open list中,其优先级为0(最高),这里可以看出open list可以用优先队列。
2、open list不为空,遍历 open list ,查找F值最小的节点q,此时q为起点,获取对当前方格q的 8 个相邻方格(successors),[(1, 1), (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2), (3, 3)],遍历successors,对于每一个successor,计算G ,H,和F值,F=G+H,G通过欧几里得距离计算,如(2,2)和(1,1)之间的G值为
(
2
−
1
)
2
+
(
2
−
1
)
2
=
2
=
1.4
\sqrt{(2-1)^2+(2-1)^2}=\sqrt 2 = 1.4
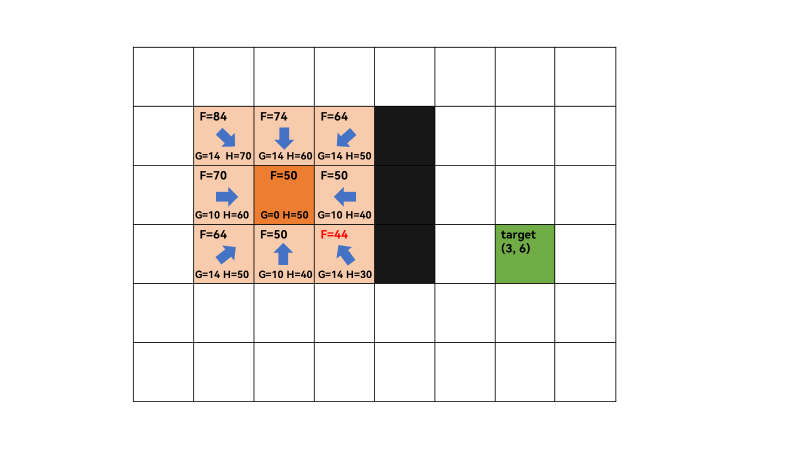
(2−1)2+(2−1)2=2=1.4,计算机中浮点数运算会产生容差(tolerance),这里记为14。H值为当前successor到终点的曼哈顿距离,是一个估计距离,因为还没找到最短路,不可能直接计算出确切值。如(1,1)和(3,6)之间的H值为70,故(1,1)的F值=G+H=84。同理可计算起点的其它successors的F值。最后将8个相邻方格加入open list,第一次迭代结束,将q加入close list。
点(x1,y1)和(x2,y2)间的欧几里得距离为 ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} (x1−x2)2+(y1−y2)2
点(x1,y1)和(x2,y2)间的曼哈顿距离为 ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ |x_1-x_2|+|y_1-y_2| ∣x1−x2∣+∣y1−y2∣
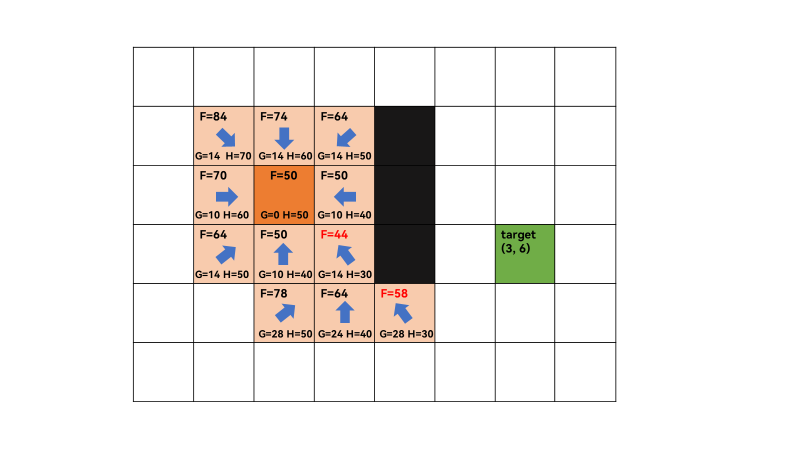
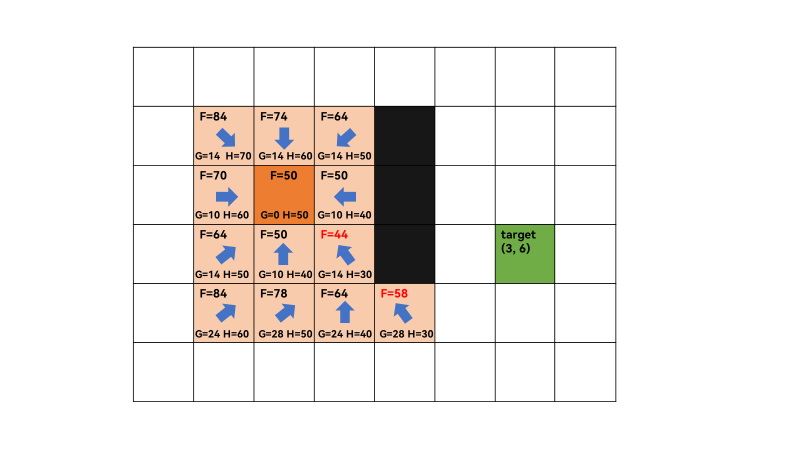
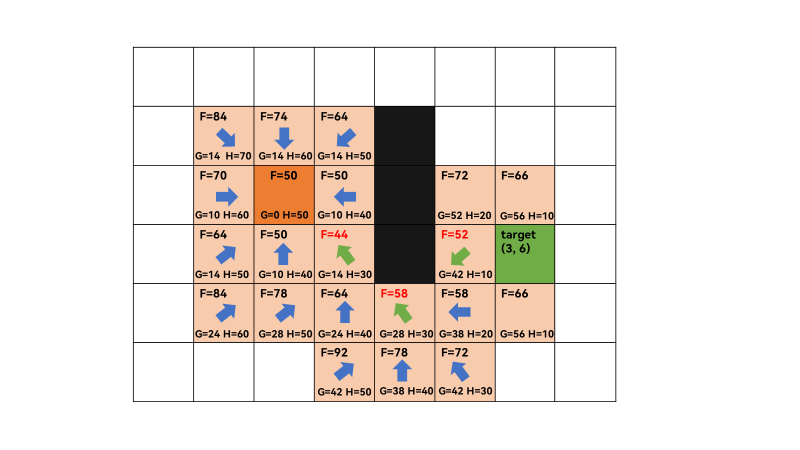
3、重复上一步,open list不为空,遍历 open list ,查找F值最小的节点q,此时q为(3,3),F=44最小,获取q=(3,3)的相邻方格,successors=[(2, 2), (2, 3), (3, 2), (4, 2), (4, 3), (4, 4)],由于(2,4)和(3,4)为障碍,所以不算相邻方格。此时,(2,2)和(3,3)在close list中,遍历相邻方格F值,需要跳过。
完整代码
将实例分析中的网格地图映射为二维矩阵,其中1表示该网格可以通过,0表示为障碍。src=(2,2),tgt=(3,6)
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1],`
创建一个节点类Node,表示网格地图中的每一个网格(节点),Node类有4个属性值,分别是坐标、f值、g值、h值。将Node节点加入open list(优先队列)中,每次按优先级(f越小优先级越高)进行出队。重写equals方法和哈希方法,用坐标唯一标志一个Node。重写__lt__()方法使Node按f值比较大小。
完整代码如下:
from collections import defaultdict
from typing import Tuple
from queue import PriorityQueue
import numpy as np
import pandas as pd
import logging
logging.basicConfig(level=logging.DEBUG, format='%(message)s')
# 显示所有列
pd.set_option('display.max_columns', None)
# 显示所有行
pd.set_option('display.max_rows', None)
# 不换行打印
pd.set_option('display.width', 5000)
class Node:
def __init__(self, coord, priority=0):
self.coord = coord
self.f = priority
self.g = 0
self.h = 0
def __eq__(self, other):
return self.coord == other.coord
def __hash__(self):
return hash(self.coord)
def __lt__(self, other):
return self.f < other.f
def __getitem__(self, item):
return self.coord
def __repr__(self):
return str({'坐标': self.coord, 'f': self.f})
class Grid:
def __init__(self, ):
# self.grid = np.asarray([
# [1, 0, 1, 1, 1, 1, 0, 1, 1, 1],
# [1, 1, 1, 0, 1, 1, 1, 0, 1, 1],
# [1, 1, 1, 0, 1, 1, 0, 1, 0, 1],
# [0, 0, 1, 0, 1, 0, 0, 0, 0, 1],
# [1, 1, 1, 0, 1, 1, 1, 0, 1, 0],
# [1, 0, 1, 1, 1, 1, 0, 1, 0, 0],
# [1, 0, 0, 0, 0, 1, 0, 0, 0, 1],
# [1, 0, 1, 1, 1, 1, 0, 1, 1, 1],
# [1, 1, 1, 0, 0, 0, 1, 0, 0, 1]]
# )
# // Driver program to test above function
# /* Description of the Grid-
# 1--> The cell is not blocked
# 0--> The cell is blocked */
self.grid = np.asarray([
[1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
])
self.nodes = []
logging.info(self.grid)
for x in range(self.grid.shape[0]):
for y in range(self.grid.shape[1]):
coord = (x, y)
node = Node(coord)
self.nodes.append(node)
def is_valid(self, node):
x, y = node
if x < 0 or x > self.grid.shape[0] - 1 or y < 0 or y > self.grid.shape[1] - 1:
return False
if self.grid[x][y] == 0:
return False
return True
def get_neighbors(self, node: Node):
x, y = node.coord
neighbors = [(x - 1, y - 1), (x - 1, y), (x - 1, y + 1),
(x, y - 1), (x, y + 1),
(x + 1, y - 1), (x + 1, y), (x + 1, y + 1)]
valid_neighbors = [neighbor for neighbor in neighbors if self.is_valid(neighbor)]
valid_neighbors = [Node(neighbor) for neighbor in valid_neighbors]
return valid_neighbors
def manhattan_distance(self, node_i, node_j):
x1, y1 = node_i.coord
x2, y2 = node_j.coord
return np.abs(x1 - x2) + np.abs(y1 - y2)
def euclidean_distance(self, node_i, node_j):
x1, y1 = node_i.coord
x2, y2 = node_j.coord
return np.sqrt(np.power((x1 - x2), 2) + np.power((y1 - y2), 2))
def a_star_algorithm(grid, src, tgt):
src = Node(src)
tgt = Node(tgt)
shortest_path = [tgt]
open_list = PriorityQueue()
closed_list = set()
open_list.put(src)
node_parent = {}
while not open_list.empty():
node = open_list.get()
if node == tgt: # 若为终点,
cur = node_parent[tgt]
while cur != src:
shortest_path.append(cur)
cur = node_parent[cur]
shortest_path.append(src)
shortest_path.reverse()
break
else: # 不是终点,
neighbors = grid.get_neighbors(node)
closed_list.add(node)
for neighbor in neighbors:
if neighbor in closed_list:
continue
if neighbor not in open_list.queue:
node_parent[neighbor] = node # 将当前邻接点neighbor的父节点为node,k=父节点,v=子节点
neighbor.g = node.g + grid.euclidean_distance(node, neighbor)
neighbor.h = grid.manhattan_distance(neighbor, tgt)
neighbor.f = neighbor.g + neighbor.h
open_list.put(neighbor)
if neighbor in open_list.queue:
if node.g + grid.euclidean_distance(node, neighbor) > neighbor.g:
neighbor.g = node.g
neighbor.f = neighbor.g + neighbor.h
node_parent[neighbor] = node
# 打印地图每个点的f值
df = pd.DataFrame(index=np.arange(0, 6), columns=np.arange(0, 8), dtype=np.float_)
for node in node_parent.keys():
x, y = node.coord
df.loc[x, y] = node.f
print(df)
return shortest_path
if __name__ == "__main__":
grid = Grid()
shortest_path = a_star_algorithm(grid, (2, 2), (3, 6))
logging.info(f'最优路径:{shortest_path}')
程序运行结果如下:
[[1 1 1 1 1 1 1 1]
[1 1 1 1 0 1 1 1]
[1 1 1 1 0 1 1 1]
[1 1 1 1 0 1 1 1]
[1 1 1 1 1 1 1 1]
[1 1 1 1 1 1 1 1]]
最优路径:[{'坐标': (2, 2), 'f': 0}, {'坐标': (3, 3), 'f': 4.414213562373095}, {'坐标': (4, 4), 'f': 5.82842712474619}, {'坐标': (3, 5), 'f': 5.242640687119286}, {'坐标': (3, 6), 'f': 0}]
0 1 2 3 4 5 6 7
0 NaN NaN NaN NaN NaN NaN NaN NaN
1 NaN 8.414214 7.000000 6.414214 NaN NaN NaN NaN
2 NaN 7.000000 NaN 5.000000 NaN 7.242641 6.656854 NaN
3 NaN 6.414214 5.000000 4.414214 NaN 5.242641 5.242641 NaN
4 NaN 8.414214 7.828427 6.414214 5.828427 5.828427 6.656854 NaN
5 NaN NaN NaN 9.242641 7.828427 7.242641 NaN NaN
Process finished with exit code 0
七、A*算法的改进思路
【路径规划】A*算法方法改进思路简析
参考:
-
https://www.geeksforgeeks.org/a-search-algorithm/