Multi-view Classification Using Hybrid Fusion and Mutual Distillation

Intro

多视角问题可以分为两类：

1. Structured。固定视角，或预先定义的视角的问题。
2. unstructured。

本文的三大contributions：

1. 引入了混合的多视角融合策略。
2. 使用了互蒸馏策略。具体而言，对多视角融合预测，与单视角预测均值，采用distillation loss。
3. 证实了在多种多视角任务当中的有效性。

Related Work

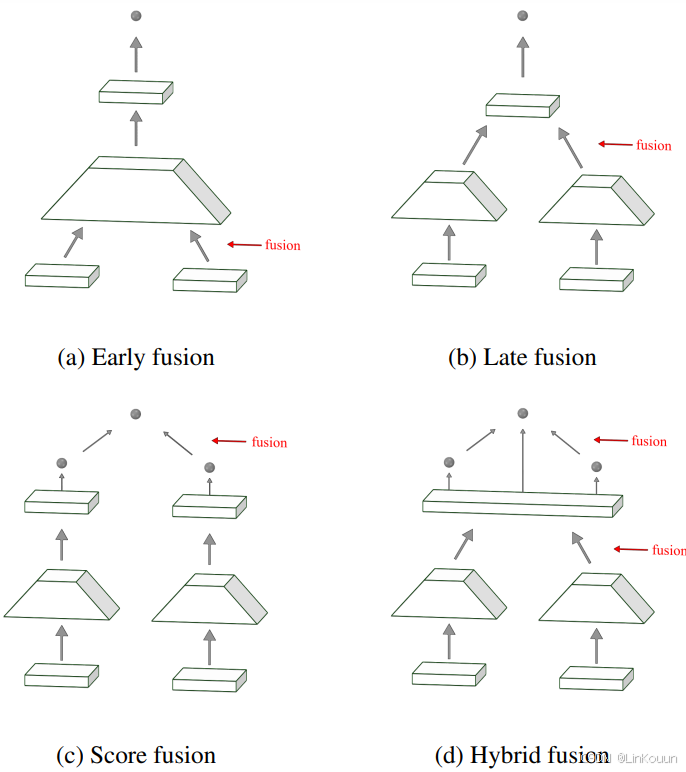
Fusion策略分类。

1. Early Fusion：在low-level对feature进行融合，之后的训练过程与单视角情况一致。
   缺点：low-level feature没经过网络的深层次处理，过早的融合特征可能会将一些task-irrelevant features融入进去。
2. Late Fusion：先利用某些网络（如CNN）独立从input中学习feature，然后对特征进行融合。
   比如：简单的串接feature，然后再对融合后的特征做池化。
3. Score Fusion：极端的late fusion。每个单视角分别预测，然后只融合最后的预测vector（预测分数）。

• 本文采用 Hybrid 策略：结合了score fusion和score fusion。
• 本文引入了多视角预测与score-fused的单视角预测（具体而言是，求所有单个视角预测分数的均值）的互蒸馏。

Method

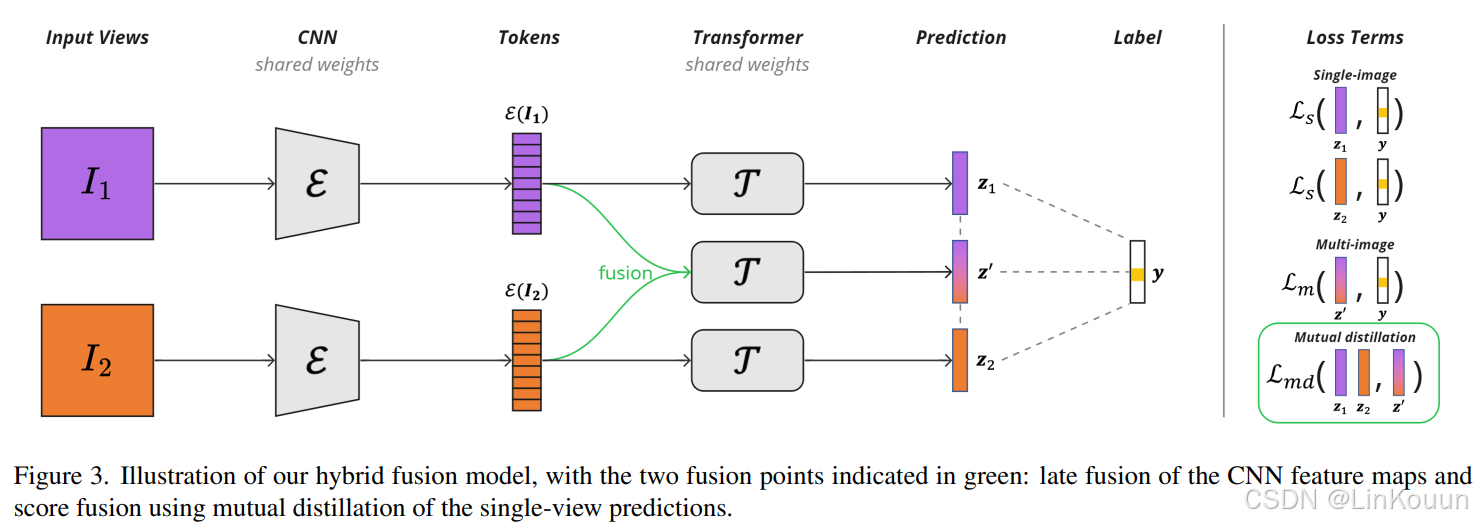
整体Pipeline如下：

算法流程：

1. $I_1$为第一个视角的输入样本。每个视角的输入分别送入CNN中，得到feature：

   • $\mathcal{C}(I)\in {\mathbb{R}}^{h\times w\times c}$：CNN输出特征。维度分别为高，宽，通道数。

2. 将$\mathcal{C}(I)$转为Token形式，以便之后送入Transformer：首先将空间维度$(h,w)$拉成一维$S=hw$；然后将其encode成token形式：
   $$\begin{array}{c}\mathcal{E}\left(\mathbf{I}\right)=\mathcal{C}\left(\mathbf{I}\right)\mathbf{E}+{\mathbf{E}}_{\mathbf{pos}}\end{array}$$

   • $\mathbf{E}\in {\mathbb{R}}^{c\times d}$：投影矩阵。
   • ${\mathbf{E}}_{\text{pos}}$：可学习的positional encoding。
   • 最后将Eq1结果串接一个$x_{\text{class}}\in {\mathbb{R}}^{1\times d}$
     $\mathcal{E}\left(\mathbf{I}\right)\in {\mathbb{R}}^{S\times d}$，相当于长度为S的序列，每个token维度为d。

3. 将$\mathcal{E}\left(\mathbf{I}\right)$送入Transformer中。其中单个视角分别送入各自的Transformer，输出单一视角预测；多个视角特征融合，送入一个Transformer，输出多视角预测。N个视角的输入图像，对应N+1个Transformer。

   • 单视角预测：
     $$\begin{array}{c}z=\mathcal{T}\left(\left[x_{\mathbf{class}};\mathcal{E}\left(\mathbf{I}\right)\right]\right)\end{array}$$
     $\mathcal{T}$表示Transformer

   • 多视角预测：
     $$\begin{array}{c}{\mathbf{z}}^{\prime }=\mathcal{T}\left(\left[{\mathbf{x}}_{\mathbf{class}};{\mathcal{E}}^{\prime }\left({\mathbf{I}}_1\right);{\mathcal{E}}^{\prime }\left({\mathbf{I}}_2\right);...;{\mathcal{E}}^{\prime }\left({\mathbf{I}}_N\right)\right]\right)\end{array}$$
     其中$\mathbf{z},{\mathbf{z}}^{\prime }\in {\mathbb{R}}^{1\times k}$为prediction vector。$k$为分类个数。

4. 使用联合损失函数：
   $$\begin{array}{c}\mathcal{L}={\mathcal{L}}_m+{\mathcal{L}}_s+\lambda {\mathcal{L}}_{md}\end{array}$$
   分为三大部分：

   1. ${\mathcal{L}}_m$：多视角预测损失。为多视角融合特征的预测结果，与ground-truth label的损失。
   2. ${\mathcal{L}}_s$：单视角平均预测损失：所有单视角预测损失的平均值（score-fused）。
   3. ${\mathcal{L}}_{md}$：互蒸馏损失。

   L m d ( { z 1 , . . . , z N } , z ′ ; τ ) = 1 2 τ 2 ( L k d ( z ˉ ^ , z ′ ; τ ) + L k d ( z ^ ′ , z ˉ ; τ ) ) \begin{align} & \mathcal{L}_{md}\left(\{\boldsymbol{z}_1,...,\boldsymbol{z}_N\},\boldsymbol{z}^{\prime};\tau\right) \notag \\ = & \frac{1}{2}\tau^2 \left(\mathcal{L}_{kd}\left(\hat{\bar{\boldsymbol{z}}},\boldsymbol{z^{\prime}};\tau\right)+\mathcal{L}_{kd}\left(\hat{\boldsymbol{z}}^{\prime},\bar{\boldsymbol{z}};\tau\right)\right) \end{align} =​Lmd​({z1​,...,zN​},z′;τ)21​τ2(Lkd​(zˉ^,z′;τ)+Lkd​(z^′,zˉ;τ))​​

   • $\bold{\hat{}} \quad $：表示不进行反向传播的tensor（gradient-detached copy）。
   • $\bar{\mathbf{z}}=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{z}}_i$。N表示N个视角。

• $\bar{\mathbf{z}}=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{z}}_i$。N表示N个视角。