文章目录
一、矩阵乘法回顾
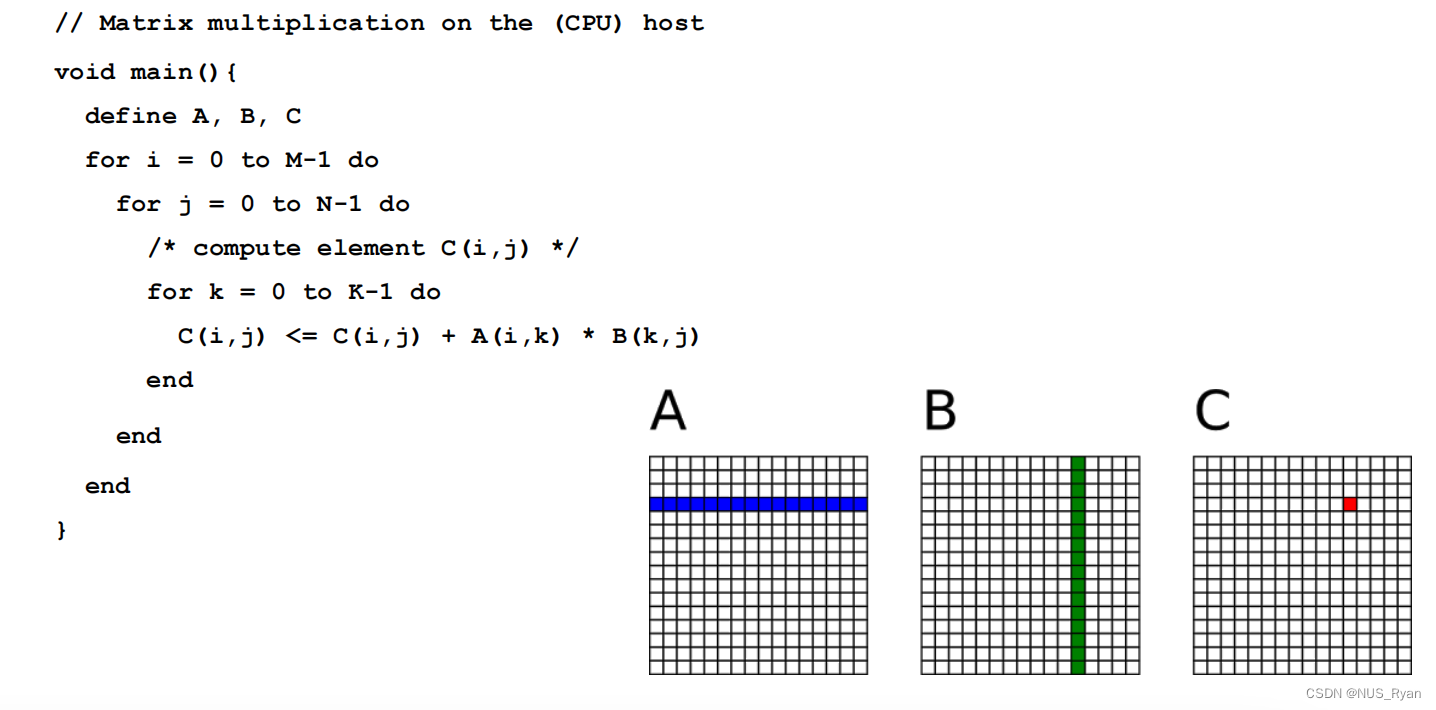
CPU版本:
GPU版本:
核函数如下:
C = AB ([mk],[kn])的矩阵乘法运算,每个线程都要读取A的一整行和B的一整列。A矩
阵中的每个点需要被读N次,B矩阵中的每个点需要被读M次。
因此我们可以将多次访问的数据放到共享内存中,减少重复读取的次数,并充分利用共享内存
的延迟低的优势。
二、CUDA内存架构
对于不同的寄存器和硬件,线程读写速度对比如下:
- 各自线程寄存器(~1周期)
- 线程块共享内存(~5周期)
- Grid全局内存(~500周期)
- Grid常量内存(~5周期)
因此,我们可以把频繁IO的变量放在线程块共享内存。
CUDA中的共享内存
CUDA中的共享内存是一种特殊类型的内存,其内容在源代码中被显式声明和使用
• 位于处理器中
• 以更高的速度访问(延迟&吞吐) • 仍然被内存访问指令访问
• 在计算机体系结构中通常称为暂存存储器
共享内存有以下特点:
• 读取速度等同于缓存,在很多显卡上,缓存和共享内存使用的是同一块硬
件,并且可以配置大小
• 共享内存属于线程块,可以被一个线程块内的所有线程访问
• 共享内存的两种申请空间方式,静态申请和动态申请
• 共享内存的大小只有几十K,过度使用共享内存会降低程序的并行性
CUDA中的共享内存使用方法
1.申请
• __shared__关键字 • 静态申请
• 动态申请
2.使用
• 将每个线程从全局索引位置读取元素,将它存储到共享内存之中。
• 注意数据存在着交叉,应该将边界上的数据拷贝进来。
• 块内线程同步: __syncthreads()。
注意,在使用__syncthreads()同步线程的时候,请避免使用如下同步的方法:
__share__ val[];
if(index < n){
if(tid condition){
do something with val; __syncthreads();
} else{
do something with val; __syncthreads();
}
}
该种写法会造成线程发散,举个例子,假设我们有一个简单的线程块,包含4个线程,要求偶数线程和奇数线程分别执行不同的操作:
__global__
void exampleKernel(float* data) {
int tid = threadIdx.x;
int index = threadIdx.x + blockDim.x * blockIdx.x;
__shared__ float val[4];
if (index < 4) {
if (tid % 2 == 0) {
val[tid] = data[tid] * 2;
} else {
val[tid] = data[tid] * 3;
}
__syncthreads();
// Do some other operations here after synchronization
}
}
静态申请内存
__global__ void staticReverse(int *d,int n){
__shared__ int s[64]; //内存大小固定
int t = threadIdx.x;
int tr = n - t - 1;
s[t] = d[t];
__syncthreads();
d[t] = s[tr]; //这一步没有对共享内存进行操作,所以不需要sync
}
staticReverse<<<1,n>>>(d_d,n);
动态申请内存
__global__ void dynamicReverse(int *d,int n){
extern __shared__ int s[];
int t= threadIdx.x;
int tr = n - 1- t;
s[t] = d[t];
__syncthreads();
d[t] = s[tr];
}
dynamicReverse<<<1,n,n * sizeof(int)>>> (d_d,n); //核函数被调用的时候需要传入动态内存的大小
三、分解矩阵乘法 / 平铺矩阵乘法
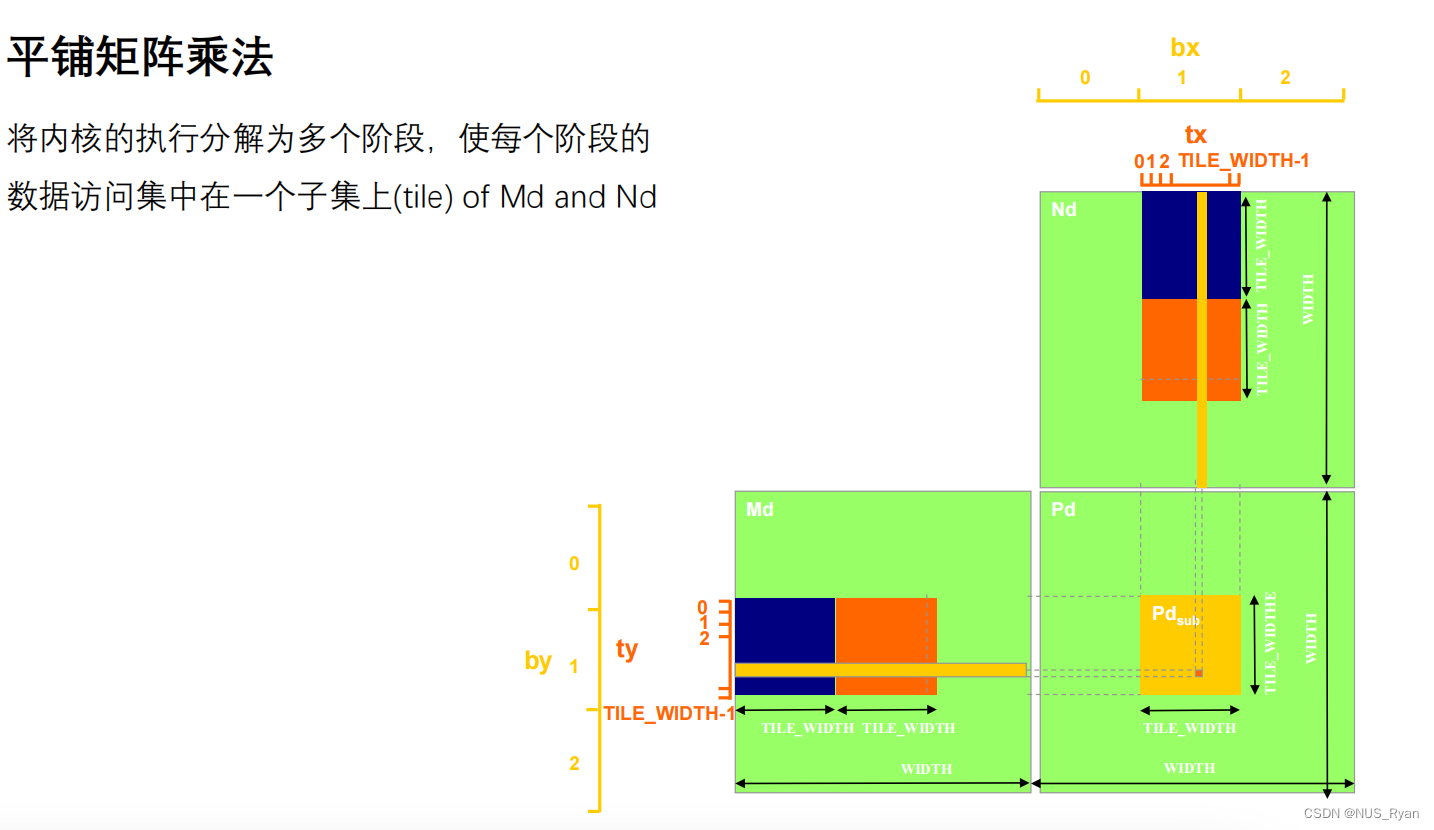
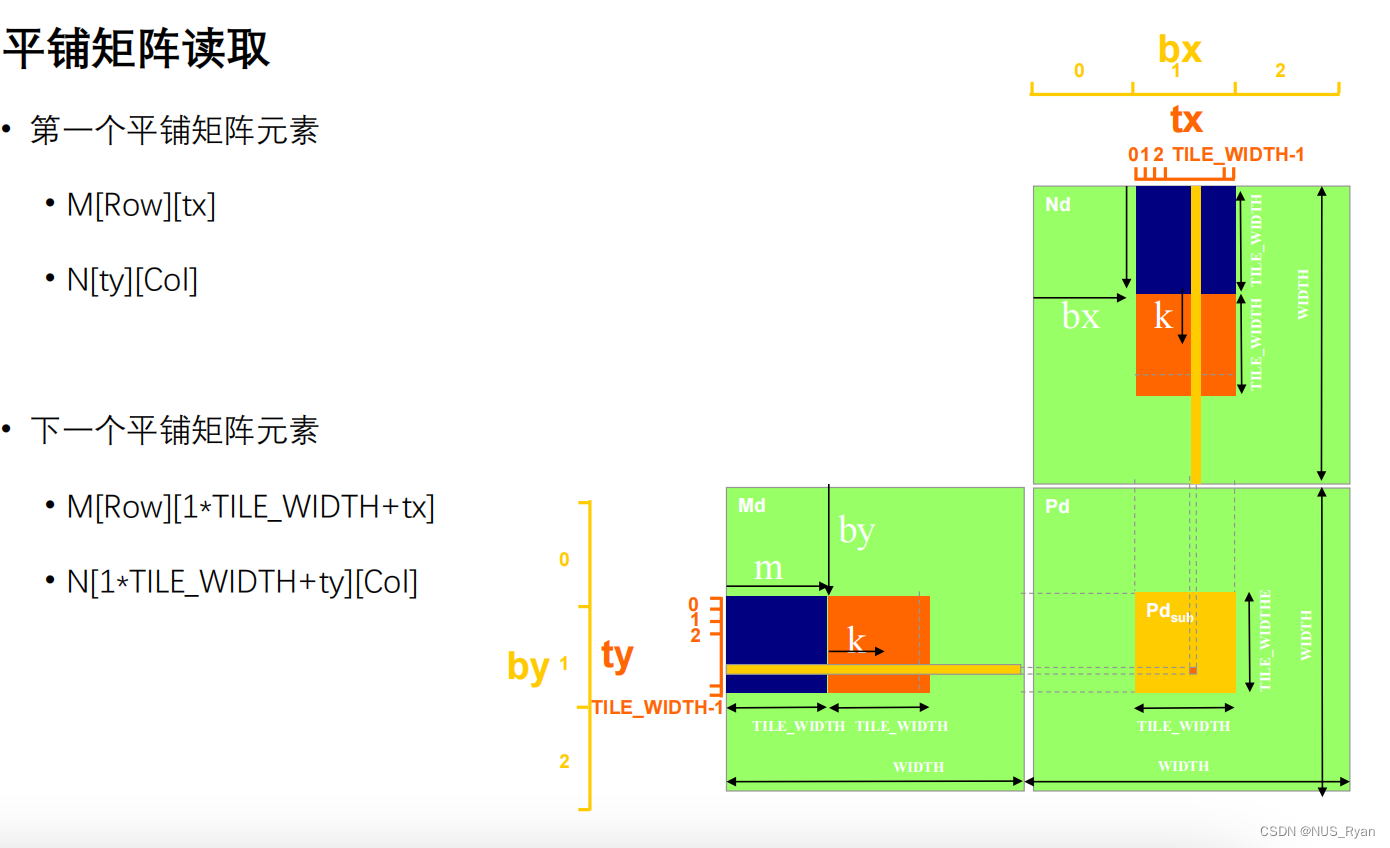
为了高效利用共享内存,我们使用一种叫做分解矩阵乘法的算法:
对于平铺矩阵算法,对于每一个Block,首先将其存储在共享内存中, 花费 * Block_Size ^ 2,对BLock_SIze中每一个元素进行读取需要花费: 2 * k / Block_Size 个单位时间,一共有Block_Size ^ 2个元素, 一共有 (m * n) / (block_size * block_size)个Block,所以总时间就是这些值进行相乘。
因此理论加速比为Block_size,考虑到同步函数的开销以及共享内存读写的开销,实际加速比会比这个低。
四、实战代码
#include<bits/stdc++.h>
#include<sys/time.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include "cublas_v2.h"
#define M 512
#define K 512
#define N 512
#define BLOCK_SIZE 32
using namespace std;
void initial(float *array, int size){
for(int i=0;i<size;i++){
array[i] = (float)(rand() % 100 + 1);
}
}
void printMatrix(float *array,int row,int col){
float *p = array;
for(int y=0;y<row;y++){
for(int x=0;x<col;x++){
printf("%10lf",p[x]);
}
p = p + col;
printf("\n");
}
}
void multiplicateMatrixonHost(float *array_A,float *array_B,float *array_C,int M_p,int K_p,int N_p){
for(int i =0 ;i < M_p;i++){
for(int j = 0;j < N_p;j++){
float sum = 0;
for(int k = 0;k < K_p;k++){
sum += array_A[i * K_p + k] * array_B[k * N_p + j];
}
array_C[i * N_p + j] = sum;
}
}
}
__global__ void multiplicateMatrixonDevice(float *array_A,float *array_B,float *array_C,int M_p,int K_p,int N_p){
int iy = blockIdx.y * blockDim.y + threadIdx.y;
int ix = blockIdx.x * blockDim.x + threadIdx.x;
if(iy < M_p && ix < N_p){
float sum = 0;
for(int i = 0;i < K_p;i++){
sum += array_A[iy * K_p + i] * array_B[i * N_p + ix];
}
array_C[iy * N_p + ix] = sum;
}
}
//Compute C = A * B
__global__ void matrixMultiplyShared(float *A, float *B, float *C, int numARows,
int numAColumns, int numBRows,
int numBColumns, int numCRows,
int numCColumns) {
__shared__ float ds_M[BLOCK_SIZE][BLOCK_SIZE];
__shared__ float ds_N[BLOCK_SIZE][BLOCK_SIZE];
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
int Row = by * BLOCK_SIZE + ty;
int Col = bx * BLOCK_SIZE + tx;
float Pvalue = 0;
for (int m = 0; m < (numAColumns - 1) / BLOCK_SIZE + 1; ++m) {
if (Row < numARows && m * BLOCK_SIZE + tx < numAColumns) {
ds_M[ty][tx] = A[Row * numAColumns + m * BLOCK_SIZE + tx];
} else {
ds_M[ty][tx] = 0.0;
}
if (Col < numBColumns && m * BLOCK_SIZE + ty < numBRows) {
ds_N[ty][tx] = B[(m * BLOCK_SIZE + ty) * numBColumns + Col];
} else {
ds_N[ty][tx] = 0.0;
}
__syncthreads();
for (int k = 0; k < BLOCK_SIZE; ++k) {
Pvalue += ds_M[ty][k] * ds_N[k][tx];
}
__syncthreads();
}
if (Row < numCRows && Col < numCColumns) {
C[Row * numCColumns + Col] = Pvalue;
}
}
void checkResult(float *array_A,float *array_B,int size){
double epsilon = 1.0E-8;
for(int i=0;i<size;i++){
if(abs(array_A[i] - array_B[i]) > epsilon){
printf("Error! Matrix[%05d]:%0.8f != %0.8f\n",i,array_A[i],array_B[i]);
return;
}
}
printf("Check result success!\n");
}
int main(){
float *array_A,*array_B,*array_C,*array_C_host;
float *d_arrayA,*d_arrayB,*d_arrayC;
int size_A = M * K * sizeof(float);
int size_B = K * N * sizeof(float);
int size_C = M * N * sizeof(float);
array_A = (float*)malloc(size_A);
array_B = (float*)malloc(size_B);
array_C = (float*)malloc(size_C);
array_C_host = (float*)malloc(size_C);
initial(array_A,M * K);
initial(array_B,K * N);
//printMatrix(array_A,M,K);
//printMatrix(array_B,K,N);
struct timeval start,end;
gettimeofday(&start,NULL);
multiplicateMatrixonHost(array_A,array_B,array_C_host,M,K,N);
gettimeofday(&end,NULL);
cout<<"CPU time:"<<1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec<<"us"<<endl;
cudaMalloc((void**)&d_arrayA,size_A);
cudaMalloc((void**)&d_arrayB,size_B);
cudaMalloc((void**)&d_arrayC,size_C);
cudaMemcpy(d_arrayA,array_A,size_A,cudaMemcpyHostToDevice);
cudaMemcpy(d_arrayB,array_B,size_B,cudaMemcpyHostToDevice);
dim3 dimBlock(BLOCK_SIZE,BLOCK_SIZE);
dim3 dimGrid((N - 1)/ dimBlock.x + 1,(M - 1) / dimBlock.y + 1);
gettimeofday(&start,NULL);
matrixMultiplyShared<<<dimGrid,dimBlock>>>(d_arrayA,d_arrayB,d_arrayC,M,K,K,N,M,N);
gettimeofday(&end,NULL);
cout<<"GPU time:"<<1000000 * (end.tv_sec - start.tv_sec) + end.tv_usec - start.tv_usec<<"us"<<endl;
cudaMemcpy(array_C,d_arrayC,size_C,cudaMemcpyDeviceToHost);
checkResult(array_C,array_C_host,M * N);
//cout<<"Array C is :"<<endl;
//printMatrix(array_C,M,N);
cudaFree(d_arrayA);
cudaFree(d_arrayB);
cudaFree(d_arrayC);
free(array_A);
free(array_B);
free(array_C);
free(array_C_host);
return 0;
}
在这里,我着重解释一下matrixMultiplyShared函数。
这是一个利用共享内存计算矩阵乘法的 CUDA 核函数。我将逐行解释代码并在其中的 for 循环部分举一个例子。
global void matrixMultiplyShared(float *A, float *B, float *C, int numARows,
int numAColumns, int numBRows,
int numBColumns, int numCRows,
int numCColumns) {
这是一个全局函数,用于定义 CUDA 核函数。它接收两个输入矩阵 A 和 B,一个输出矩阵 C,以及与这些矩阵相关的尺寸参数。
shared float ds_M[BLOCK_SIZE][BLOCK_SIZE];
shared float ds_N[BLOCK_SIZE][BLOCK_SIZE];
定义两个共享内存数组,用于存储来自矩阵 A 和 B 的局部数据。每个数组的尺寸为 BLOCK_SIZE x BLOCK_SIZE。
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
获取当前线程所属的线程块的索引(bx,by)和线程在线程块内的索引(tx,ty)。
int Row = by * BLOCK_SIZE + ty;
int Col = bx * BLOCK_SIZE + tx;
计算当前线程所负责的输出矩阵 C 的元素的行(Row)和列(Col)。
float Pvalue = 0;
初始化累积变量 Pvalue,用于存储计算过程中的中间结果。
for (int m = 0; m < (numAColumns - 1) / BLOCK_SIZE + 1; ++m) {
外层循环用于遍历矩阵 A 和 B 的局部块。m 的上限保证了遍历所有需要的局部块。
if (Row < numARows && m * BLOCK_SIZE + tx < numAColumns) {
ds_M[ty][tx] = A[Row * numAColumns + m * BLOCK_SIZE + tx];
} else {
ds_M[ty][tx] = 0.0;
}
将矩阵 A 的局部数据加载到共享内存数组 ds_M。如果当前线程所负责的元素位于矩阵 A 的有效范围内,则从矩阵 A 中读取对应元素;否则,将 ds_M 中对应位置设为 0.0。
if (Col < numBColumns && m * BLOCK_SIZE + ty < numBRows) {
ds_N[ty][tx] = B[(m * BLOCK_SIZE + ty) * numBColumns + Col];
} else {
ds_N[ty][tx] = 0.0;
}
中读取对应元素;否则,将 ds_N 中对应位置设为 0.0。
cpp
Copy code
__syncthreads();
同步线程,确保所有线程已完成从矩阵 A 和 B 中加载数据到共享内存。
cpp
Copy code
for (int k = 0; k < BLOCK_SIZE; ++k) {
Pvalue += ds_M[ty][k] * ds_N[k][tx];
}
内层循环执行局部矩阵乘法。遍历当前线程负责的共享内存 ds_M 的一行和 ds_N 的一列,执行点乘并将结果累加到 Pvalue。
举个例子,假设 BLOCK_SIZE 为 2,那么 ds_M 和 ds_N 的尺寸都是 2x2。假设当前线程负责计算输出矩阵 C 的第一行第一列元素,即 Row 为 0,Col 为 0。那么 ty 和 tx 都是 0。在内层循环中,我们执行以下操作:
k = 0: Pvalue += ds_M[0][0] * ds_N[0][0]
k = 1: Pvalue += ds_M[0][1] * ds_N[1][0]
这样,Pvalue 就包含了 ds_M 第一行与 ds_N 第一列的点乘结果。
__syncthreads();
再次同步线程,确保所有线程已完成局部矩阵乘法,以便进行下一轮迭代。
结束外层循环。此时 Pvalue 包含了当前线程负责的输出矩阵 C 的元素所需的所有局部矩阵乘法结果。
if (Row < numCRows && Col < numCColumns) {
C[Row * numCColumns + Col] = Pvalue;
}
将 Pvalue 写入输出矩阵 C 的相应位置。如果当前线程负责的元素位于矩阵 C 的有效范围内,则将 Pvalue 写入矩阵 C。
核函数结束。
以上就是对这个并行矩阵乘法核函数的逐行解释。核心思想是将矩阵 A 和 B 分为大小为 BLOCK_SIZE x BLOCK_SIZE 的局部块,利用共享内存存储这些局部数据,然后利用线程计算局部矩阵乘法并累加结果。这种方法充分利用了 GPU 的内存层次结构,提高了计算性能。
DS_M 和 DS_N的索引方式解释
为什么在这里DS_M 和 DS_N是以这种方式进行索引的呢?
if (Row < numARows && m * BLOCK_SIZE + tx < numAColumns) {
ds_M[ty][tx] = A[Row * numAColumns + m * BLOCK_SIZE + tx];
if (Col < numBColumns && m * BLOCK_SIZE + ty < numBRows) {
ds_N[ty][tx] = B[(m * BLOCK_SIZE + ty) * numBColumns + Col];
}
这是因为矩阵 A 的元素被加载到共享内存 ds_M 中,而矩阵 B 的元素被加载到共享内存 ds_N 中。加载矩阵 A 和 B 的元素时,需要考虑到它们的不同形状以及线程和块的布局。
对于 ds_M,我们将行索引 Row 与 ty 相关联,将列索引与 m * BLOCK_SIZE + tx 相关联。以确保在加载 A 的元素时,每个线程可以从 A 中获取与其对应的元素。例如,假设 A 是一个 4x4 的矩阵,BLOCK_SIZE 是 2。那么,线程布局将如下所示:
A:
| 0 1 2 3 |
| 4 5 6 7 |
| 8 9 10 11 |
|12 13 14 15 |
Thread layout (ty, tx):
| (0, 0) (0, 1) |
| (1, 0) (1, 1) |
根据 ds_M 的索引方式,可以看到每个线程将加载 A 的元素,如下所示:
Thread (0, 0): A[0] (Row = 0, m = 0, tx = 0)
Thread (0, 1): A[1] (Row = 0, m = 0, tx = 1)
Thread (1, 0): A[4] (Row = 1, m = 0, tx = 0)
Thread (1, 1): A[5] (Row = 1, m = 0, tx = 1)
对于 ds_N,我们将行索引与 m * BLOCK_SIZE + ty 相关联,将列索引 Col 与 tx 相关联。这确保了在加载 B 的元素时,每个线程可以从 B 中获取与其对应的元素。例如,假设 B 也是一个 4x4 的矩阵,BLOCK_SIZE 是 2。那么线程布局将如下所示:
B:
| 0 1 2 3 |
| 4 5 6 7 |
| 8 9 10 11 |
|12 13 14 15 |
Thread layout (ty, tx):
| (0, 0) (0, 1) |
| (1, 0) (1, 1) |
根据 ds_N 的索引方式,可以看到每个线程将加载 B 的元素,如下所示:
Thread (0, 0): B[0] (Col = 0, m = 0, ty = 0)
Thread (0, 1): B[1] (Col = 1, m = 0, ty = 0)
Thread (1, 0): B[4] (Col = 0, m = 0, ty = 1)
Thread (1, 1): B[5] (Col = 1, m = 0, ty = 1)
通过这种方式,我们可以确保在计算局部矩阵乘法时,每个线程都可以从共享内存 ds_M 和 ds_N 中获取所需的元素。现在我们来计算局部矩阵乘法:
在这个循环中:
for (int k = 0; k < BLOCK_SIZE; ++k) {
Pvalue += ds_M[ty][k] * ds_N[k][tx];
}
每个线程计算一个 Pvalue,它是矩阵 A 的一行与矩阵 B 的一列的点积。这是一个局部矩阵乘法,因为我们在每次循环迭代时只计算 BLOCK_SIZE 大小的子矩阵。
以一个具体的例子来说明这个过程。假设我们有以下两个矩阵 A 和 B:
A: B:
| 1 2 | | 5 6 |
| 3 4 | | 7 8 |
BLOCK_SIZE 为 2,所以我们的线程布局如下:
Thread layout (ty, tx):
| (0, 0) (0, 1) |
| (1, 0) (1, 1) |
对于每个线程,我们将计算以下点积:
Thread (0, 0): Pvalue = ds_M[0][0] * ds_N[0][0] + ds_M[0][1] * ds_N[1][0] = 1 * 5 + 2 * 7 = 19
Thread (0, 1): Pvalue = ds_M[0][0] * ds_N[0][1] + ds_M[0][1] * ds_N[1][1] = 1 * 6 + 2 * 8 = 22
Thread (1, 0): Pvalue = ds_M[1][0] * ds_N[0][0] + ds_M[1][1] * ds_N[1][0] = 3 * 5 + 4 * 7 = 43
Thread (1, 1): Pvalue = ds_M[1][0] * ds_N[0][1] + ds_M[1][1] * ds_N[1][1] = 3 * 6 + 4 * 8 = 50
所以最终的结果矩阵 C 为:
C:
| 19 22 |
| 43 50 |