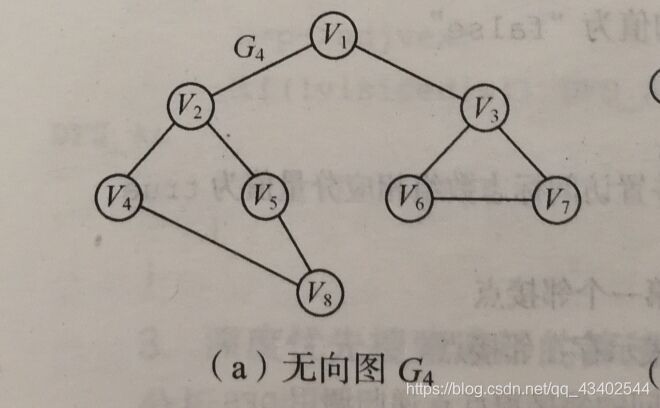
图的广度优先搜索遍历，以我的理解是：先以一个顶点做起点，一层一层的进行输出打印。
这里引用书上的一个例子。

完整代码如下（邻接表的形式）：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MVNum 100 //最大顶点数 
//创建一个中断函数 
void Interrupt(void)//创建一个中断函数 
{
	while(1)//用于检测换行符，使函数脱离scanf的连续输出 
		if(getchar()=='\n')
			break;
} 
//引入队列，这里是顺序队列 
typedef struct
{
	int data[MVNum];//分配给队列一个数组空间 
	int front;//队列头 
	int rear;//队列尾 
}SqQueue;

void InitQueue(SqQueue &Q)//初始化队列 
{
	Q.front = Q.rear = 0;//使队列头和队列尾都为0 
}

void EnQueue(SqQueue &Q,int e)//入队 ，由于是循环队列，故少用一个元素空间，该函数在有MAXSIZE-1个元素时便已判断为满 
{
	if((Q.rear+1)%MVNum == Q.front)//判断队列是否为满 ，这里是循环队列队列满的条件是 (Q.rear+1)%MAXSIZE == Q.front
	{
		printf("队列已满！\n");
	}
	else
	{
		if(Q.rear == MVNum)//如果队尾超出最大值但队列又不满，便使其对最大值求余运算 
			Q.rear = Q.rear%MVNum;
		Q.data[Q.rear] = e;//使变量e的值入队 
		Q.rear++;//并使队尾加一 
	}
}

bool QueueEmpty(SqQueue Q)//队列判空操作 
{
	if(Q.front == Q.rear)//如果队列为空，返回true，否则返回false 
		return true;
	else
		return false;
}

int DeQueue(SqQueue &Q)//出队 
{
	int a = 0;
	if(QueueEmpty(Q))//首先判断队列是否为空，队列为空的条件是 Q.front == Q.rear
		printf("队列为空！\n");
	else
	{
		a = Q.data[Q.front];//导出队头元素数据 
		Q.front++;//使队头加一 
		if(!QueueEmpty(Q))//在队列非空的情况下，如果队头等于最大值，也对最大值做求余运算 
			Q.front = Q.front%MVNum;
	}
	return a;
}
//创建矩阵表操作 
typedef struct ArcNode
{
	int adjvex;//该边所指向的顶点的位置 
	struct ArcNode *nextarc;//该向下一条边的指针 
	int weight;//权值 
}ArcNode;
typedef struct VNode//顶点信息 
{
	char data;//顶点名称 
	ArcNode *firstarc;//指向第一条依附该顶点的边的指针 
}VNode,AdjList[MVNum];//AdjList表示邻接表类型 
typedef struct//邻接表 
{
	AdjList vertices;
	int vexnum,arcnum;//图的当前顶点数和边数 
}ALGraph;

void InitGraph(ALGraph &G)//图的初始化 
{
	int i;
	for(i=0;i<MVNum;i++)
		G.vertices[i].firstarc = NULL;//使所有的第一个结点都置空，也就是后面设定的尾指针的判空操作 
}

void CreateGraph(ALGraph &G)//图的创建 
{
	int i;//记录次数 
	char a;//顶点变量 
	printf("请输入顶点数和边数:");
	scanf("%d %d",&G.vexnum,&G.arcnum);//顶点数和边数的赋值 
	Interrupt();//该函数用于检测并吸收换行符 
	printf("请输入顶点名称（连续输入）：");
	for(i=0;i<G.vexnum;i++)//利用循环输入图中顶点名称 
	{
		scanf("%c",&a);
		G.vertices[i].data = a;//第i个顶点的命名 
	}
	Interrupt();//该函数用于检测并吸收换行符
	char b,c;//顶点变量 
	int w,j,k;//w为权值变量，j和k是用来记录次数的 
	for(i=0;i<G.arcnum;i++)//利用循环输入所有边的两个顶点和权值 
	{
		printf("请输入边的两个顶点:");
		scanf("%c %c",&b,&c);//输入 
		Interrupt();//该函数用于检测并吸收换行符
		for(j=0;j<G.arcnum;j++)//该操作为书上的函数LocateVex操作 
		{
			if(G.vertices[j].data == b)//找到输入的顶点b的位置 
			break;
		}
		for(k=0;k<G.arcnum;k++)
		{
			if(G.vertices[k].data == c)//找到输入的顶点c的位置 
			break;
		}
		ArcNode *p1,*p2;//创建两个野结点 
		p1 = (ArcNode*)malloc(sizeof(ArcNode));
		p1->adjvex = k;
		p1->weight = 1;//权值赋值 
		p1->nextarc = G.vertices[j].firstarc;//类似于头插法 
		G.vertices[j].firstarc = p1;//并使头结点永远放在第一位 
		p2 = (ArcNode*)malloc(sizeof(ArcNode));
		p2->adjvex = j;
		p2->weight = 1;
		p2->nextarc = G.vertices[k].firstarc;
		G.vertices[k].firstarc = p2;
	}
}

void InputGraph(ALGraph G)//邻接表的输出 
{
	int i,j;//记录次数 
	ArcNode *p1;//用于遍历链表 
	printf("邻接表为：\n");
	for(i=0;i<G.vexnum;i++)//利用循环输出 
	{
		printf("%c",G.vertices[i].data);
		p1 = G.vertices[i].firstarc;
		while(p1)//当p为空时，结束循环 
		{
			printf(" --> %d",p1->adjvex);
			p1 = p1->nextarc;//p指向p的下一个结点 
		}	
		printf("\n");
	}
}
//广度优先搜索遍历 
ArcNode *p;//创建一个全局变量，以便于进行查找 
int FirstAdjVex(ALGraph G,int u)//表示u的第一个邻接点 
{
	p = G.vertices[u].firstarc;//全局变量的赋值 
	if(p == NULL)//如果头结点的下一个结点为空，返回负数，否则返回p结点的值 
		return -1;
	else
		return p->adjvex;
}
int NextAdjVex(ALGraph G)//下一个邻接点 
{
	p = p->nextarc;//由于p为全局变量，这里直接指向下一个便是 
	if(p == NULL)//如果头结点的下一个结点为空，返回负数，否则返回p结点的值  
		return -1;
	else
		return p->adjvex;
}
bool visited[MVNum];//访问标志数组 ,其初始值为false 
void InitVisited(bool *visited)//标志数组初始化 
{
	for(int i=0;i<MVNum;i++)
		visited[i] = false;
} 
void BFS(ALGraph G,int v)//广度优先搜索遍历 ，非递归形式 
{
	int u;
	printf("%c",G.vertices[v].data);
	visited[v] = true;//访问第v个顶点，并置访问标志数组相应分量值为true 
	SqQueue Q;
	InitQueue(Q);//引入队列，初始化 
	EnQueue(Q,v);//入队 
	while(!QueueEmpty(Q))//队列非空 
	{
		u = DeQueue(Q);//出队，别赋值给变量u 
		for(int w=FirstAdjVex(G,u);w>=0;w=NextAdjVex(G))//依次检查u的所有邻接点w,w>=0表示存邻接点
		//函数FirstAdjVex(G,u)表示u的第一个邻接点，函数NextAdjVex(G)表示相对于w的下一个邻接点 
			if(!visited[w])//w为u的尚未访问的邻接点 
			{
				printf("%c",G.vertices[w].data);
				visited[w] = true;//访问第w个顶点，并置访问标志数组相应分量值为true 
				EnQueue(Q,w);//w入队 
			}
	}
}

int main()
{
	ALGraph G;
	InitGraph(G);//初始化 
	CreateGraph(G);//邻接表的创建 
	InputGraph(G);//邻接表的输出 
	BFS(G,2);//广度优先搜索遍历 ，其中的2为测试值，可更换成变量 
	return 0;
}

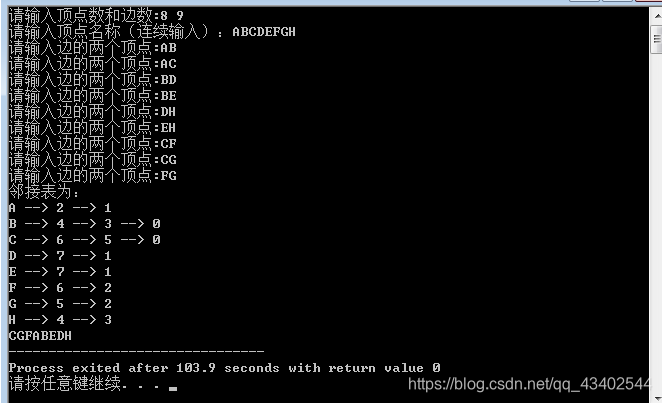
结果演示：
代码中广度优先遍历函数是从2开始输出的(也就是C)。