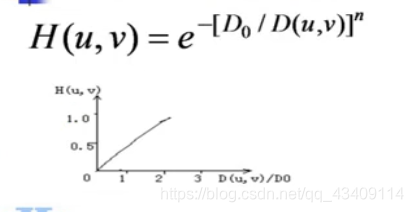本文需要用到傅里叶变换的知识，如果还不了解，请点击这里

频域滤波的基本过程

如果想对图像进行滤波的话，基本的步骤如下：

1. 使用$(-1{)}^{x+y}$乘以原来的图像，其中$x、y$是原图像的像素点的坐标。
2. 对第一步得到的数据的进行离散傅里叶变换$F(u,v)$
3. 使用某个滤波器H(u,v)乘以第三步得到的$F(u,v)$
4. 对第三步得到的结果进行傅里叶反变换，再用$(-1{)}^{x+y}$乘以反变换后的数据

下面对上面各个步骤进行解释

1. 在第一步操作中，我们对图像乘以$(-1{)}^{x+y}$是为了将频谱中心化，在中心化前，高频信号位于四个角，中心化后，高频信号都位于中心，所以这方便我们观察频谱图
2. 第二步操作就是通过离散傅里叶变换将图像转换到频率中去，其实对于滤波操作来说的化，在时域里我们也是可以进行的，只是在时域中我们要进行的是卷积操作，是非常耗时的。如果转化到频率中去，我们只需进行乘积操作就行。
3. 第三步就是用滤波器乘以图像就行了，至于为什么是乘法。点击上方链接，可以看到对傅里叶比较清晰的解释。
4. 第四步对处理后的频谱进行反变换之后就会得到第一步乘以$(-1{)}^{x+y}$以后的图像，所以我们还需要再对其乘以$(-1{)}^{x+y}$将其变换回来。

$H(u,v)$我们称其为滤波器，在变换中可以抑制或者增强某些频率而其他频率保持不变。输出图像如下：
$$G(u,v)=H(u,v)F(u,v)$$

图像在频域里面，频率低的地方说明它是比较平滑的，因为平滑的地方灰度值变化比较小，而频率高的地方通常是边缘或者噪声，因为这些地方往往是灰度值突变的
所谓高通滤波就是保留频率比较高的部分，即突出边缘；低通滤波就是保留频率比较低的地方，即平滑图像，弱化边缘，消除噪声。

在时域中的滤波器和在频域中的滤波器组成了傅里叶变换对。如果我们有时域中使用的模板等,可以通过傅里叶变换得到频域中对应的模板

下面为，对图像进行滤波处理的代码

    def PassFilter(self,H,showing=False):
        assert len(H)==self.f_height,'滤波高度不一致'
        assert len(H[0])==self.f_width,'滤波宽度不一致'
        unit=self.Img[:,:,0]
        unit_fft2=np.fft.fft2(unit)
        unit_fftshift=np.fft.fftshift(unit_fft2)
        if showing:
            img_fft_abs=10*np.log(np.abs(unit_fftshift))
            img=np.empty(shape=[self.f_height,self.f_width,3],dtype=int)
            for i in range(0, 3):
                img[:, :, i] = img_fft_abs
            plt.imshow(img)
            plt.show()

        unit_fftshift=unit_fftshift*H # 进行滤波处理

        unit_fft2_2=np.fft.ifftshift(unit_fftshift)
        unit_handle=np.fft.ifft2(unit_fft2_2)
        unit_img=np.array(np.real(unit_handle),dtype=int)
        unit_img[unit_img>255]=255
        unit_img[unit_img <0] = 0
        img = np.empty(shape=[self.f_height, self.f_width, 3], dtype=int)
        for i in range(0, 3):
            img[:, :, i] = unit_img
        self.Img=img
        print(self.Img.dtype)

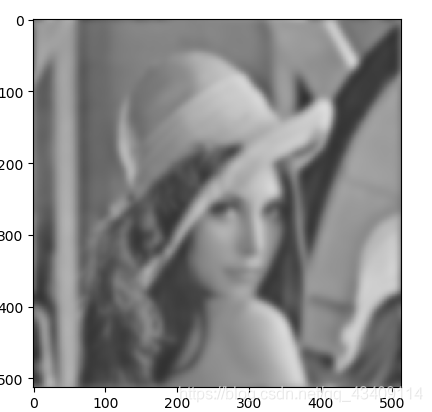
低通滤波

简单的说，就是靠近频谱图中心的低频部分给保留，远离频谱图中心的高频部分给去除掉。但是这会影响图像的清晰度。

理想低通滤波器

'生成理想低通滤波器'
def LowPass(h,w,d0,n=2):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            if d<=d0:
                H[y,x]=1
            else:
                H[y,x]=0
    return H

效果图如下

梯形滤波器

在截至频率的地方有个过渡带，会使图像显示的更好，更清晰一些

'生成梯形低通滤波器'
def TLowPass(h,w,d0,d1):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            if d<d0:
                H[y,x]=1
            elif d>d0 and d<d1:
                H[y,x]=(d1-d)/(d1-d0)
            elif d>d1:
                H[y,x]=0
    return H

效果图

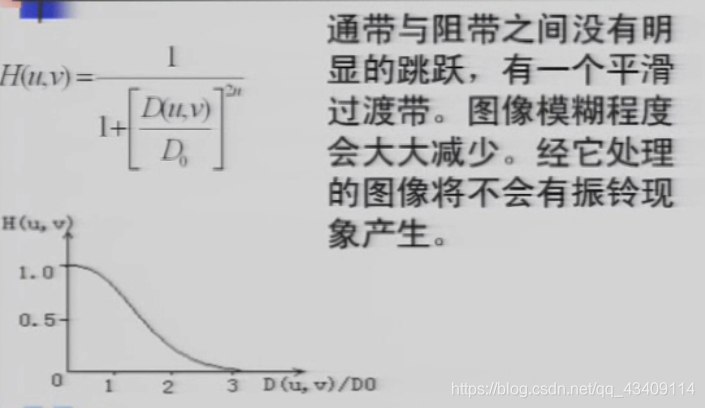
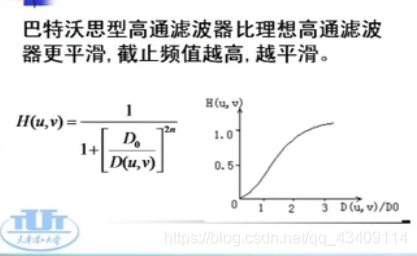
布特沃斯滤波器

'生成布特沃斯滤波器'
def ButworthLowPass(h,w,d0,n=2):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            H[y,x]=1/(1+(d/d0)**(2*n))
    return H

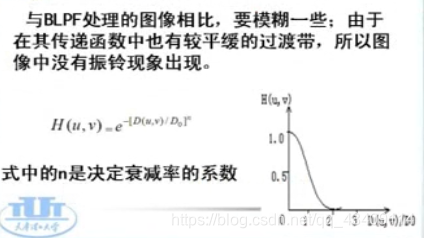
平滑特效很好，没有明显跳跃。N越大，震铃越严重。

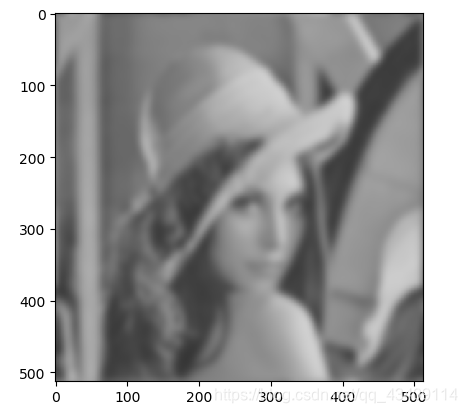
指数低通滤波器

'生成指数低通滤波器'
def IndexLowPass(h,w,d0,n=2):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            H[y,x]=np.e**(-(d/d0)**n)
    return H

效果图如下

如何确定截至频率也是非常重要的，通常可以先计算图像总功率值$P_1$，然后对某个截至频率的环内计算其环的功率值$P_2$,看看该环占总功率的百分比，根据我们的需要来选择合适的环。

$$P=\sum _{u=0}\sum _{v=0}P(u,v)(其中P(u,v)=|F(u,v){|}^2)$$

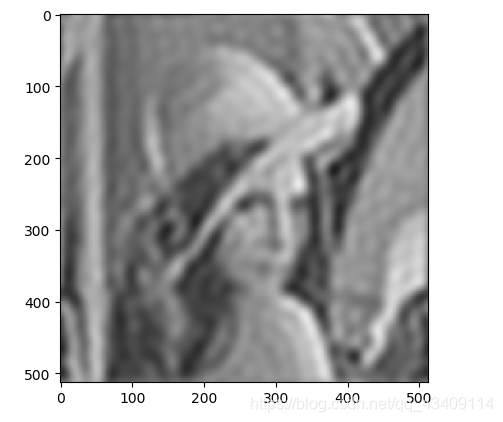
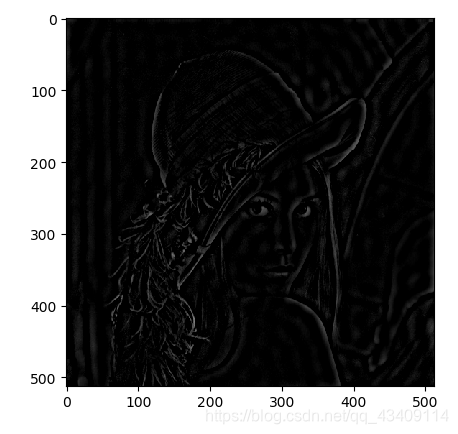
高通滤波器

简单的说，就是靠近频谱图中心的低频部分给舍弃掉，远离频谱图中心的高频部分保留。通常会保留物体的边界。

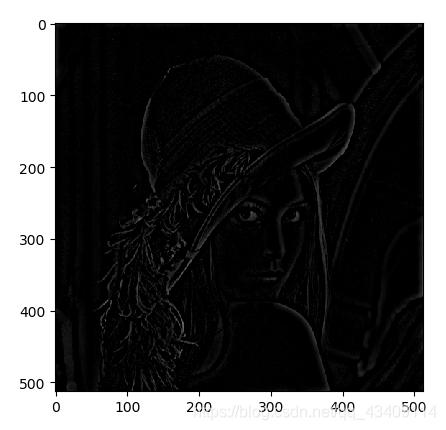
理想高通滤波器

def HighPass(h,w,d0,n=2):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            if d<=d0:
                H[y,x]=0
            else:
                H[y,x]=1
    return H

梯形高通滤波器

def THighPass(h,w,d0,d1):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            if d<d0:
                H[y,x]=0
            elif d>d0 and d<d1:
                H[y,x]=(d-d0)/(d1-d0)
            elif d>d1:
                H[y,x]=1
    return H

效果图

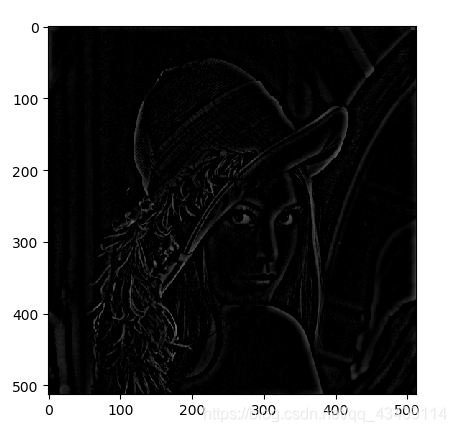
布特沃斯滤波器

'生成布特沃斯高通滤波器'
def ButworthHighPass(h,w,d0,n=2):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            H[y,x]=1/(1+(d0/(d+1))**(2*n))
    return H

效果图

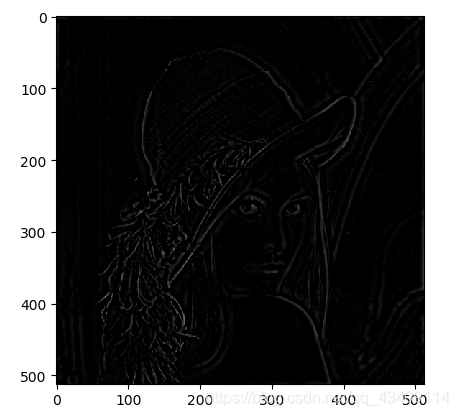
指数高通滤波器

def IndexHighPass(h,w,d0,n=2):
    H=np.empty(shape=[h,w],dtype=float)
    mid_x=int(w/2)
    mid_y=int(h/2)
    for y in range(0,h):
        for x in range(0,w):
            d=np.sqrt((x-mid_x)**2+(y-mid_y)**2)
            H[y,x]=np.e**(-(d0/(d+1))**n)
    return H

效果图

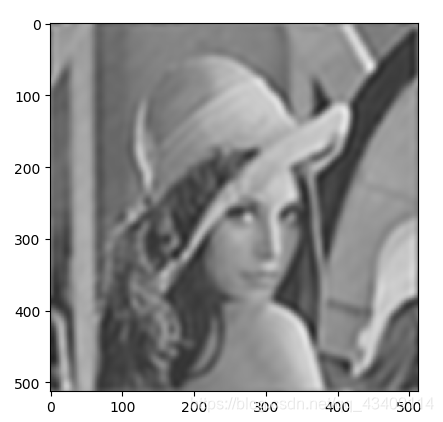
其实图像的锐化往往也可以使用高通滤波器来实现，因为锐化的时候需要加强边界，而边界部分正是高频成分

参考点击这里