LRU算法
力扣146:https://leetcode-cn.com/problems/lru-cache/
讲解视频:https://www.bilibili.com/video/BV1Hy4y1B78T?p=65&vd_source=6f347f8ae76e7f507cf6d661537966e8
LRU是Least Recently Used的缩写,是一种常用的页面置换算法,选择最近最久未使用的数据予以淘汰。(操作系统)
分析:
1 所谓缓存,必须要有读+写两个操作,按照命中率的思路考虑,写操作+读操作时间复杂度都需要为O(1)
2 特性要求分析
2.1 必须有顺序之分,以区分最近使用的和很久没用到的数据排序。
2.2 写和读操作 一次搞定。
2.3 如果容量(坑位)满了要删除最不长用的数据,每次新访问还要把新的数据插入到队头(按照业务你自己设定左右那一边是队头)
查找快,插入快,删除快,且还需要先后排序-------->什么样的数据结构满足这个问题?
你是否可以在O(1)时间复杂度内完成这两种操作?
如果一次就可以找到,你觉得什么数据结构最合适??
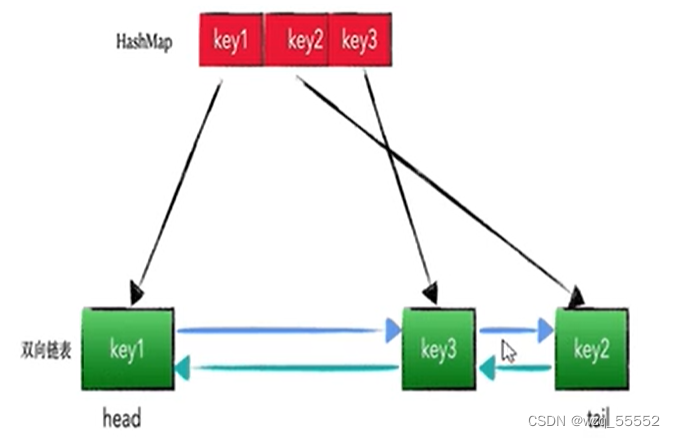
LRU的算法核心是哈希链表,本质就是HashMap+DoubleLinkedList 时间复杂度是O(1),哈希表+双向链表的结合体
利用JDK的LinkedHashMap实现:
LRU(The Least Recently Used,最近最久未使用算法)是一种常见的缓存算法,在很多分布式缓存系统(如Redis, Memcached)中都有广泛使用。
LRU算法的思想是:如果一个数据在最近一段时间没有被访问到,那么可以认为在将来它被访问的可能性也很小。因此,当空间满时,最久没有访问的数据最先被置换(淘汰)。
LRU算法的描述: 设计一种缓存结构,该结构在构造时确定大小,假设大小为 K,并有两个功能:
- set(key,value):将记录(key,value)插入该结构。当缓存满时,将最久未使用的数据置换掉。
- get(key):返回key对应的value值。
实现:最朴素的思想就是用数组+时间戳的方式,不过这样做效率较低。因此,我们可以用双向链表(LinkedList)+哈希表(HashMap)实现(链表用来表示位置,哈希表用来存储和查找),在Java里有对应的数据结构LinkedHashMap。
利用Java的LinkedHashMap用非常简单的代码来实现基于LRU算法的Cache功能,代码如下:
import java.util.LinkedHashMap;
import java.util.Map;
/**
* Title:力扣146 - LRU 缓存机制
* Description:最近最久未使用算法
* 双向链表+Hash实现,LinkedHashMap
* @author WZQ
* @version 1.0.0
* @date 2020/12/24
*/
public class LRUCache{
// 思路1 使用LinkedHashMap jdk自带
public LinkedHashMap<Integer, Integer> map;
public LRUCache(int capacity) {
// true表示纪录访问的顺序,false的话,按第一次插入的顺序不变
map = new LinkedHashMap(capacity, 0.75f, true){
// 最近最久未使用删除
@Override
protected boolean removeEldestEntry(Map.Entry eldest) {
return this.size() > capacity;
}
};
}
public int get(int key) {
return map.get(key) == null ? -1 : map.get(key);
}
public void put(int key, int value) {
map.put(key, value);
}
public static void main(String[] args) {
LRUCache lruCache = new LRUCache(3);
lruCache.put(1,"a");
lruCache.put(2,"b");
lruCache.put(3,"c");
System.out.println(lruCache.keySet());
lruCache.put(4,"d");
System.out.println(lruCache.keySet());
lruCache.put(3,"c");
System.out.println(lruCache.keySet());
lruCache.put(3,"c");
System.out.println(lruCache.keySet());
lruCache.put(3,"c");
System.out.println(lruCache.keySet());
lruCache.put(5,"x");
System.out.println(lruCache.keySet());
}
}
/**
* true
* [1, 2, 3]
* [2, 3, 4]
* [2, 4, 3]
* [2, 4, 3]
* [2, 4, 3]
* [4, 3, 5]
* false
* [1, 2, 3]
* [2, 3, 4]
* [2, 3, 4]
* [2, 3, 4]
* [2, 3, 4]
* [3, 4, 5]
*/
手写LRU:
import java.util.HashMap;
import java.util.Map;
/**
* Title:146. LRU 缓存
* Description:LRU
* @author WZQ
* @version 1.0.0
* @date 2023/2/26
*/
class LRUCache {
/**
* 数据结点
* @param <K>
* @param <V>
*/
class Node<K, V>{
K key;
V value;
Node<K, V> prev;
Node<K, V> next;
public Node() {
this.prev = this.next = null;
}
public Node(K key, V value){
this.prev = this.next = null;
this.key = key;
this.value = value;
}
}
/**
* 双端链表
* @param <K>
* @param <V>
*/
class DoubleLinkedList<K, V>{
Node<K, V> head;
Node<K, V> tail;
public DoubleLinkedList() {
// 头结点不删
head = new Node<>();
tail = new Node<>();
head.next = tail;
tail.prev = head;
}
// 头放最久未使用,尾放最新访问
// 删除节点
public void removeNode(Node<K, V> node){
node.next.prev = node.prev;
node.prev.next = node.next;
node.prev = null;
node.next = null;
}
// 添加到尾
public void addTail(Node<K, V> node){
node.prev = tail.prev;
node.next = tail;
tail.prev.next = node;
tail.prev = node;
}
// 获取最久未使用节点
public Node<K, V> getLast() {
return head.next;
}
}
private int capacity;
private DoubleLinkedList<Integer, Integer> doubleLinkedList;
private HashMap<Integer, Node<Integer, Integer>> map;
// 思路2 手写 双端链表+哈希 时间复杂度: put O(1) get O(1)
public LRUCache(int capacity) {
this.capacity = capacity;
doubleLinkedList = new DoubleLinkedList();
map = new HashMap<>();
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
Node<Integer, Integer> node = map.get(key);
doubleLinkedList.removeNode(node);
doubleLinkedList.addTail(node);
return node.value;
}
public void put(int key, int value) {
if (map.containsKey(key)){
// 已存在节点
// 删除节点,放到尾部
Node<Integer, Integer> node = map.get(key);
node.value = value;
doubleLinkedList.removeNode(node);
doubleLinkedList.addTail(node);
}else {
// 未存在节点
if (capacity == map.size()){
// 缓存数已满,需删除最久未使用
Node<Integer, Integer> last = doubleLinkedList.getLast();
doubleLinkedList.removeNode(last);
map.remove(last.key);
}
Node<Integer, Integer> node = new Node<Integer, Integer>(key, value);
doubleLinkedList.addTail(node);
map.put(key, node);
}
}
public static void main(String[] args) {
LRUCache lruCacheDemo = new LRUCache(3);
lruCacheDemo.put(1, 1);
lruCacheDemo.put(2, 2);
lruCacheDemo.put(3, 3);
System.out.println(lruCacheDemo.map.keySet());
lruCacheDemo.put(4, 1);
System.out.println(lruCacheDemo.map.keySet());
lruCacheDemo.put(3, 1);
System.out.println(lruCacheDemo.map.keySet());
lruCacheDemo.put(3, 1);
System.out.println(lruCacheDemo.map.keySet());
lruCacheDemo.put(3, 1);
System.out.println(lruCacheDemo.map.keySet());
lruCacheDemo.put(5, 1);
System.out.println(lruCacheDemo.map.keySet());
}
}
/**
[1, 2, 3]
[2, 3, 4]
[2, 3, 4]
[2, 3, 4]
[2, 3, 4]
[3, 4, 5]
*/
LFU算法
力扣:https://leetcode.cn/problems/lfu-cache/description/
LFU(Least Frequently Used ,最近最少使用算法)也是一种常见的缓存算法。
顾名思义,LFU算法的思想是:如果一个数据在最近一段时间很少被访问到,那么可以认为在将来它被访问的可能性也很小。因此,当空间满时,最小频率访问的数据最先被淘汰。如果访问频率相同,则淘汰最久未访问的。
LFU 算法的描述:
设计一种缓存结构,该结构在构造时确定大小,假设大小为 K,并有两个功能:
- set(key,value):将记录(key,value)插入该结构。当缓存满时,将访问频率最低的数据置换掉。
- get(key):返回key对应的value值。
算法实现策略:考虑到 LFU 会淘汰访问频率最小的数据,我们需要一种合适的方法按大小顺序维护数据访问的频率。LFU 算法本质上可以看做是一个 top K 问题(K = 1),即选出频率最小的元素,因此我们很容易想到可以用二项堆来选择频率最小的元素,这样的实现比较高效。最终实现策略为小顶堆+哈希表,时间复杂度O(logn),代码如下:
import java.util.Arrays;
import java.util.HashMap;
import java.util.PriorityQueue;
import java.util.TreeSet;
/**
* Title:leetcode --> 460. LFU 缓存
* Description:LFU
*
* 方法1:哈希表 + 最小堆/平衡二叉树TreeSet
* 时间复杂度:put O(logn) get O(logn) 堆运算
*
* @author WZQ
* @version 1.0.0
* @date 2023/2/26
*/
class LFUCache {
PriorityQueue<Node<Integer, Integer>> minHeap;
HashMap<Integer, Node<Integer, Integer>> map;
// 访问时间
int visitTime;
int capacity;
/**
* 数据结点
* @param <K>
* @param <V>
*/
class Node<K, V> implements Comparable<Node>{
K key;
V value;
// 访问次数
int count;
// 最新的时间,越小表示越久未访问
int lastTime;
public Node(K key, V value){
this.key = key;
this.value = value;
this.count = 1;
}
public Node(){
}
@Override
public int compareTo(Node node) {
// 访问次数一样,则取最久未访问的
return count == node.count ? lastTime - node.lastTime : count - node.count;
}
}
public LFUCache(int capacity) {
visitTime = 0;
this.capacity = capacity;
map = new HashMap<>();
minHeap = new PriorityQueue<>();
}
public int get(int key) {
if (!map.containsKey(key)){
return -1;
}
Node<Integer, Integer> node = map.get(key);
// 删除元素,重新入堆排序
minHeap.remove(node);
node.count ++;
node.lastTime = ++ visitTime;
minHeap.offer(node);
return node.value;
}
public void put(int key, int value) {
if (map.containsKey(key)){
// 访问+1,置成最新
Node<Integer, Integer> node = map.get(key);
minHeap.remove(node);
node.value = value;
node.count++;
node.lastTime = ++ visitTime;
minHeap.offer(node);
}else {
// 容量已满,剔除最小元素(最久未访问)
if (capacity == map.size()){
Node<Integer, Integer> minNode = minHeap.poll();
map.remove(minNode.key);
}
Node<Integer, Integer> node = new Node<>(key, value);
node.lastTime = ++ visitTime;
map.put(key, node);
minHeap.offer(node);
}
}
}
双hash表思路,详细可见leetcode讲解视频:https://leetcode.cn/problems/lfu-cache/solutions/186348/lfuhuan-cun-by-leetcode-solution/
时间复杂度O(1),代码如下:
import java.util.HashMap;
import java.util.Map;
/**
* Title:leetcode --> 460. LFU 缓存
* Description:LFU
*
* 双Hash表 时间复杂度 O(1)
*
* @author WZQ
* @version 1.0.0
* @date 2023/2/26
*/
class LFUCache2 {
/**
* 数据结点
* @param <K>
* @param <V>
*/
class Node<K, V>{
K key;
V value;
// 访问次数
int count;
Node<K, V> prev;
Node<K, V> next;
public Node() {
this.prev = this.next = null;
}
public Node(K key, V value){
this.prev = this.next = null;
this.key = key;
this.value = value;
count = 1;
}
}
/**
* 双端链表
* @param <K>
* @param <V>
*/
class DoubleLinkedList<K, V>{
Node<K, V> head;
Node<K, V> tail;
int size;
public DoubleLinkedList() {
// 头结点不删
head = new Node<>();
tail = new Node<>();
head.next = tail;
tail.prev = head;
size = 0;
}
// 头放最久未使用,尾放最新访问
// 删除节点
public void removeNode(Node<K, V> node){
node.next.prev = node.prev;
node.prev.next = node.next;
node.prev = null;
node.next = null;
size --;
}
// 添加到尾
public void addTail(Node<K, V> node){
node.prev = tail.prev;
node.next = tail;
tail.prev.next = node;
tail.prev = node;
size ++;
}
// 获取最久未使用节点
public Node<K, V> getLast() {
return head.next;
}
}
// key:key, value:Node节点
Map<Integer, Node<Integer, Integer>> keyTable;
// key:访问次数, value:访问次数相同的组成链表,头是最久未访问的,新的插到尾部
Map<Integer, DoubleLinkedList<Integer, Integer>> countTable;
int capacity;
int minCount;
public LFUCache2(int capacity) {
this.capacity = capacity;
keyTable = new HashMap<>();
countTable = new HashMap<>();
}
public int get(int key) {
if (!keyTable.containsKey(key)){
return -1;
}
Node<Integer, Integer> node = keyTable.get(key);
resetNode(node);
return node.value;
}
public void put(int key, int value) {
if (keyTable.containsKey(key)){
// 存在,则改变值,访问次数+1, 重置节点
Node<Integer, Integer> node = keyTable.get(key);
resetNode(node);
node.value = value;
}else {
// 容量已满,剔除最少访问节点
if (capacity == keyTable.size()){
// 通过minCount拿到最小访问的头节点(最久未访问)
Node<Integer, Integer> node = countTable.get(minCount).getLast();
keyTable.remove(node.key);
countTable.get(minCount).removeNode(node);
if (countTable.get(minCount).size == 0) {
countTable.remove(minCount);
}
}
// 新节点添加
DoubleLinkedList<Integer,Integer> linkedList = countTable.getOrDefault(1, new DoubleLinkedList());
Node<Integer, Integer> node = new Node<>(key, value);
linkedList.addTail(node);
countTable.put(1, linkedList);
keyTable.put(key, node);
minCount = 1;
}
}
/**
* 访问次数+1,重置节点在countTable的位置
* @param node
*/
public void resetNode(Node<Integer, Integer> node){
// 1. 原位置删除该节点,原位置链表为空,则删除
int count = node.count;
countTable.get(count).removeNode(node);
if (countTable.get(count).size == 0){
countTable.remove(count);
if (count == minCount) {
minCount ++;
}
}
// 2. 访问次数+1
node.count ++;
count++;
// 3. 新位置为空,则创建链表,节点添加进去
DoubleLinkedList<Integer, Integer> nextLinkedList = countTable.getOrDefault(count, new DoubleLinkedList<>());
nextLinkedList.addTail(node);
countTable.put(count, nextLinkedList);
}
}