判断题:
1-1对于一个有N个结点、K条边的森林,不能确定它共有几棵树。(F) (2分)
解析:我们假设有m棵树,假设第i棵树的节点数为ni,那么第i棵树的边数为ni-1。
那么我们可以知道(n0 - 1) + (n1 - 1) + ...... + (nm - 1) = K
因此N-m=K,于是我们可以得出结论对于n结点k条边的森林,一共有n-k棵树。
单选题:
2-1具有1102个结点的完全二叉树一定有__个叶子结点。(3分)
- 79
- 551
- 1063
- 不确定
解析:根据完全二叉树的定义我们可以知道度为1的节点最多有1个,可以没有。
于是我们假设度为0的节点数为n0,度为1的节点数为n1,度为2的节点数为n2.
于是n2+n1+n0 = 1102,并且我们知道,1101 = 2*n2+n1;
因此n1=1,并且n2 = 550,n0=551;
2-2若森林F有15条边、25个结点,则F包含树的个数是:(2分)
- 8
- 9
- 10
- 11
解析:我们根据1-1可以知道10是正确答案。
2-3将森林转换为对应的二叉树,若在二叉树中,结点u是结点v的父结点的父结点,则在原来的森林中,u和v可能具有的关系是: (3分)
1.父子关系; 2. 兄弟关系; 3. u的父结点与v的父结点是兄弟关系
- 只有2
- 1和2
- 1和3
- 1、2和3
解析:将森林转化为二叉树分为两步,第一步是将所有的树转化为二叉树,然后再将所有的二叉树转化为一棵二叉树。
也就是说当两个节点本身就是父子关系的时候(GI),原本是兄弟节点的时候(BD),在最后的二叉树当中都有两个节点都有可能是其中一个节点是另一个节点的父亲节点的父亲结点。
2-4对于一个有N个结点、K条边的森林,共有几棵树? (2分)
- N−K
- N−K+1
- N−K−1
- 不能确定
解析:同1-1
2-5设森林F中有三棵树,第一、第二、第三棵树的结点个数分别为M1,M2和M3。则与森林F对应的二叉树根结点的右子树上的结点个数是: (2分)
- M1
- M1+M2
- M2+M3
- M3
解析:第一课树的根节点就是最后的二叉树的根节点,而第二棵树的根节点是最后二叉树的右子树的根节点,而第三棵树是最后二叉树的右子树的右子树的根节点,因此四三个是正确的。
2-6由若干个二叉树组成的森林F中,叶结点总个数为N,度为2的结点总个数为M,则该集合中二叉树的个数为: (3分)
- M−N
- N−M
- N−M−1
- 无法确定
解析:我们假设有m棵二叉树。
在一棵二叉树当中我们知道n0 = n2 + 1;
因此在整个二叉树当中有N = M + m;
于是可知第二个是正确。
2-7已知一棵完全二叉树的第6层(设根为第1层)有8个叶结点,则该完全二叉树的结点个数最多是: (3分)
- 39
- 52
- 111
- 119
解析:因为第六层最多有32个结点,现在有八个叶节点,也就是说剩下的24个结点最多有48个孩子结点,因此最多就是48 + 63 = 111
2-8在一个用数组表示的完全二叉树中,如果根结点下标为1,那么下标为17和19这两个结点的最近公共祖先结点在哪里(数组下标)? (注:两个结点的“公共祖先结点”是指同时都是这两个结点祖先的结点) (3分)
- 8
- 4
- 2
- 1
解析:对于二叉树如果根节点的标号是n,那么他的左孩子的标号就是2*n,有孩子的标号就是2*n+1;
一个结点的根节点的标号就是n/2上取整。
2-9具有65个结点的完全二叉树其深度为(根的深度为1): (3分)
- 8
- 7
- 6
- 5
解析:二叉树深度与结点树的关系是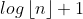
程序填空题:
下列代码的功能是计算给定二叉树T的宽度。二叉树的宽度是指各层结点数的最大值。函数Queue_rear和Queue_front分别返回当前队列Q中队尾和队首元素的位置。
typedef struct TreeNode *BinTree;
struct TreeNode
{
int Key;
BinTree Left;
BinTree Right;
};
int Width( BinTree T )
{
BinTree p;
Queue Q;
int Last, temp_width, max_width;
temp_width = max_width = 0;
Q = CreateQueue(MaxElements);
Last = Queue_rear(Q);
if ( T == NULL) return 0;
else {
Enqueue(T, Q);
while (!IsEmpty(Q)) {
p = Front_Dequeue(Q);
temp_width++;
(3分);
if ( p->Left != NULL ) Enqueue(p->Left, Q);
if ( p->Right != NULL ) Enqueue(p->Right, Q);
(3分);
if ( Queue_front(Q) > Last ) {
Last = Queue_rear(Q);
if ( temp_width > max_width ) max_width = temp_width;
temp_width = 0;
(3分);
} /* end-if */
} /* end-while */
return max_width;
} /* end-else */
} 解析:每一次更新Last指针都是一层的结束。
编程题:
7-1 树的同构 (25 分)
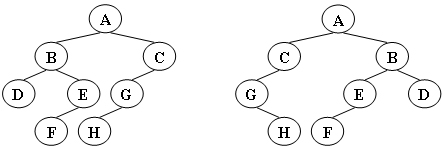
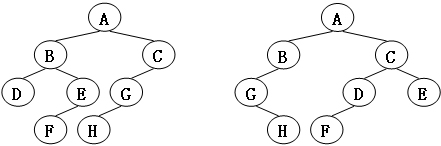
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
图1
图2
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
AC代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50 + 5;
typedef char ElemType;
struct TNode
{
ElemType data;
TNode *lch, *rch;
TNode(ElemType data = ' ', TNode *lch = nullptr, TNode *rch = nullptr) : data(data), lch(lch), rch(rch) {}
};
typedef TNode *BinTNode;
typedef TNode *BinTree;
struct Node
{
char ch;
int lch, rch;
Node(char c, char x, char y)
{
//cout << c << " " << x << " " << y << endl;
this->ch = c;
if(x != '-')
this->lch = x - '0';
else
this->lch = -1;
if(y != '-')
this->rch = y - '0';
else
this->rch = -1;
}
};
vector<Node> tree1, tree2;
bool vis1[maxn], vis2[maxn];
int n1, n2;
void read(vector<Node> &tree, bool *vis, int &n)
{
cin >> n;
for(int i = 0; i < n; i++)
{
char ch, x, y;
cin >> ch >> x >> y;
tree.push_back(Node(ch, x, y));
if(tree[tree.size() - 1].lch != -1)
vis[tree[tree.size() - 1].lch] = true;
if(tree[tree.size() - 1].rch != -1)
vis[tree[tree.size() - 1].rch] = true;
}
}
int Find(bool *vis, const int n)
{
for(int i = 0; i < n; i++)
if(!vis[i])
return i;
return -1;
}
BinTNode build(int root, const vector<Node> &tree)
{
if(root == -1)
return nullptr;
BinTNode LNode, RNode;
LNode = build(tree[root].lch, tree);
RNode = build(tree[root].rch, tree);
return new TNode(tree[root].ch, LNode, RNode);
}
void dfs(BinTNode BT)
{
if(BT == nullptr)
return ;
cout << BT->data << " ";
dfs(BT->lch);
dfs(BT->rch);
}
bool isIsomorphism(BinTNode BT1, BinTNode BT2)
{
if(BT1 == nullptr && BT2 == nullptr)
return true;
if(BT1 != nullptr && BT2 == nullptr)
return false;
if(BT1 == nullptr && BT2 != nullptr)
return false;
if(BT1->data != BT2->data)
return false;
if(isIsomorphism(BT1->lch, BT2->lch) && isIsomorphism(BT1->rch, BT2->rch))
return true;
if(isIsomorphism(BT1->lch, BT2->rch) && isIsomorphism(BT1->rch, BT2->lch))
return true;
return false;
}
int main()
{
ios::sync_with_stdio(false);
read(tree1, vis1, n1);
read(tree2, vis2, n2);
if(n1 != n2)
{
cout << "No" << endl;
return 0;
}
int root_no1 = Find(vis1, n1);
int root_no2 = Find(vis2, n2);
// cout << root_no1 << endl;
// cout << root_no2 << endl;
BinTree BT1 = build(root_no1, tree1);
BinTree BT2 = build(root_no2, tree2);
// dfs(BT1);
// cout << endl;
// dfs(BT2);
if(isIsomorphism(BT1, BT2))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
7-2 家谱处理 (30 分)
人类学研究对于家族很感兴趣,于是研究人员搜集了一些家族的家谱进行研究。实验中,使用计算机处理家谱。为了实现这个目的,研究人员将家谱转换为文本文件。下面为家谱文本文件的实例:
John
Robert
Frank
Andrew
Nancy
David
家谱文本文件中,每一行包含一个人的名字。第一行中的名字是这个家族最早的祖先。家谱仅包含最早祖先的后代,而他们的丈夫或妻子不出现在家谱中。每个人的子女比父母多缩进2个空格。以上述家谱文本文件为例,John这个家族最早的祖先,他有两个子女Robert和Nancy,Robert有两个子女Frank和Andrew,Nancy只有一个子女David。
在实验中,研究人员还收集了家庭文件,并提取了家谱中有关两个人关系的陈述语句。下面为家谱中关系的陈述语句实例:
John is the parent of Robert
Robert is a sibling of Nancy
David is a descendant of Robert
研究人员需要判断每个陈述语句是真还是假,请编写程序帮助研究人员判断。
输入格式:
输入首先给出2个正整数N(2≤N≤100)和M(≤100),其中N为家谱中名字的数量,M为家谱中陈述语句的数量,输入的每行不超过70个字符。
名字的字符串由不超过10个英文字母组成。在家谱中的第一行给出的名字前没有缩进空格。家谱中的其他名字至少缩进2个空格,即他们是家谱中最早祖先(第一行给出的名字)的后代,且如果家谱中一个名字前缩进k个空格,则下一行中名字至多缩进k+2个空格。
在一个家谱中同样的名字不会出现两次,且家谱中没有出现的名字不会出现在陈述语句中。每句陈述语句格式如下,其中X和Y为家谱中的不同名字:
X is a child of Y
X is the parent of Y
X is a sibling of Y
X is a descendant of Y
X is an ancestor of Y
输出格式:
对于测试用例中的每句陈述语句,在一行中输出True,如果陈述为真,或False,如果陈述为假。
输入样例:
6 5
John
Robert
Frank
Andrew
Nancy
David
Robert is a child of John
Robert is an ancestor of Andrew
Robert is a sibling of Nancy
Nancy is the parent of Frank
John is a descendant of Andrew
输出样例:
True
True
True
False
FalseAC代码:
#include <bits/stdc++.h>
using namespace std;
struct Node
{
string name;
int level;
vector<Node *> child;
Node *father;
Node(string name) : name(name) {}
};
typedef Node *TNode;
typedef Node *Tree;
Tree tree;
struct Person
{
string name;
int level;
Person(string name, int level) : name(name), level(level) {}
};
vector<Person> people;
int n, m;
int getlevel(string name)
{
int ans = 0;
while(name[ans++] == ' ')
;
return ans;
}
void read()
{
cin >> n >> m;
getchar();
for(int i = 0; i < n; i++)
{
string str, x;
getline(cin, str);
//cout << "str = " << str << endl;
int level = getlevel(str);
stringstream ss(str);
ss >> x;
people.push_back(Person(x, level));
}
}
TNode build(int dp, TNode Father)
{
TNode node = new Node(people[dp].name);
node->father = Father;
for(int i = dp + 1; i < people.size() ;i++)
{
if(people[i].level == people[dp].level + 2)
node->child.push_back(build(i, node));
if(people[i].level == people[dp].level)
break;
}
return node;
}
TNode FindNode(string name, TNode Root)
{
if(name == Root->name)
return Root;
for(int i = 0; i < Root->child.size(); i++)
{
TNode temp = FindNode(name, Root->child[i]);
if(temp == nullptr)
continue;
if(temp->name == name)
return temp;
}
return nullptr;
}
void bfs(TNode T)
{
queue<TNode> que;
que.push(T);
while(!que.empty())
{
TNode temp = que.front();
que.pop();
cout << "my name is " << temp->name;
if(temp->father != nullptr)
cout << " my father name is " << temp->father->name;
cout << endl;
for(int i = 0; i < temp->child.size(); i++)
que.push(temp->child[i]);
}
}
bool isChild(TNode child_node, TNode parent_node)
{
if(child_node->father != nullptr)
return child_node->father->name == parent_node->name;
return false;
}
bool isAncestor(TNode ancester_node, TNode child_node)
{
// cout << ancester_node->name << endl;
// cout << child_node->name << endl;
while(child_node->father != nullptr)
{
if(child_node->father->name == ancester_node->name)
return true;
child_node = child_node->father;
}
return false;
}
bool isSibling(TNode brother_node, TNode sister_node)
{
if(brother_node->father != nullptr && sister_node->father != nullptr)
return brother_node->father->name == sister_node->father->name;
return false;
}
bool isParent(TNode parent_node, TNode child_node)
{
return isChild(child_node, parent_node);
}
bool isDecendant(TNode child_node, TNode grand_node)
{
return isAncestor(grand_node, child_node);
}
int main()
{
read();
tree = build(0, nullptr);
//bfs(tree);
for(int i = 0; i < m; i++)
{
string str[6];
for(int j = 0; j < 6; j++)
cin >> str[j];
TNode first_node = FindNode(str[0], tree);
TNode second_node = FindNode(str[5], tree);
// cout << first_node->name << endl;
// cout << second_node->name << endl;
if(first_node == nullptr || second_node == nullptr)
{
cout << "False" << endl;
continue;
}
if(str[3] == "child")
{
if(isChild(first_node, second_node))
cout << "True" << endl;
else
cout << "False" << endl;
}
else if(str[3] == "ancestor")
{
if(isAncestor(first_node, second_node))
cout << "True" << endl;
else
cout << "False" << endl;
}
else if(str[3] == "sibling")
{
if(isSibling(first_node, second_node))
cout << "True" << endl;
else
cout << "False" << endl;
}
else if(str[3] == "parent")
{
if(isParent(first_node, second_node))
cout << "True" << endl;
else
cout << "False" << endl;
}
else if(str[3] == "descendant")
{
if(isDecendant(first_node, second_node))
cout << "True" << endl;
else
cout << "False" << endl;
}
}
return 0;
}