线性表概念
线性表(List):零个或多个数据元素的有限序列
线性表的抽象数据类型
ADT 线性表
Data
线性表的数据对象集合为(a1,a2,.....an),每个元素的类型均为DataType。其中,除第一个元素a1外
每个元素有且只有一个直接前驱元素,除了最后一个元素an外,每一个元素都有且只有一个直接后继元素。数据元素
之间的关系是一对一的关系。
Operation
InitList(*L) 初始化操作,建立一个空的线性表
ListEmpty(L) 若线性表为空,返回true,否则返回false
ClearList(*L) 将线性表清空
GetElem(L,i,*e) 将线性表中的第i个位置元素返回给e
LocateElem(L,e) 在线性表L中查找与给定值e相等的元素,如果查找成功,返回该元素在表中的序号
表示成功,否则返回0表示失败
ListInsert(*L,i,e) 在线性表中的第i个位置插入新元素e
ListDelete(*L,i,*e) 删除线性表L中第i个位置元素,并用返回值e返回其值
ListLength(L) 返回线性表L的元素个数
endADT线性表的顺序存储结构
顺序存储定义
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。
线性表(a1,a2,......an)的顺序存储结构如下:

举个例子,有个同学,人特别老实,热心,经常帮室友去图书馆占座,他总是答应,如果一个宿舍九个人,他每一次吃完早饭,就冲去图书馆,挑一个好地,把他书包里的书一本一本的按座位放好,这里连续的九个位置就相当于是一个顺序存储结构。
顺序存储方式
线性表的顺序存储结构,说白了和上面的例子一样,就是在内存中找了块地方,通过占位的形式,把一定内存空间给占了,然后把相同数据类型的数据元素依次存放在这块空地中,既然线性表的每个数据元素类型都相同,所以可以用C语言(其他语言也相同)的一维数组来实现顺序存储结构,即把第一个数据元素存到数组下标为0的位置中,接着把线性表相邻的元素存储到数组中相邻的位置。
可以看下,线性表的顺序存储结构代码
#define MAXSIZE 20 /*存储空间初始分配量*/
typedef int Elemtype /*Elemtype类型根据实际情况而定,这里假设为int*/
typedef struct
{
Elemtype data[MAXSIZE]; /*数组存储数据元素,最大值为MAXSIZE*/
int length; /*线性表当前长度*/
}Sqlist;这里,我们可以发现描述顺序存储结构需要三个属性
存储空间的起始位置:数组data,它的存储位置就是存储空间的存储位置
线性表的最大存储容量:数组长度MaxSize
线性表的当前长度:length
数据长度和线性表长度的区别
数组的长度:是存放线性表的存储空间的长度,存储分配后这个量一般是不变的,其实数组长度也可以变化,动态分配一维数组和柔性数组可以是不定长的数组。
线性表的长度:是线性表中数据元素的个数,随着线性表插入和删除操作的进行,这个量是变化的。
在任意时刻,线性表的长度小于等于数组的长度。
地址计算方法
由于我们的数都是从1开始数的,线性表的定义也不能免俗,起始也是1,可C语言的数组却是从0开始第一个下标的,于是线性表的第i个元素是要存储在数组下标为i-1的位置,即数据元素的序号和存放它的数组下标之间存在对应关系:
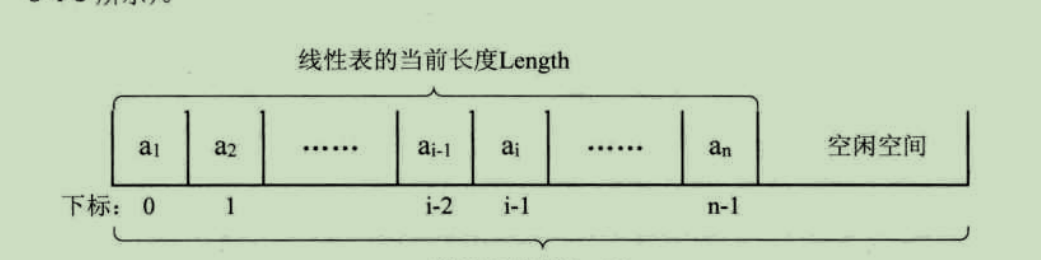
用数组存储顺序表意味着要分配固定长度的数组空间,由于线性表中可以插入和删除操作,因此分配的数组空间要大于当前线性表的长度。
其实,内存中的地址,就和图书馆里或者电影院里的座位一样,都是有编号的。存储器中的每个存储单元都有自己的编号,这个编号称之为地址。
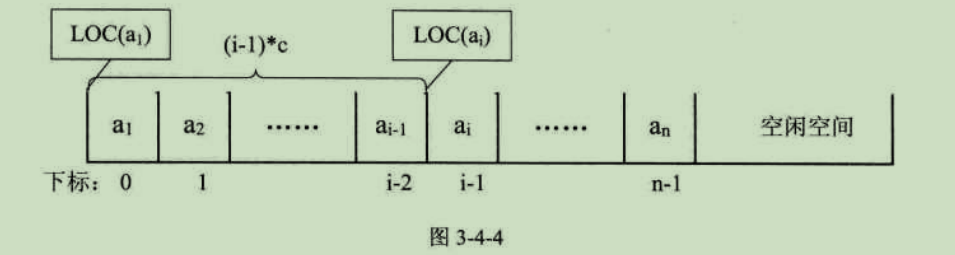
LOC(ai+1) = LOC(ai) + c
所以对于第i个数据元素ai可以由a1推算得出:
LOC(ai) = LOC(a1) + (i-1)*c
顺序存储结构的操作
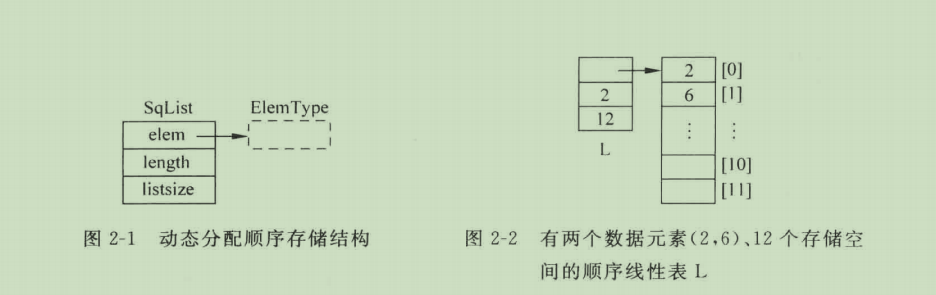
线性表的动态分配顺序存储结构
#define LIST_INIT_SIZE 10 //线性表存储空间的初始分配量
#define LIST_INCREMENT 2 //线性表的存储空间的分配增量
struct SqList
{
Elemtype *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(Elemtype)为单位
}其实,可以不采用固定数组作为线性表的存储结构,而是采用动态分配的存储结构,这样可以合理的利用空间,使长表占用的存储空间多,短表占用的存储空间少,这样内存的分配更加灵活。
初始化线性表
void InitList(SqList *L)
{
L->elem = (Elemtype *)malloc(sizeof(Elemtype) * length);
if(L->elem == NULL)
{
exit(OVERFLOW);
}
L->length = 0; //空表长度为0
L->listsize = LIST_INIT_SIZE; //初始存储容量
}销毁线性表
void Destroy(SqList *L)
{
//初始条件:顺序线性表已经存在,操作结果:销毁顺序线性表
free(L->elem); //释放L->elem所指向的存储空间
L->elem = NULL; //L->elem不再指向任何存储单元
L—>length = 0;
L->listsize = 0;
}清空线性表
void ClearList(SqList *L)
{
//初始条件:顺序线性表已经存在,操作结果:将L重置为空表
L->length = 0;
}判断线性表是否为空
Status ListEmpty(SqList *L)
{
//初始条件:顺序线性表已经存在
if(L->length = 0)
{
return TRUE;
}
else
return FALSE;
}求线性表的长度
int ListLength(SqList *L)
{
//初始条件:顺序线性表L已存在,操作结果:返回L中数据元素个数
return L->length;
}获取指定位置的元素
Status Get_List_sq(List_sq List_sq, int pos, Elemtype *elem)
{
if(is_empty_Listsq(List_sq)) //判断线性表是否为空
{
return ERROR;
}
if(pos<1||pos>List_sq->cnt) //指定的位置是否合理
{
return ERROR;
}
// elem->name = (char *)malloc(sizeof(char)*LENGTH);
//elem->number = (char *)malloc(sizeof(char)* LENGTH);
{
elem->name = List_sq->elem[pos-1].name;
elem->number = List_sq->elem[pos-1].number;
elem->age = List_sq->elem[pos-1].age; //这里我是元素的类型,是一个结构体,包含姓名和学号和年龄,前两者是char *后者是int
return OK;
}
}查找某个元素在线性表中的位置
Status Locate_List_sq(List_sq List_sq, char **name) //根据元素的姓名成员查找
{
if(is_empty_Listsq(List_sq))
{
return ERROR;
}
else
{
for(int i=0; i<List_sq->cnt; i++)
{
if(strcmp(List_sq->elem[i].name,*name) == 0)
{
return i+1;
}
}
return ERROR;
}
}
这下面是参考别人的代码
int LocateElem(SqList L, Elemtype e, Status (*compare)(Elemtype, Elemtype))
{
//初始条件:顺序线性表L已存在,compare是数据元素判定函数(满足为1,否则为0)
//操作结果:返回L中第一个与e满足关系compare()的 数据元素的位置
如果不存在则返回0
int i=1;
Elemtype *p = L.elem; //p的初值为第一个元素的存储位置
while(i<= L.length!=compare(*p++,e)) //i未超出表的范围且未找到满足关系的数据元素
i++;
if(i<L.length)
{
return i; //找到满足关系的数据元素
}
else
{
return 0; //未找到,返回0
}
}这里个人觉得,后者的代码精妙之处在于是用来函数指针,通过函数指针可以修改根据什么条件来查找,这是非常精妙的一个地方。
获取前一个元素
Status PriorElem(SqList L, Elemtype cur_e, Elemtype *pre_e)
{
int i = 2;
Elemtype *p = L.elem+1; //p指向第二个元素
while(i<=L.length&&*p!=cur_e) //i未超出表的范围且未找到值为cur_e的元素
{
p++; //p指向下一个元素
i++; //计数加1
}
if(i>L.length) //到表结束处还未找到值为cur_e的元素
return ERROR;
else
{ //找到了
pre_e = *--p;
return OK;
}
}找元素的下一个元素
Status NextElem(SqList L,Elemtype cur_e,Elemtype *next_e)
{
int i=1;
Elemtype *p = L.elem;
while(i<L.length&&*p!=cur_e)
{
p++;
i++;
}
if(I==L.length)
return ERROR;
else
{
next_e = *++p;
return OK;
}
}插入元素
举个例子,本来我们在春运时去买火车票,大家都排队排的好好的。这时来了一个美女,对着队伍中排在第三位的你说,“大哥,求求你帮帮忙,我家母亲有病,我得急着回去看她,这队伍这么长,你可否让我排在你的前面?”你心一软,就同意了。这时,你必须得退后一步,否则她是没法进到队伍来的。这可不得了,后面的人像蠕虫一样,全部都得退一步。骂起四声。但后面的人也不清楚这加塞是怎么回事,没什么办法。
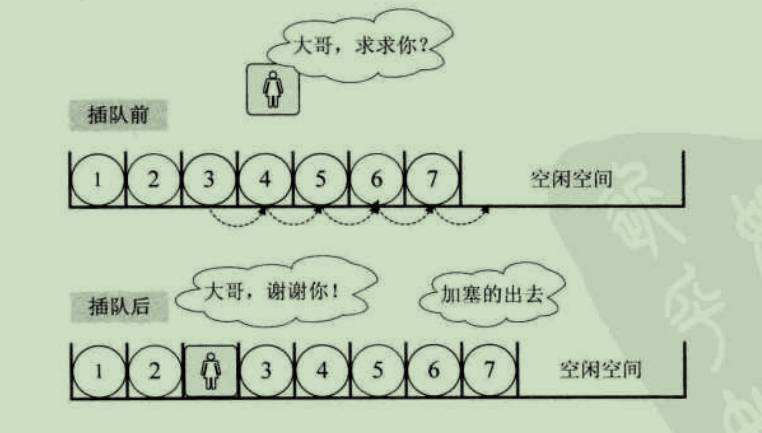
插入算法的思路:
如果插入位置不合理,抛出异常
如果线性表的长度大于等于数组长度,则抛出异常或动态增加容量
从最后一个元素开始向前遍历到第i个位置,分别将他们都向后移动一个位置
将要插入元素填入位置i处
表长加1
Status ListInsert(SqList *L,int i,Elemtype e)
{
Elemtype *newbase,*p,*q;
if(i<1||i>L->length+1) //插入位置是否合法
return ERROR;
if(L->length == L.listsize) //表是否已满
{
newbase = (Elemtype *)realloc(L->elem,(L->listsize + LIST_INCREMENT)*sizeof(Elemtype));
if(!newbase)
exit(OVERFLOW);
L->elem = newbase; //新基址赋给L->elem
L->listsize += LIST_INCREMENT; //增加存储容量
}
q = L->elem + i -1; //q为插入位置
for(p = L->elem + L->length -1;p>=q;--p) //插入位置及之后的元素右移(由表尾元素开始移)
*(p+1) = p;
*q = e;
L->length++;
return OK;
}删除元素操作
可以接着刚才的例子,此时后面排队的人群意见都很大,都说怎么可以这样,不管什么原因,插队就是不行,有本事找火车站开后门去,就这时,远处跑来一胖子,对着这美女大喊,可找到你了,你这骗子,还我钱。只见这女子二话不说,突然就冲出了队伍,胖子追在其后,消失在人群中。哦,原来她是倒卖火车票的黄牛,刚才还装可怜。于是排队的人群,又像蠕虫一样开始往前移动一步,骂声渐渐消失,队伍又恢复了平静。
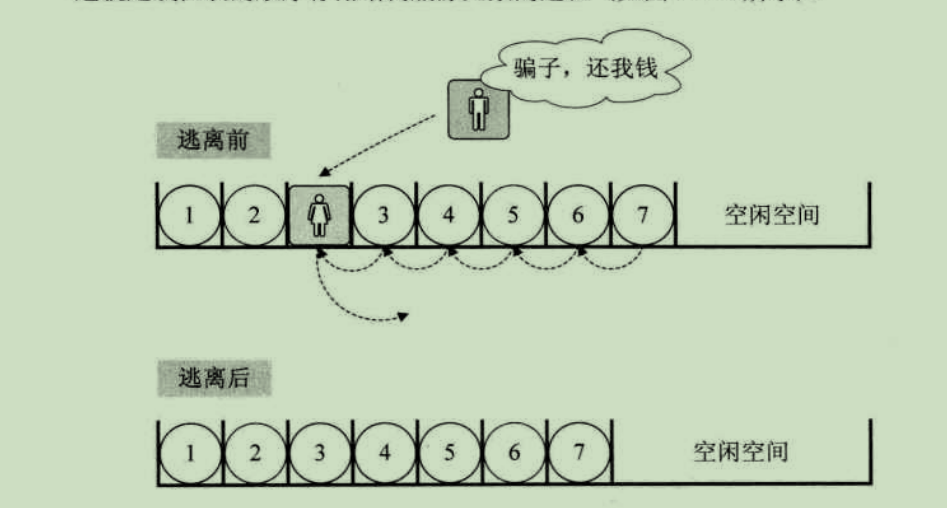
删除算法的思路:
如果删除位置不合理,抛出异常
取出删除元素
从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置
表长减1
Status ListDelete(SqList *L,int i,Elemtype *e)
{
int k;
if(L->length == 0) /*线性表为空*/
return ERROR;
if(i<1||i>L->length)
{
return ERROR; /*删除位置不合理*/
}
*e = L->data[i-1];
if(i<L->length) /*如果删除位置不是最后一个位置*/
{
for(k = i;k<L->length;k++)
{
L->data[k-1] = L->data[k]; //将删除位置后继元素前移
}
}
L->length--;
return OK;
}线性表顺序存储结构的优缺点
优点:
无须为表示表中元素之间的逻辑关系而增加 额外的空间
可以快速的存取表中任意位置的元素
缺点
插入和删除操作需要移动大量的元素
当线性表长度变化较大时,难以确定存储空间的容量
造成存储空间的“碎片”
线性表的链式存储结构
为了表示每个数据元素ai与其直接后继ai+1之间的逻辑关系,对于数据元素ai来说,除了存储其本身的信息之外,还需存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域,把存储直接后继的域称作指针域。指针域中存储信息的称作指针或链,这两部分信息组成元素ai的存储映像,称作结点node。
n个结点(ai的存储映像)链接成一个链表,即为线性表(a1,a2,....an)的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。
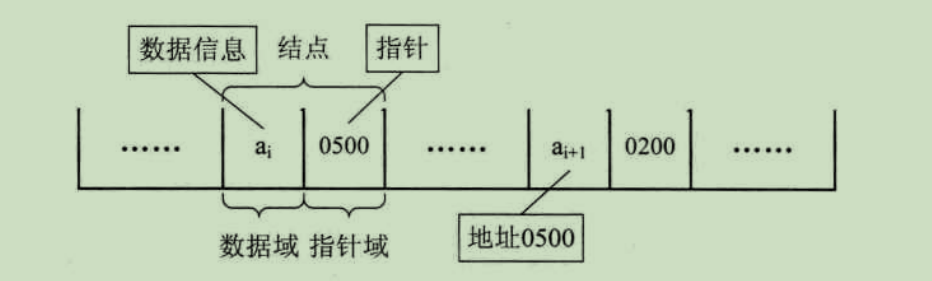
对于线性表来说,总得有个头有个尾,链表也不例外,我们把链表中第一个结点的存储位置叫做头指针,那么整个链表的存取就必须是从头指针开始进行了。最后一个,当然意味着直接后继不存在,通常结点指针为空,用NULL表示。
有时,为了方便对链表的操作,会在单链表的第一个结点前附设一个结点,称为头结点。头结点的数据域可以存储信息,也可以不存储任何信息,头结点的指针指向第一个结点的指针。
头结点和头指针的异同
头指针:
头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针
头指针具有标识作用,所以常用头指针冠以链表名字
无论链表是否为空,头指针均不为空,头指针是链表的必要元素
头结点:
头结点是为了操作的统一和方便而设立的,放在第一元素的结点之前,其数据域一般无意义(也可存放链表的长度)
有了头结点,对第一元素结点前插入结点和删除第一结点,其操作与其它节点的操作就统一了
头结点不一定是链表必须要素
线性表链式存储结构代码描述
若线性表为空,则头结点的指针域为空,
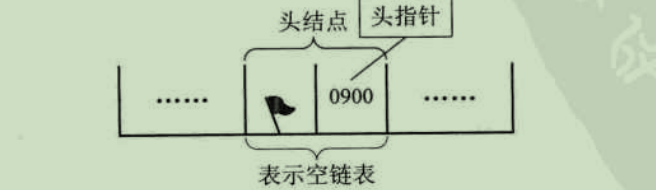
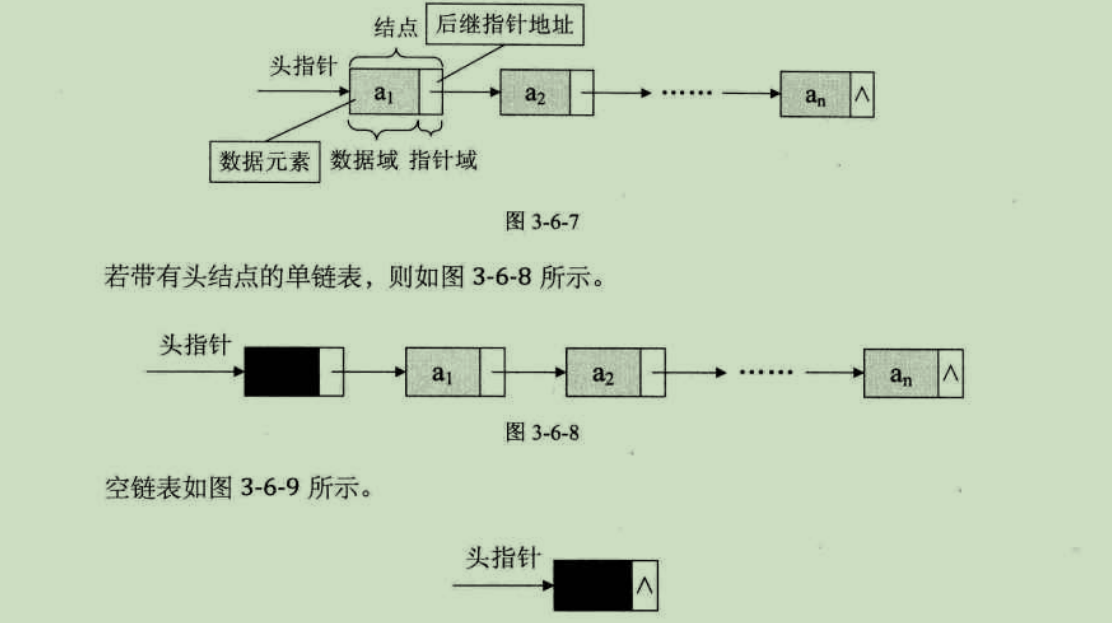
线性表的单链表存储结构
struct LNode{
Elemtype data;
LNode *next;
}
typedef LNode *LinkList; 以下操作都是针对有头结点的链表:
初始化链表
void InitList(LinkList *L)
{
L = (LinkList)malloc(sizeof(LNode));
if(!L)
exit(OVERFLOW);
L->next = NULL; //头结点指针域为空
}销毁链表
void Destroy(LinkList *L)
{
LinkList q;
while(L) //L指向
{
q = L->next; //q指向首元结点
free(L); //释放头结点
L=q; //L指向首元结点,现头结点
}
}清空链表
void ClearList(LinkList L)
{
LinkList p = L->next; //p指向第一个结点
L->next = NULL; //头结点指针域为空
Destroy(p); //销毁p所指的单链表
}判断链表是否为空
Status ListEmpty(LinkList L)
{
if(L->next) //非空
return FALSE:
else
return TRUE;
}求链表长度
int ListLength(LinkList L)
{
int i=0; //计数器初值
LinkList p = L->next; //p指向第一个结点
while(p)
{
i++; //依次遍历,计数
p = p->next;
}
return i;
}获取元素
Status GetElem(LinkList L,int i,Elemtype *e)
{
int j=1; //计数器初值为1
LinkList p = L->next; //p指向第一个结点
while(p&&j<i) //顺着指针往后查找,直到p指向第i个结点或p成为空(第i个结点不存在)
{
j++; //计数器加1
p=p->next; //p指向下一个结点
}
if(!p||j>i) //第i个结点不存在
return ERROR;
*e = p->data; //取第i个元素的值赋给e
return OK;
}查找某个元素的位置
int LocateElem(LinkList L,Elemtype e, Status (*compare)(Elemtype,Elemtype))
{
int i=0;
LinkList p=L->next;
while(p)
{
i++;
if(compare(p->data,e))
return i;
p=p->next;
}
return 0;
}插入新结点
Status ListInsert(LinkList L,int i,Elemtype e)
{
int j=0;
LinkList s,p=L;
while(p&&j<i-1) //寻找第i-1个结点
{
j++;
p=p->next;
}
if(!p||j>i-1) //i小于1或者大于表长
{
return ERROR;
}
s = (LinkList)malloc(sizeof(LNode)); //生成新结点,以下将其插入L中
s->data = e; //将e赋值给新结点
s->next = p->next; //新结点指向原第i个结点
p->next=s; //原第i-1个结点指向新结点
return OK;
}删除结点
Status ListDelete(LinkList L,int i,Elemtype *e)
{
int j=0;
LinkList q,p=L;
while(p->next&&j<i-1) //寻找第i个结点,并令p指向其前趋
{
j++;
p=p->next;
}
if(!p->next||j>i-1) //删除位置不合理
{
return ERROR; //删除失败
}
q = p->next;
p->next = q->next;
e = q->data;
free(q);
return OK;
}个人总结
数据结构中最基本的线性表,分为顺序存储结构和链式存储结构,其中不同的存储结构,其相同操作具体实现是不一样的,更加充分证明了数据结构是研究数据类型和存储结构的一门课程,这里代码难点在于指针的灵活运用和函数指针的画龙点睛之用,具体操作是只有懂了原理不算特别难,自己手敲实现了顺序表和链表的一些简单操作:可以参考
(3条消息) 数据结构——线性表_~Old的博客-CSDN博客
具体操作难点就在于插入和删除操作