Bootstrap

二叉查找树（Binary Search Tree）Java语言实现

一、二叉查找树

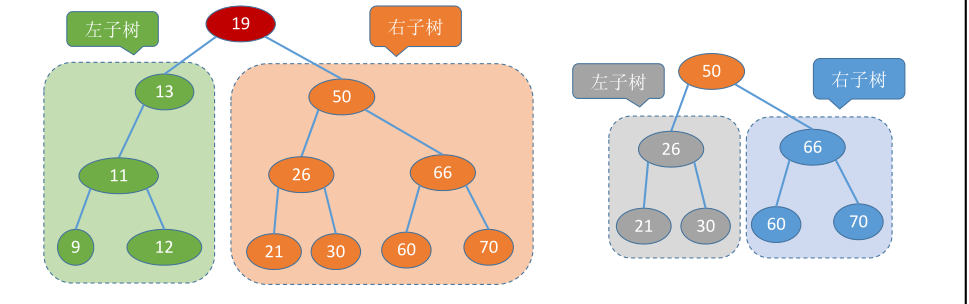
二叉查找树（Binary Search Tree），也称为二叉搜索树、有序二叉树（Ordered Binary Tree）或排序二叉树（Sorted Binary Tree）。

是指一棵空树或者具有下列性质的二叉树：

  1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
  3. 任意节点的左、右子树也分别为二叉查找树；

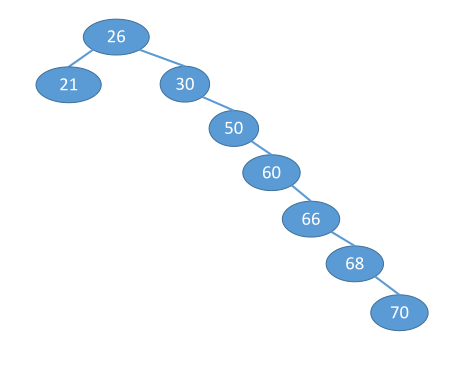
下图即为一个二叉查找树：
在这里插入图片描述

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低，为O(log⁡n)。

二叉查找树的左子树结点值小于根结点值小于右子树结点值特点，使得其中序遍历的结果始终为顺序的。

二、二叉查找树的操作

1. 二叉搜索树的查找

根据二叉搜索树的特性依次比较val与各个节点值的大小，从而查找与val相等的节点。

在二叉查找树b中查找val的过程为：
step1. 若b是空树，则搜索失败：
step 2. 若val等于b的根节点的数据域之值，则查找成功；
step 3. 若val小于b的根节点的数据域之值，则搜索左子树；若val小于b的根节点的数据域之值，则搜索右子树

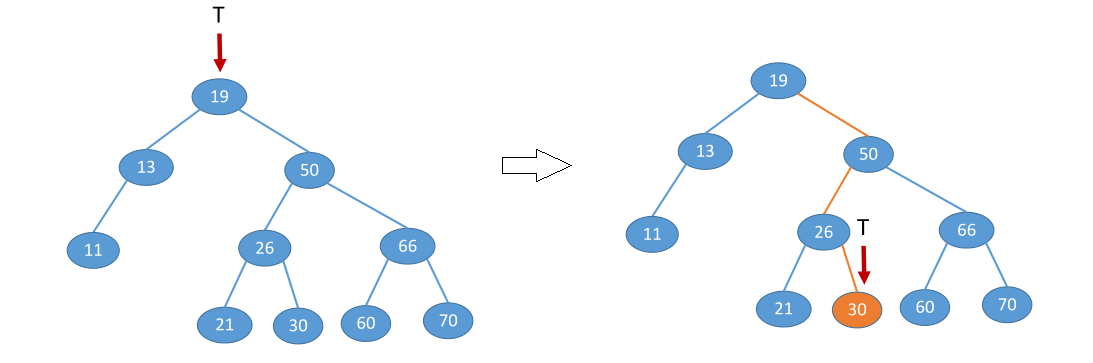
例1：查找关键字为30的结点
（1）首先从根节点19开始，发现19 小于 30，所以对以50作为根节点的右子树进行下一轮搜索；
（2）然后以此右子树为基准继续查找，发现50 大于 30，所以对以26作为根节点的左子树进行下一轮搜索；
（3）然后以此左子树为基准继续查找，发现26 小于 30，所以对以30作为根节点的右子树进行下一轮搜索；
（4）最后以此右子树为基准继续查找，发现30 等于 30，查找成功。
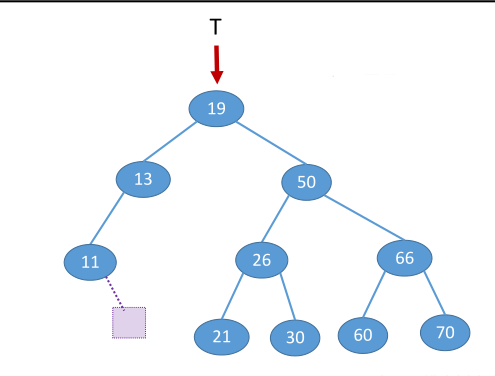
在这里插入图片描述
例2：查找关键字为12的结点
（1）首先从根节点19开始，发现19 大于 12，所以对以13作为根节点的左子树进行下一轮搜索；
（2）然后以此左子树为基准继续查找，发现11 小于 30，但是11是叶子结点，即它没有右子树，所以判断出该二叉排序树中没有值为12的节点，搜索失败。

在这里插入图片描述
示例代码如下：

    public void get(int val) {
    	TreeNode currentNode = root;
    	TreeNode findTreeNode = new TreeNode();
    	while (currentNode != null) {
			if (currentNode.val > val) { // 当前节点比将要插入的值大
				currentNode = currentNode.left; // 去根节点左子树中继续寻找
			} else if (currentNode.val < val) { // 当前节点比将要插入的值小
				currentNode = currentNode.right; // 去根节点右子树中继续寻找
			} else if (currentNode.val == val)  {
				findTreeNode = currentNode; //相等，则currentNode是要寻找的节点。
				System.out.println(findTreeNode.val + " has been found!");
				return;
			}
    	}
    	System.out.println("Error! " + val + " does not exist!");
    }

2.在二叉搜索树中插入节点

要插入节点，必须先找到插入的位置。由于二叉搜索树的特殊性，待插入的节点需要从根节点开始进行比较。小于根节点则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空，则插入到相应为空的位置。

在比较的过程中要注意保存父节点的信息及待插入的位置是父节点的左子树还是右子树。

将val插入到二叉搜索树r的具体流程如下：
step1.若二叉搜索树r是空树，则将val所指节点作为根节点插入；
step2.若val等于二叉搜索树r的根节点的值，则返回“val已经存在于该二叉搜索树中”；
step3.若val小于二叉搜索树r的根节点的值，则将左子树作为下一轮的根节点并返回step1；若val大于二叉搜索树的根节点的值，则将左子树作为下一轮的根节点并返回step1。（新插入节点总是叶子节点）

例：插入关键字为12的结点（新插入的节点一定是叶子结点）
在这里插入图片描述

    public void insert(int val) {
    	TreeNode treeNode = new TreeNode();
    	treeNode.val = val;
    	if (root == null) { // 如果根节点为空，说明是个空树
    		root = treeNode;
    		System.out.println(val + " has been inserted into the binary tree!");
    	} else {
    		TreeNode currentNode = root; // 要插入位置的节点，初始为root，从根节点依次寻找
			TreeNode parentNode = null; // 要插入位置的父节点
    		while (currentNode != null) {
    			parentNode = currentNode;
    			if (currentNode.val > val) { // 当前节点比将要插入的值大
    				currentNode = currentNode.left; // 与根节点左子树比较
    				if (currentNode == null) { // 若左节点为空 则直接插入即可
    					parentNode.left = treeNode;
    					System.out.println(val + " has been inserted into the binary tree!");
    					break;
    				}	
    			} else if (currentNode.val < val) { // 当前节点比将要插入的值小
    				currentNode = currentNode.right; // 与根节点右子树比较
    				if (currentNode == null) { // 若右节点为空 则直接插入即可
    					parentNode.right = treeNode;
    					System.out.println(val + " has been inserted into the binary tree!");
    					break;
    				}
    			} else {
    				System.out.println(val + " repeats!");
    				break;
    			}
    		}
    	}
    }

3.二叉查找树的构造（根据数组的元素创建二叉查找树）

按照二叉树插入节点的规则，依次将数组中每个元素作为节点插入到二叉树中，即可完成二叉树的构造。
例1：按照序列str={50, 66, 60, 26, 21, 30, 70, 68}建立二叉查找树
在这里插入图片描述
例2：按照序列str={50, 26, 21, 30, 66, 60, 70, 68}建立二叉查找树
在这里插入图片描述
例3：按照序列str={26, 21, 30, 50, 60, 66, 68, 70}建立二叉查找树在这里插入图片描述
由构造后的结果可以观察到，例1与例2构造出了相同的二叉排序树，而例3构造出了与前两者不同的二叉排序树。

结论：不同的关键字序列可能得到同款二叉排序树，也可能得到不同款二叉排序树

    public void createTree(int[] nums) {
    	root = new TreeNode(nums[0]); // 数组第一个为根节点
        for (int i = 1; i < nums.length; i++) { // 从第二个元素开始迭代
            TreeNode treeNode = new TreeNode();
            treeNode.val = nums[i];            
            TreeNode currentNode = root; // 要插入位置的节点，初始为root，从根节点依次寻找
            TreeNode parentNode = null; // 要插入位置的父节点
            while (currentNode != null) {
            	parentNode = currentNode;
            	if (currentNode.val > nums[i]) { // 当前节点比将要插入的值大
            		currentNode = currentNode.left; // 与根节点左子树比较
            		if (currentNode == null) { // 若左节点为空 则直接插入即可
            			parentNode.left = treeNode;
            			System.out.println(nums[i] + " has been inserted into the binary tree!");
            			break;
            		}
            	} else if (currentNode.val < nums[i]) { // 当前节点比将要插入的值小
            		currentNode = currentNode.right; // 与根节点右子树比较
            		if (currentNode == null) { // 若右节点为空 则直接插入即可
            			parentNode.right = treeNode;
            			System.out.println(nums[i] + " has been inserted into the binary tree!");
            			break;
                    }
            	} else {
            		System.out.println(nums[i]+" repeats!");
            		break;
                }
            }            
        }
    }

4.删除与val值相同的节点

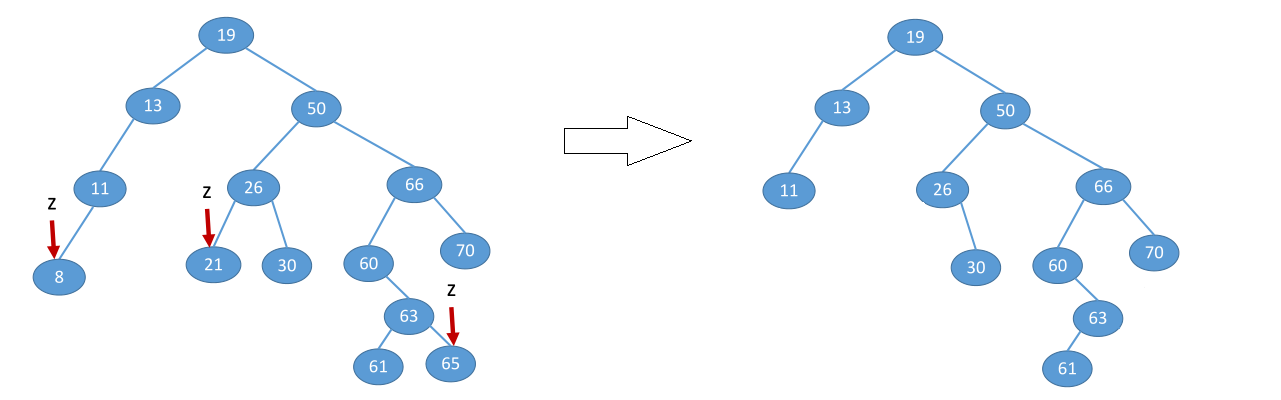
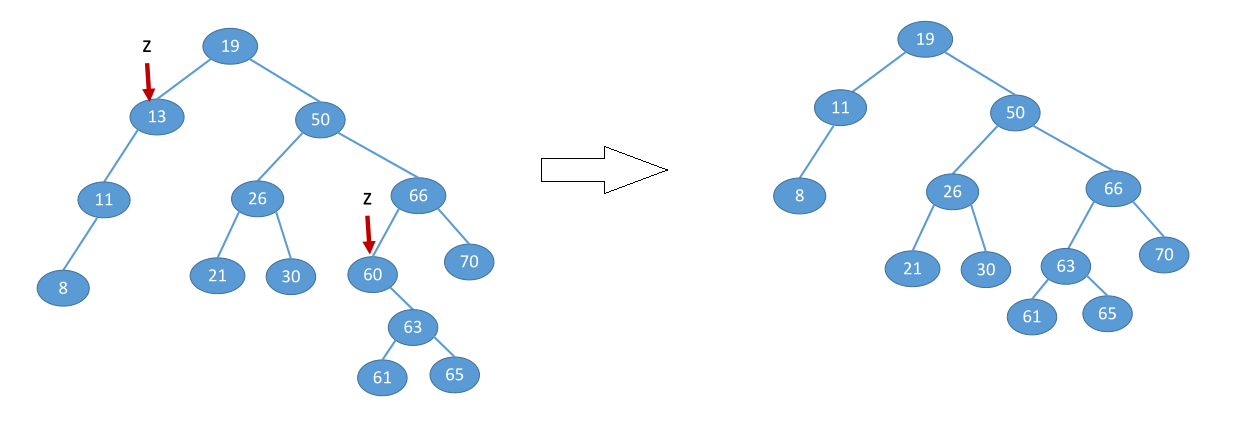
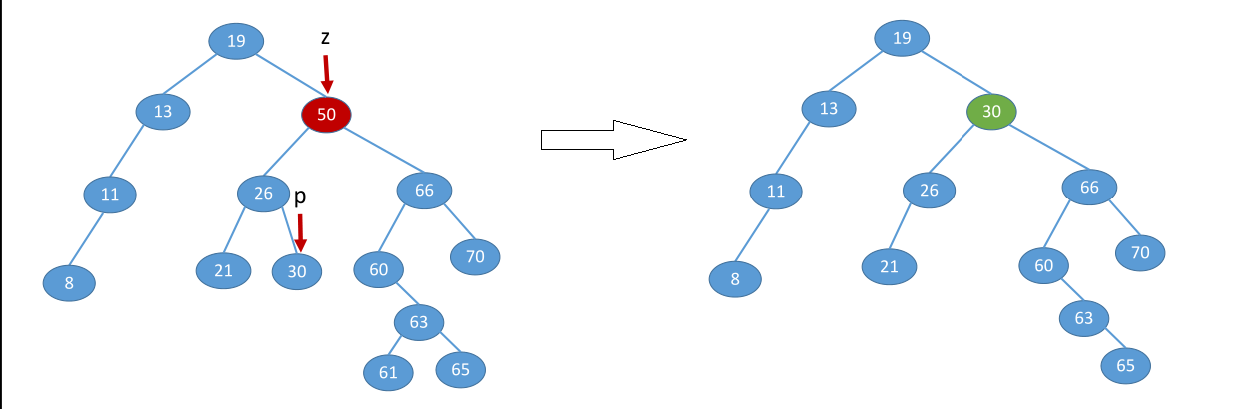
由于是二叉搜索树，删除与val值相等的“z”节点共三种情况

情况1： z节点是叶子节点，由于删去叶子结点不破坏整棵树的结构，则只需修改其双亲结点的指针即可，即直接删除currentNode节点。
在这里插入图片描述

情况2： z节点有一个叶子节点（可能是左子节点leftNode或者右子节点rightNode），此时只要令左子节点leftNode或右子节点rightNode直接成为z的双亲结点的左子树即可，作此修改也不破坏二叉查找树的特性。
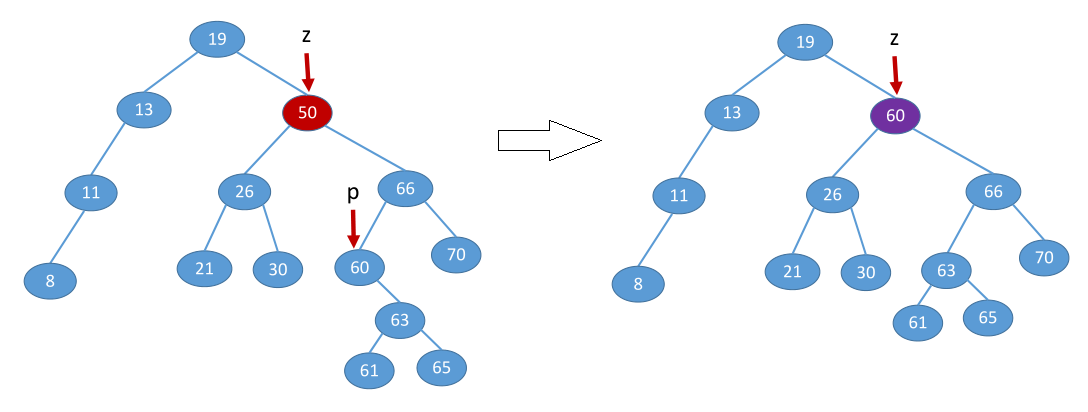
在这里插入图片描述

情况3： z节点有两个叶子节点（左子节点leftNode和右子节点rightNode），在删去z之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整。
具体方案为：则令z的直接后继（或直接前驱）节点p替代z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。

  • z的后继：z的右子树中最左下结点（该节点一定没有左子树）
  • z的前驱 ：z的左子树中最右下结点（该节点一定没有右子树）

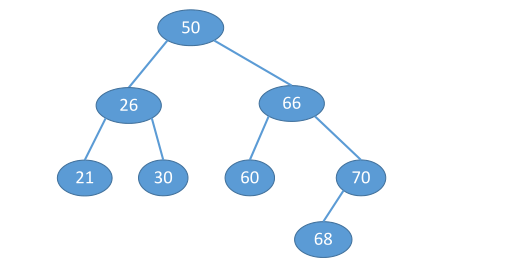
例：删除值为50的节点z。
方法一：删除直接后继
在这里插入图片描述

方法二：删除直接前驱
在这里插入图片描述

    public void remove(int val) {
    	TreeNode currentNode = root;
    	TreeNode parentNode = null; // 要插入位置的父节点
		boolean isLeftChild = false; // 判断是父节点的左子树还是右子树
		TreeNode findTreeNode = new TreeNode();
		//寻找删除的节点
    	while (currentNode != null && currentNode.val != val) {
    		parentNode = currentNode;
			if (currentNode.val > val) { // 当前节点比将要插入的值大
				currentNode = currentNode.left; // 去根节点左子树中继续寻找
				isLeftChild = true;
			} else if (currentNode.val < val) { // 当前节点比将要插入的值小
				currentNode = currentNode.right; // 去根节点右子树中继续寻找
				isLeftChild = false;
			}
    	}
    	findTreeNode = currentNode;
    	
//    	System.out.println(currentNode.val + " has been find!");
    	// 1 如果该节点是叶子节点，只用将其叶子节点删掉即可。
    	if (currentNode.left == null && currentNode.right == null) {
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = null;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = null;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = null;
    		}
    	} else if(currentNode.left != null && currentNode.right == null) {
    	// 2 该节点有一个叶子节点，叶子结点为左节点
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = currentNode.left;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = currentNode.left;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = currentNode.left;
    		}
    	} else if(currentNode.left == null && currentNode.right != null) {	
    	// 2 该节点有一个叶子节点，叶子结点为右节点
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = currentNode.right;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = currentNode.right;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = currentNode.right;
    		}
    	} else {
    	// 3 该节点有两个叶子节点
    	//删除节点用左子树中最大值结点（前驱节点）代替，或右子树最小值节点（后继节点）代替
    		// 寻找右子树最小值节点，即后继节点
    		TreeNode successorNode = currentNode; // 后继节点
    		TreeNode successorParent  = currentNode; // 后继节点的父节点
    		TreeNode rightCurrentNode  = currentNode.right; // 先进入当前节点的右子树
    		while (rightCurrentNode != null) {
    			successorParent = successorNode;
    			successorNode = rightCurrentNode;
    			rightCurrentNode = rightCurrentNode.left; // 寻找右子树的左子树（寻找最小值）
    		}
    		//successorNode的左子树成为其父节点的右子树
    		// 然后其右子树更新指向currentNode的右子树
    		if(successorNode != currentNode.right) {
    			successorParent.left = successorNode.right;
    			successorNode.right = currentNode.right;
    		}
    		
    		// 开始删除
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = successorNode;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = successorNode;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = successorNode;
    		}
    		successorNode.left = currentNode.left; // 更新左节点
    	}
    	System.out.println(findTreeNode.val + " has been removed!");
    	
    }

三、二叉搜索树操作的完整代码（包含测试）

import java.util.LinkedList;
import java.util.Queue;

public class BinarySortTree {
	
	// Definition for a binary tree node.
	public class TreeNode {
		int val;
		TreeNode left;
		TreeNode right;
		TreeNode() {}
		TreeNode(int val) {
			this.val = val;
		}
		TreeNode(int val, TreeNode left, TreeNode right) {
			this.val = val;
			this.left = left;
			this.right = right;
		}
	}
	
	
    TreeNode root; // 新建根节点
    /*
     * 根据数组的元素直接创建二叉树
     */
    public void createTree(int[] nums) {
    	root = new TreeNode(nums[0]); // 数组第一个为根节点
        for (int i = 1; i < nums.length; i++) { // 从第二个元素开始迭代
            TreeNode treeNode = new TreeNode();
            treeNode.val = nums[i];            
            TreeNode currentNode = root; // 要插入位置的节点，初始为root，从根节点依次寻找
            TreeNode parentNode = null; // 要插入位置的父节点
            while (currentNode != null) {
            	parentNode = currentNode;
            	if (currentNode.val > nums[i]) { // 当前节点比将要插入的值大
            		currentNode = currentNode.left; // 与根节点左子树比较
            		if (currentNode == null) { // 若左节点为空 则直接插入即可
            			parentNode.left = treeNode;
            			System.out.println(nums[i] + " has been inserted into the binary tree!");
            			break;
            		}
            	} else if (currentNode.val < nums[i]) { // 当前节点比将要插入的值小
            		currentNode = currentNode.right; // 与根节点右子树比较
            		if (currentNode == null) { // 若右节点为空 则直接插入即可
            			parentNode.right = treeNode;
            			System.out.println(nums[i] + " has been inserted into the binary tree!");
            			break;
                    }
            	} else {
            		System.out.println(nums[i]+" repeats!");
            		break;
                }
            }            
        }
    }
       
    /**
     * 在二叉树中插入节点
     * 要插入节点，必须先找到插入的位置。
     * 由于二叉搜索树的特殊性，待插入的节点需要从根节点开始进行比较
     * 小于根节点则与根节点左子树比较，反之则与右子树比较，直到左子树为空或右子树为空
     * 则插入到相应为空的位置
     * 在比较的过程中要注意保存父节点的信息及待插入的位置是父节点的左子树还是右子树
     * @param val
     */
    public void insert(int val) {
    	TreeNode treeNode = new TreeNode();
    	treeNode.val = val;
    	if (root == null) { // 如果根节点为空，说明是个空树
    		root = treeNode;
    		System.out.println(val + " has been inserted into the binary tree!");
    	} else {
    		TreeNode currentNode = root; // 要插入位置的节点，初始为root，从根节点依次寻找
			TreeNode parentNode = null; // 要插入位置的父节点
    		while (currentNode != null) {
    			parentNode = currentNode;
    			if (currentNode.val > val) { // 当前节点比将要插入的值大
    				currentNode = currentNode.left; // 与根节点左子树比较
    				if (currentNode == null) { // 若左节点为空 则直接插入即可
    					parentNode.left = treeNode;
    					System.out.println(val + " has been inserted into the binary tree!");
    					break;
    				}	
    			} else if (currentNode.val < val) { // 当前节点比将要插入的值小
    				currentNode = currentNode.right; // 与根节点右子树比较
    				if (currentNode == null) { // 若右节点为空 则直接插入即可
    					parentNode.right = treeNode;
    					System.out.println(val + " has been inserted into the binary tree!");
    					break;
    				}
    			} else {
    				System.out.println(val + " repeats!");
    				break;
    			}
    		}
    	}
    }
	
    // 查找与val数值相等的节点
    public void get(int val) {
    	TreeNode currentNode = root;
    	TreeNode findTreeNode = new TreeNode();
    	while (currentNode != null) {
			if (currentNode.val > val) { // 当前节点比将要插入的值大
				currentNode = currentNode.left; // 去根节点左子树中继续寻找
			} else if (currentNode.val < val) { // 当前节点比将要插入的值小
				currentNode = currentNode.right; // 去根节点右子树中继续寻找
			} else if (currentNode.val == val)  {
				findTreeNode = currentNode; //相等，则currentNode是要寻找的节点。
				System.out.println(findTreeNode.val + " has been found!");
				return;
			}
    	}
    	System.out.println("Error! " + val + " does not exist!");
    }
    
    
    /**
     * 删除与val值相同的节点
     * 删除共三种情况
     * 1 该节点是叶子节点
     * 2 该节点有一个叶子节点
     * 3 该节点有两个叶子节点
     * @param val
     */
    public void remove(int val) {
    	TreeNode currentNode = root;
    	TreeNode parentNode = null; // 要插入位置的父节点
		boolean isLeftChild = false; // 判断是父节点的左子树还是右子树
		TreeNode findTreeNode = new TreeNode();
		//寻找删除的节点
    	while (currentNode != null && currentNode.val != val) {
    		parentNode = currentNode;
			if (currentNode.val > val) { // 当前节点比将要插入的值大
				currentNode = currentNode.left; // 去根节点左子树中继续寻找
				isLeftChild = true;
			} else if (currentNode.val < val) { // 当前节点比将要插入的值小
				currentNode = currentNode.right; // 去根节点右子树中继续寻找
				isLeftChild = false;
			}
    	}
    	findTreeNode = currentNode;
    	
//    	System.out.println(currentNode.val + " has been find!");
    	// 1 如果该节点是叶子节点，只用将其叶子节点删掉即可。
    	if (currentNode.left == null && currentNode.right == null) {
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = null;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = null;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = null;
    		}
    	} else if(currentNode.left != null && currentNode.right == null) {
    	// 2 该节点有一个叶子节点，叶子结点为左节点
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = currentNode.left;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = currentNode.left;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = currentNode.left;
    		}
    	} else if(currentNode.left == null && currentNode.right != null) {	
    	// 2 该节点有一个叶子节点，叶子结点为右节点
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = currentNode.right;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = currentNode.right;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = currentNode.right;
    		}
    	} else {
    	// 3 该节点有两个叶子节点
    	//删除节点用左子树中最大值结点（前驱节点）代替，或右子树最小值节点（后继节点）代替
    		// 寻找右子树最小值节点，即后继节点
    		TreeNode successorNode = currentNode; // 后继节点
    		TreeNode successorParent  = currentNode; // 后继节点的父节点
    		TreeNode rightCurrentNode  = currentNode.right; // 先进入当前节点的右子树
    		while (rightCurrentNode != null) {
    			successorParent = successorNode;
    			successorNode = rightCurrentNode;
    			rightCurrentNode = rightCurrentNode.left; // 寻找右子树的左子树（寻找最小值）
    		}
    		//successorNode的左子树成为其父节点的右子树
    		// 然后其右子树更新指向currentNode的右子树
    		if(successorNode != currentNode.right) {
    			successorParent.left = successorNode.right;
    			successorNode.right = currentNode.right;
    		}
    		
    		// 开始删除
    		if (currentNode == root) { // 是根节点，即该树只有一个节点
    			currentNode = successorNode;
    		} else if (isLeftChild) { // 是其父节点的左子树节点
    			parentNode.left = successorNode;
    		} else if (!isLeftChild) { // 是其父节点的右子树节点
    			parentNode.right = successorNode;
    		}
    		successorNode.left = currentNode.left; // 更新左节点
    	}
    	System.out.println(findTreeNode.val + " has been removed!");
    	
    }
    
	// 树的先序遍历
	public void preOrderTraversal (TreeNode root) {
		if (root == null) {
			return;
		}
		System.out.print(root.val + " "); //先输出当前节点（初始的时候是root节点）
		preOrderTraversal(root.left); // 如果左子节点不为空，则递归继续前序遍历
		preOrderTraversal(root.right); // 如果右子节点不为空，则递归继续前序遍历
	}
	
	// 树的中序遍历
	public void inOrderTraversa (TreeNode root) {
		if (root == null) {
			return;
		}
		inOrderTraversa(root.left); // 如果当前节点的左子节点不为空，则递归中序遍历
		System.out.print(root.val + " "); // 输出当前节点
		inOrderTraversa(root.right); // 如果当前的右子节点不为空，则递归中序遍历		
	}
	
	// 树的后序遍历
	public void postOrderTraversal (TreeNode root) {
		if (root == null) {
			return;
		}
		postOrderTraversal(root.left); // 如果当前节点的左子节点不为空，则递归后序遍历
		postOrderTraversal(root.right); // 如果当前节点的右子节点不为空，则递归后序遍历
		System.out.print(root.val + " "); // 输出当前节点		
	}

    // 广度优先遍历，即树的层次遍历，借用队列实现
    public void levelOrderTraversal(TreeNode root) {
    	if(root == null) {
    		return;
    	}    	
    	Queue<TreeNode> queue = new LinkedList<TreeNode>(); // 存放每层操作的根节点
        queue.offer(root);        
        while (!queue.isEmpty()) {
            int queueSize = queue.size();
            for (int i = 0; i < queueSize; i++) { // 用for循换可以隔离开每一层的遍历
            	TreeNode rootNode = queue.poll(); // 开始操作后将其从队列移除
            	System.out.print(rootNode.val + " ");
                if (rootNode.left != null) {
    	            TreeNode leftNode = rootNode.left; // 左节点存入队列，下一层遍历它就成了新根节点	            
    	            queue.offer(leftNode);
                }
                if (rootNode.right != null) {
                	TreeNode rightNode = rootNode.right; // 右节点存入队列，下一层遍历它就成了新根节点
                	queue.offer(rightNode);
                }
            }
        }
    }
    
    public static void main(String[] args) {
		BinarySortTree binarySortTree = new BinarySortTree();
		
		binarySortTree.createTree(new int[]{7, 1, 5, 9, 3, 0, 2, 6, 8});

		binarySortTree.insert(4);
		
		binarySortTree.get(5);
		
		System.out.print("先序遍历：");
		binarySortTree.preOrderTraversal(binarySortTree.root);
		System.out.println();
		System.out.print("中序遍历：");
		binarySortTree.inOrderTraversa(binarySortTree.root);
		System.out.println();
		System.out.print("后序遍历：");
		binarySortTree.postOrderTraversal(binarySortTree.root);
		System.out.println();
		System.out.print("层次遍历：");
		binarySortTree.levelOrderTraversal(binarySortTree.root);
		System.out.println();
		
		binarySortTree.remove(3);
		
		System.out.print("先序遍历：");
		binarySortTree.preOrderTraversal(binarySortTree.root);
		System.out.println();
		System.out.print("中序遍历：");
		binarySortTree.inOrderTraversa(binarySortTree.root);
		System.out.println();
		System.out.print("后序遍历：");
		binarySortTree.postOrderTraversal(binarySortTree.root);
		System.out.println();
		System.out.print("层次遍历：");
		binarySortTree.levelOrderTraversal(binarySortTree.root);
		System.out.println();
	}
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
Redis实战篇--商户查询缓存
关于getContentView
富文本编辑器：图片和文件可上传至服务器
Vue中实现路由跳转传参的4种方式
【总线】AXI第九课时：介绍AXI响应信号 (Response Signaling)：RRESP和 BRESP
ubuntu14.04手动更换内核方法
带你了解ChatGPT
十一 Java序列化
YOLO系列详解：YOLOv1、YOLOv2、YOLOv3、YOLOv4、YOLOv5、YOLOv6、YOLOv7
[转载]petshop解析
;