快速排序采用“分而治之、各个击破”的观念。

快速排序是二叉查找树（二叉搜索树）的一个空间最优化版本。不是循序地把数据项插入到一个明确的树中，而是由快速排序组织这些数据项到一个由递归调用所隐含的树中。这两个算法完全地产生相同的比较次数，但是顺序不同。对于排序算法的稳定性指标，原地分区版本的快速排序算法是不稳定的。其他变种是可以通过牺牲性能和空间来维护稳定性的。

快速排序的最直接竞争者是堆排序（Heapsort）。堆排序通常比快速排序稍微慢，但是最坏情况的运行时间总是。快速排序是经常比较快，除了introsort变化版本外，仍然有最坏情况性能的机会。如果事先知道堆排序将会是需要使用的，那么直接地使用堆排序比等待introsort再切换到它还要快。堆排序也拥有重要的特点，仅使用固定额外的空间（堆排序是原地排序），而即使是最佳的快速排序变化版本也需要的空间。然而，堆排序需要有效率的随机存取才能变成可行。

快速排序也与归并排序（Mergesort）竞争，这是另外一种递归排序算法，但有坏情况运行时间的优势。不像快速排序或堆排序，归并排序是一个稳定排序，且可以轻易地被采用在链表（linked list）和存储在慢速访问媒体上像是磁盘存储或网络连接存储的非常巨大数列。尽管快速排序可以被重新改写使用在链串列上，但是它通常会因为无法随机存取而导致差的基准选择。归并排序的主要缺点，是在最佳情况下需要额外的空间。

快速排序的步骤如下：(注意：这里第一步的基准我们不按照常规取最左端为基准而是随机选择一个数据作为基准)

1.从数列中挑出一个元素，称为“基准”（pivot），

2.重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

3.递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

4.递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

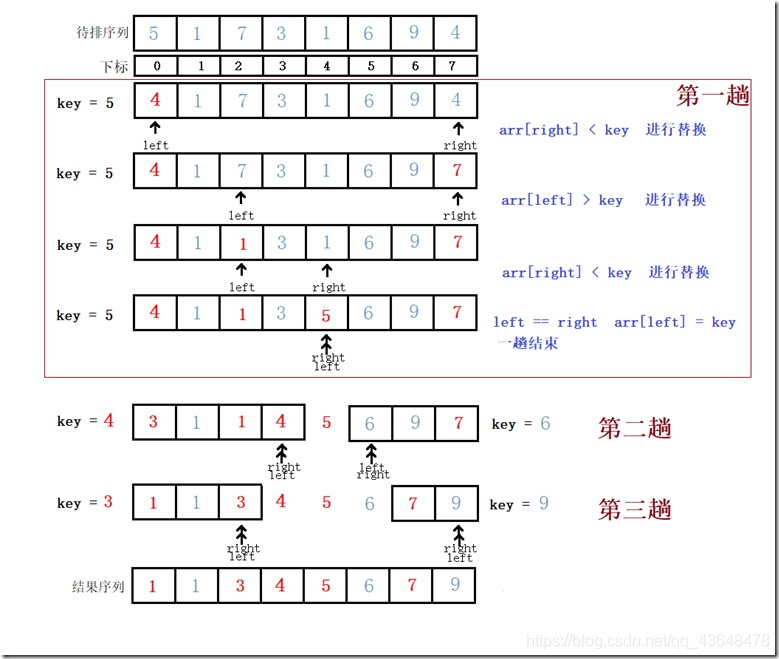
这里给出一各排序的图解过程，掌握这个图解快速排序的核心你就掌握了

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
int portition(int a[],int left,int right) {
	int temp=a[left];
	while(left<right) {
		while(left<right&&a[right]>=temp)right--;
		a[left]=a[right];
		while(left<right&&a[left]<=temp)left++;
		a[right]=a[left];
	}
	a[left]=temp;
	return left;
}
void quicksort(int R[],int left,int right) {
	if(left<right) {
		int i;
		int pivot=rand()%(right-left+1)+left; //rand()%(right-left+1)+left从 left-righ中随机选中一个下标
		int temp=R[pivot];//把随机选中的数组下标的数据与R[left]交换数据
		R[pivot]=R[left];
		R[left]=temp;
		i=portition(R,left,right);
		quicksort(R,left,i-1);
		quicksort(R,i+1,right);
	}
}
int main() {
	int n,j,i;
	printf("请输入要排序的数据总个数:");
	scanf("%d",&n);
	int *a=(int *)malloc(sizeof(int)*n);
	printf("请输入%d个数据:",n);
	for(i=0; i<n; i++)
		scanf("%d",a+i);
	quicksort(a,0,n-1);
	printf("快速排序后:");
	for(i=0; i<n; i++)
		printf("%d ",*(a+i));
	return 0;
}