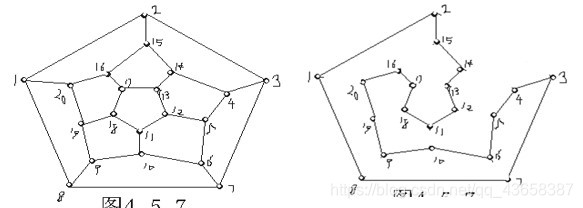
哈密尔顿图(Hamilton Graph)
对于图每个顶点只访问一次，并且返回起点
Example：

思路：

Reference：https://www.geeksforgeeks.org/hamiltonian-cycle-backtracking-6/

1. 首先创建一个空的path，并且将0这个点(随机选择的起点)加入其中
2. 从1开始添加后续顶点，在添加后续顶点之前首先要检查这些顶点是不是与之前添加的顶点相邻并且没有添加过
3. 如果找到了这样的点的话，就将它添加到path中去，接着判断下一个位置的点
4. 在此之前先要判断现在path中点的数量是不是已经是全部点的个数了，如果是的话要判断头结点和尾节点是不是存在边，如果存在的话，就输出path
5. 如果不存在，就要将刚才加入的点给弹出，继续加入下一个有效点测试

class Graph:
    def __init__(self, vertices):
        self.graph = [[0 for col in range(vertices)] \
                      for row in range(vertices)]
        self.V = vertices

    # 检查当前结点是否为之前刚加入节点的邻接点，并且没有收录到path中
    def isSafe(self, v, pos, path):
        # 检查当前节点和path中最后一个节点是否邻接
        if self.graph[path[pos - 1]][v] == 0:
            return False
        # 如果当前节点不在path中
        if v in path:
            return False
        return True

    def hamCycleUtil(self, path, pos):
        if pos == self.V: # 递归终止条件：当检查完所有的节点时
            if self.graph[path[pos - 1]][path[0]] == 1: # 最后一个节点必须和起点邻接才是Hamilton graph
                return True
            else:
                return False
        for v in range(1, self.V): 
            """
            枚举图中的节点检查是否为当前节点pos邻接
            因为哈密尔顿图需要走过所有节点，所以直到最后才检查是否与起点邻接
            0为起点，所以先跳过0
            """
            if self.isSafe(v, pos, path) == True:
                path[pos] = v # 收录到path中
                if self.hamCycleUtil(path, pos + 1) == True:
                    return True
                path[pos] = -1 # 没有Hamilton回路就重置

        return False

    def hamCycle(self):
        path = [-1] * self.V
        path[0] = 0 # 以0为起点
        if self.hamCycleUtil(path, 1) == False: # 从位置1开始
            print("Solution does not exist")
            return False

        self.printSolution(path)
        return True

    def printSolution(self, path):
        print("Solution Exists: Following is one Hamiltonian Cycle")
        for vertex in path:
            print(vertex, end=' ')
        print(path[0])

        
'''
the following graph is a hamilton graph
      (0)--(1)--(2) 
       |   / \   | 
       |  /   \  | 
       | /     \ | 
      (3)-------(4)    
'''
g1 = Graph(5)
g1.graph = [[0, 1, 0, 1, 0],
            [1, 0, 1, 1, 1],
            [0, 1, 0, 0, 1],
            [1, 1, 0, 0, 1],
            [0, 1, 1, 1, 0],]
g1.hamCycle() 
# Solution Exists: Following is one Hamiltonian Cycle
# 0 1 2 4 3 0