根据MATLAB中文论坛中内容，基于MATLAB可轻松实现多维正态和T-Copula。

在实际运用Copula函数时，总想运用到更高维，但到底要如何实现呢？此篇文章主要想尝试一下用MATLAB现成的函数实现多元正态Copula。感受一下多维Copula是个什么感觉。

1 与正态Copula有关的MATLAB函数

1.1 copulafit函数

copulafit函数用来根据样本观测数据估计Copula函数中的未知参数。
与正态Copula有关的调用格式如下：

RHOHAT = copulafit('Gaussian', U)

输入变量U是由边缘分布函数值构成的n×p的矩阵，表示p个变量，n组观测，其元素取值范围为[0,1]。
输出变量RHOHAT为p×p的矩阵。
估计正态Copula中的线性相关参数ρ，估计ρ的估计值矩阵RHOHAT。

1.2 copulacdf函数

copulacdf函数用来计算Copula函数分布函数值。
与正态Copula有关的调用格式如下：

Y = copulacdf('Gaussian', U,rho)

输入变量:

• U是由边缘分布函数值构成的n×p的矩阵，表示p个变量，n组观测，其元素取值范围为[0,1]。
• rho为p×p的线性相关系数矩阵，即copulafit计算得到的RHOHAT。
  计算线性相关参数为rho的正态Copula的密度函数值Y。

1.3 copulapdf函数

copulapdf函数用来计算Copula函数密度函数值。
与正态Copula有关的调用格式如下：

Y = copulapdf('Gaussian', U,rho)

输入变量:

• U是由边缘分布函数值构成的n×p的矩阵，表示p个变量，n组观测，其元素取值范围为[0,1]。
• rho为p×p的线性相关系数矩阵，即copulafit计算得到的RHOHAT。
  计算线性相关参数为rho的正态Copula的分布函数值Y。

2 具体案例

随机生成3个变量，并运用上述代码进行Copula函数拟合。代码如下：

clc
close all
clear
%% 以3维为例
N = 1000;
X = rand(N,1);
Y = rand(N,1);
Z = rand(N,1);

%% 1)进行边缘分布的拟合检验，选取最优边缘分布拟合函数
% 变量X
[fx,xc] = ecdf(X);
XpdNormal= fitdist(X ,'normal');             % 进行正态分布拟合
[XhNormal,XpNormal ,XksstatNormal ,XcvNormal ]= kstest(X , [ X , normcdf(X,XpdNormal.mu , XpdNormal.sigma )]);
Xfit = normpdf(xc,XpdNormal.mu , XpdNormal.sigma );

Ucdf = ksdensity( X , X , 'function' ,'cdf');
% 选择正态分布拟合 cdf为分布函数======================================
U = gevcdf(X,XpdNormal.mu , XpdNormal.sigma);  
f1 = gevcdf(linspace(min(X),max(X) ,50) ,XpdNormal.mu , XpdNormal.sigma );

% 变量Y
[fy,yc] = ecdf(Y);
YpdNormal= fitdist(Y ,'normal');             % 进行正态分布拟合
[YhNormal,YpNormal ,YksstatNormal ,YcvNormal ]= kstest(Y , [ Y , normcdf(Y,YpdNormal.mu , YpdNormal.sigma )]);
Yfit = normpdf(yc,YpdNormal.mu , YpdNormal.sigma );

Vcdf = ksdensity( Y , Y , 'function' ,'cdf');
% 选择正态分布拟合 cdf为分布函数======================================
V = gevcdf(Y,YpdNormal.mu , YpdNormal.sigma);  
f2 = gevcdf(linspace(min(Y),max(Y) ,50) ,YpdNormal.mu , YpdNormal.sigma );

% 变量Z
[fz,zc] = ecdf(Z);
ZpdNormal= fitdist(Z ,'normal');             % 进行正态分布拟合
[ZhNormal,ZpNormal ,ZksstatNormal ,ZcvNormal ]= kstest(Z , [ Z , normcdf(Z,ZpdNormal.mu , ZpdNormal.sigma )]);
Zfit = normpdf(zc,ZpdNormal.mu , ZpdNormal.sigma );

Wcdf = ksdensity( Z , Z , 'function' ,'cdf');
% 选择正态分布拟合 cdf为分布函数======================================
W = gevcdf(Z,ZpdNormal.mu , ZpdNormal.sigma);  
f3 = gevcdf(linspace(min(Z),max(Z) ,50) ,ZpdNormal.mu , ZpdNormal.sigma );

figure(1);

subplot(2,2,1)
ecdfhist(fx,xc,30);
h = findobj(gca,'Type','patch');
h.FaceColor = [.9 .9 .9];
hold on
xlabel("X");
ylabel("f(x)");
x_values = linspace(min(X),max(X));
h(1)= plot(x_values,normpdf( x_values ,XpdNormal.mu , XpdNormal.sigma ),'g-','linewidth',1.5);
hl = legend(h([1]),"Normal distribution");
set(hl,'Box','off','Location','none','position',[0.62 0.7 0.1 0.1],'FontSize',14);
text( 'string',"(a) X", 'Units','normalized','position',[0.02,0.9],  'FontSize',14,'FontWeight','Bold','FontName','Times New Roman');   
set(gca,'ylim',[0 1.6]);  
set(gca,'FontSize',12,'Fontname', 'Times New Roman');

subplot(2,2,2)
ecdfhist(fy,yc,30);
h = findobj(gca,'Type','patch');
h.FaceColor = [.9 .9 .9];
hold on
xlabel("Y");
ylabel("f(y)");
y_values = linspace(min(Y),max(Y));
h(1)= plot(y_values,normpdf( y_values ,YpdNormal.mu , YpdNormal.sigma ),'g-','linewidth',1.5);
% hl = legend(h([1]),"Normal distribution");
set(hl,'Box','off','Location','none','position',[0.62 0.7 0.1 0.1],'FontSize',14);
text( 'string',"(b) Y", 'Units','normalized','position',[0.02,0.9],  'FontSize',14,'FontWeight','Bold','FontName','Times New Roman');   
set(gca,'ylim',[0 1.6]);  
set(gca,'FontSize',12,'Fontname', 'Times New Roman');

subplot(2,2,3)
ecdfhist(fz,zc,30);
h = findobj(gca,'Type','patch');
h.FaceColor = [.9 .9 .9];
hold on
xlabel("Z");
ylabel("f(z)");
z_values = linspace(min(Z),max(Z));
h(1)= plot(z_values,normpdf( z_values ,ZpdNormal.mu , ZpdNormal.sigma ),'g-','linewidth',1.5);
% hl = legend(h([1]),"Normal distribution");
set(hl,'Box','off','Location','none','position',[0.62 0.7 0.1 0.1],'FontSize',14);
text( 'string',"(c) Z", 'Units','normalized','position',[0.02,0.9],  'FontSize',14,'FontWeight','Bold','FontName','Times New Roman');   
set(gca,'zlim',[0 1.6]);  
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
%% 2) Copula函数参数估计:计算Copula函数的参数
% 联合分布理论值
% ------------------------------------------------------------------------------------------------------------
RhoHat = copulafit('Gaussian', [ U(:) , V(:) ,W(:) ] );
UVWNormal = copulacdf('Gaussian',  [ U(:) , V(:) ,W(:) ] ,RhoHat );

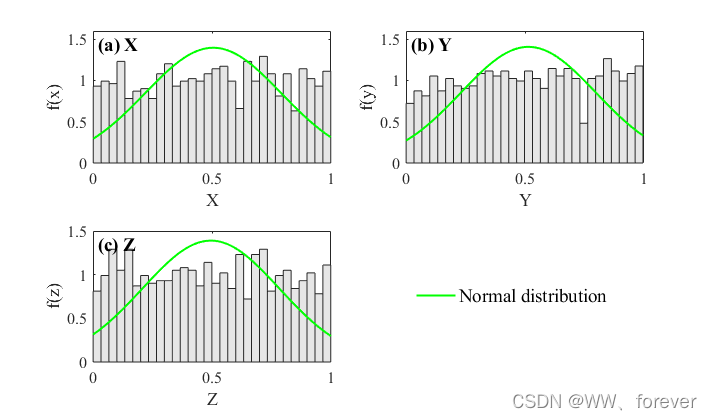
3个变量的密度函数拟合图（忽略拟合的效果并不好，只是试一下罢了）

可以得到三维正态Copula的密度函数值和分布函数值，所以然后呢？

3 思考

计算得到多元Copula分布后，能如何对结果进行分析呢？
目前就我看到的，可能是计算组合重现期，但如此提取的信息未免太少了吧。

3.1 结果展示

3.1.1三维组合重现期

参考

1.书籍-《MATLAB统计分析与应用：40个案例分析》
2.博士论文-《基于Palmer旱度模式的四湖流域旱涝急转特征分析》