本文主要介绍如何利用MATLAB解特征方程,并将特征根的分布画在坐标轴上,便于分析系统的稳定性
我们知道,一旦求出系统的闭环特征根就很容易判定系统的稳定性,但是对于高阶系统,闭环特征根求起来是很困难的,但是利用MATLAB这一强大的数学工具,求起来就很方便,也很简单了,比如求解以下特征方程的特征根:
s 6 + 3 s 5 + 16 s 4 + 2 s 3 − 4 s 2 − 25 s − 60 = 0 s^6+3s^5+16s^4+2s^3-4s^2-25s-60= 0 s6+3s5+16s4+2s3−4s2−25s−60=0
1、把特征方程中的系数按照阶次从高到低放到一个向量里面去,若有缺项,该项系数应该补零,我们以上面的式子为例:
p=[ 1 3 16 2 -4 -25 -60 ];
2、利用roots函数求解,roots函数可用于求解多项式的根,在完成上一步的情况下,只需要调用roots(p)就可以求出多项式的根。
r=roots(p)
结果如下:
r =
-1.4204 + 3.6565i
-1.4204 - 3.6565i
1.4475 + 0.0000i
-0.1563 + 1.4343i
-0.1563 - 1.4343i
-1.2941 + 0.0000i
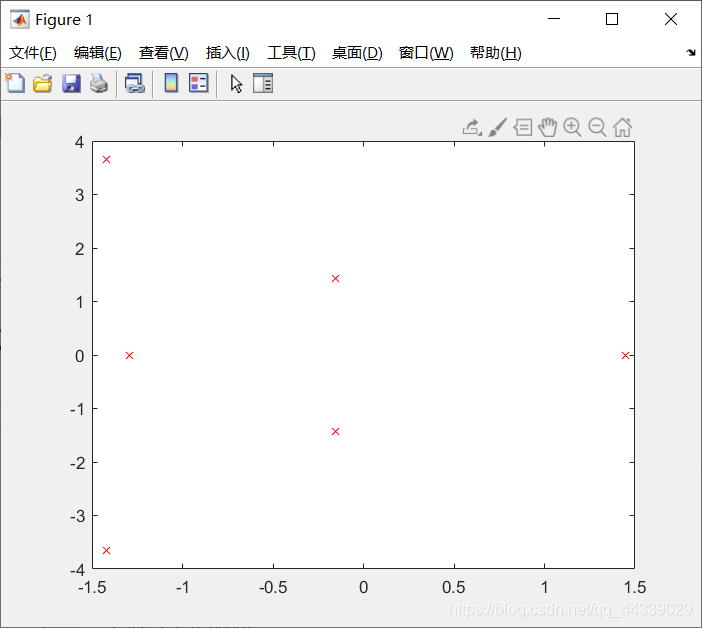
3、为了更加直观的观察根的分布我们把它画在坐标轴中,调用real()函数可以获取复数的实部,调用imag()函数可以获取复数的虚部,再利用plot()以点的形式画出来就可以了,用×来标注
h=plot(real(r),imag(r),'rX');
图像如下:
4、为了更好地观察,我们对其进行放大,再加上网格线,用set()函数设置线宽linewidth为5,设置标记符号(此处为×)的大小markersize为15,利用set(gca)可以调整图形的刻度大小,语句grid on可以在画图的时候添加网格线,此部分代码如下:
set(h,'linewidth',5,'markersize',15);
set(gca,'fontsize',15);
grid on
5、如果需要的话,可以画出实轴和虚轴,代码如下(范围自主调整):
plot([0 0],[-5 5])
plot([-2 2],[0 0])
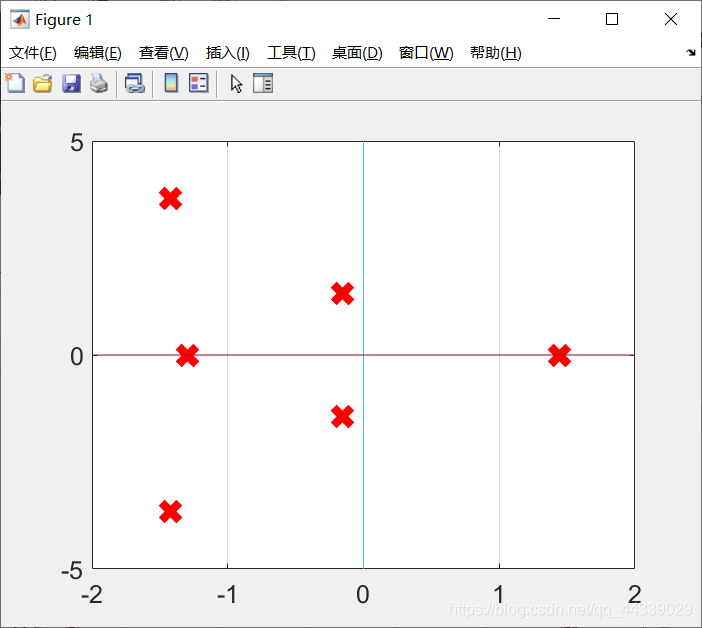
6、完整的代码和图像如下:
p=[ 1 3 16 2 -4 -25 -60 ];
r=roots(p);
h=plot(real(r),imag(r),'rX');
set(h,'linewidth',5,'markersize',15);
set(gca,'fontsize',15);
hold on
plot([0 0],[-5 5])
plot([-2 2],[0 0])
grid on
(点击图上的点可以查看坐标值,对应特征根的实部和虚部,如下)