本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
本篇文章主要介绍使用使用序列无约束优化处理约束优化的3种方法:罚函数法(Penalty Method)、障碍函数法(Barrier Method)、拉格朗日松弛法(Lagrangian Relaxation)。
二十一、罚函数法(Penalty Method)
1、将等式约束转换为二次惩罚项
罚函数法即适应于不等式约束,又适应于等式约束。对于等式约束,我们可以定义一个二次罚函数(L2-Penalty ),假设目标函数与等式约束如下所示:
min x f ( x ) s . t . c i ( x ) = 0 , i ∈ E \begin{array}{cc}\min_{x} & f(x)\\ \mathrm{s.t.} & c_{i}(x)=0,\quad i\in\mathcal{E}\end{array} minxs.t.f(x)ci(x)=0,i∈E
我们可以将等式约束构造成一个惩罚项,然后添加到目标函数中,来将约束优化转换为带惩罚项的无约束优化,如下式所示,使用无约束优化的方法进行求解
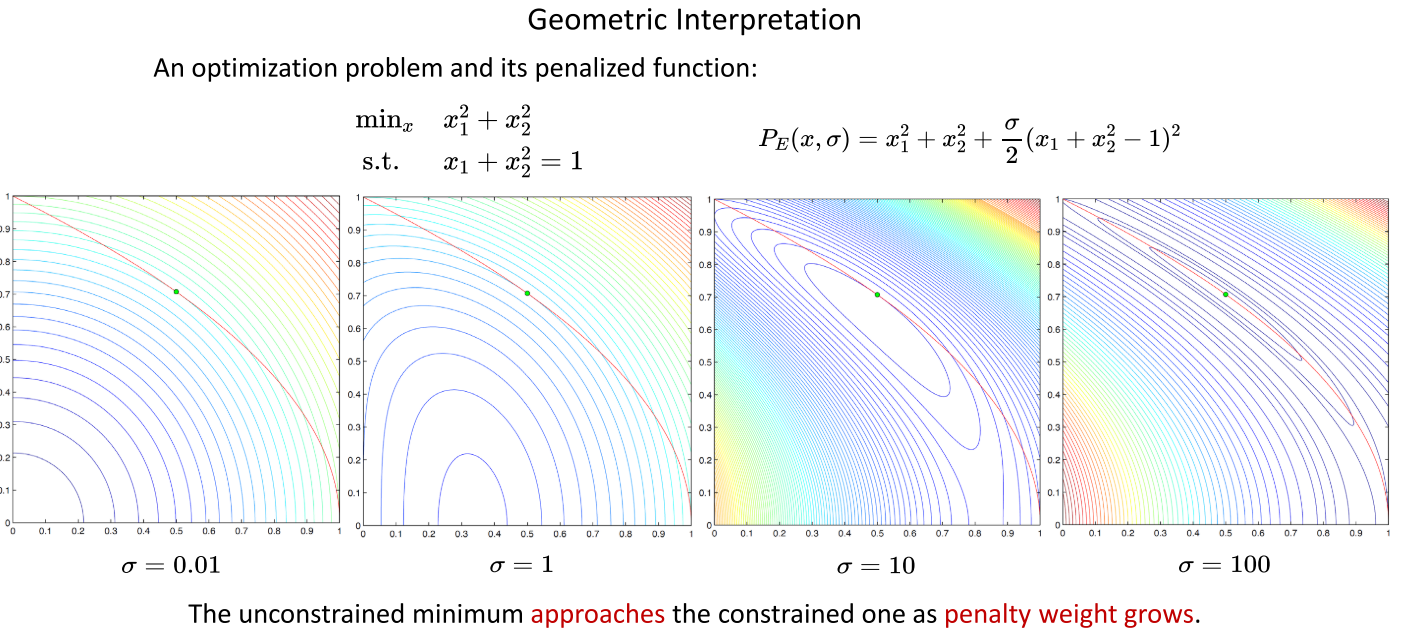
P E ( x , σ ) = f ( x ) + 1 2 σ ∑ i ∈ E c i 2 ( x ) P_E(x,\sigma)=f(x)+\color{red}{\frac12}\sigma\sum_{i\in\mathcal{E}}c_i^2(x) PE(x,σ)=f(x)+21σi∈E∑ci2(x)
上式中的 σ \sigma σ是惩罚权重,对于不满足等式约束的解,越不满足, c i ( x ) c_i(x) ci(x)偏离0越大时, c i 2 ( x ) c_i^2(x) ci2(x)也就越大,惩罚项也就越大,当 σ \sigma σ值较大时,相比于满足 c i ( x ) = 0 c_i(x)=0 ci(x)=0的解,不满足的解就会有一个较大的惩罚项,使用无约束优化算法可以得到一个近似满足等式约束的局部极小值,其精度取决于 σ \sigma σ的大小。当 σ \sigma σ趋于无穷大时,其极限收敛于原约束问题的最优解。
在下图中的例子中,当 σ \sigma σ取100时,带惩罚项的无约束目标函数的最优解几乎等价于原有带等式约束的目标函数的最优解。
2、将不等式约束转换为二次惩罚项
min f ( x ) s . t . c i ( x ) ⩽ 0 , i ∈ I \begin{aligned}\min&\quad f(x)\\\mathrm{s.t.}&\quad c_i(x)\leqslant0,\quad i\in\mathcal{I}\end{aligned} mins.t.f(x)ci(x)⩽0,i∈I
对于不等式约束,同样可以将其转换为二次惩罚项,例如对于 c i ( x ) ⩽ 0 c_i(x)\leqslant0 ci(x)⩽0这样的不等式约束,当 c i ( x ) c_i(x) ci(x)小于等于0时,满足约束,惩罚项为0,当 c i ( x ) c_i(x) ci(x)大于0时,比0大的越多,惩罚项就应该越大,所以可以借助max( c i ( x ) c_i(x) ci(x),0)函数来构造惩罚项,如下所示:
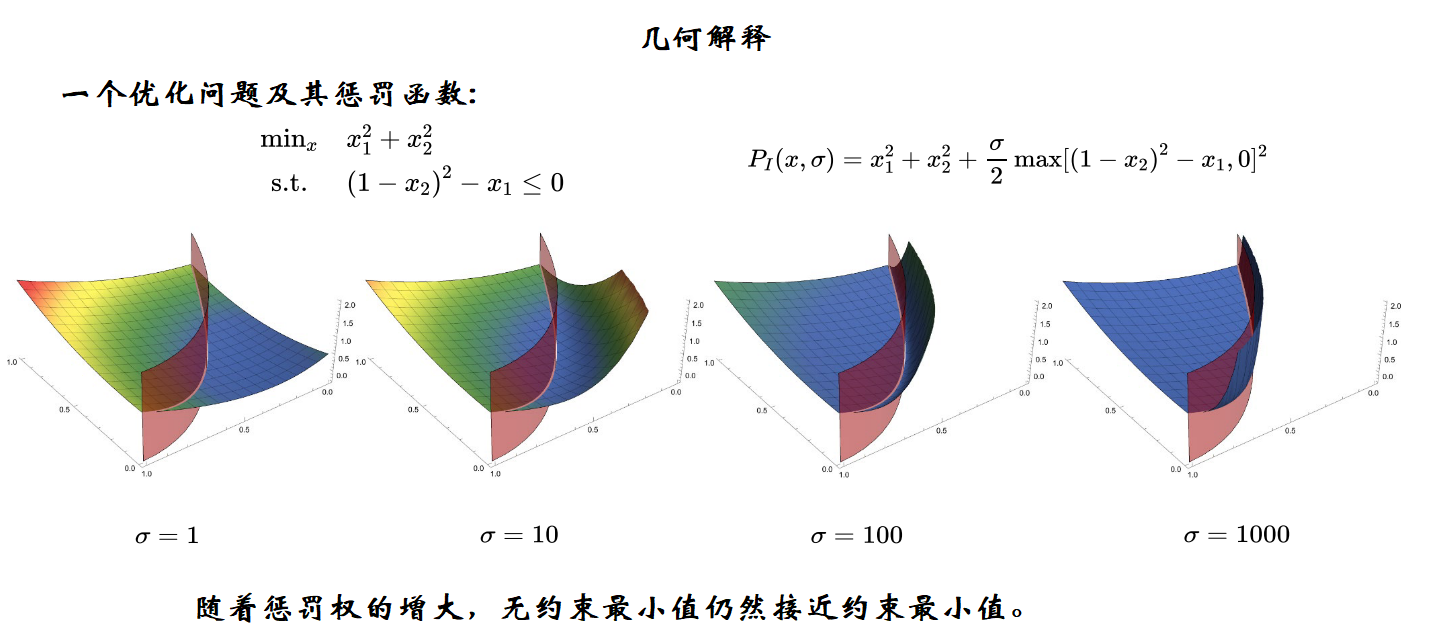
P I ( x , σ ) = f ( x ) + 1 2 σ ∑ i ∈ I max [ c i ( x ) , 0 ] 2 P_I(x,\sigma)=f(x)+\color{red}{\frac12}\sigma\sum_{i\in\mathcal{I}}\max[c_i(x),0]^2 PI(x,σ)=f(x)+21σi∈I∑max[ci(x),0]2
需要注意的是上式中的二次惩罚项,其一阶导是连续的,但二阶导是不连续的,所有可以用基于梯度的无约束优化方法,或者带cautious update条件的L-BFGS无优化方法进行优化求解。
其精度同样受 σ \sigma σ的影响。当 σ \sigma σ趋于无穷大时,其极限收敛于原约束问题的最优解。
在下图中的例子中,灰红色曲面的左侧是不等式约束的可行域,随着 σ \sigma σ的增大,可以看出该灰红色曲面右侧的函数值在快速变大,当 σ \sigma σ取1000时,该灰红色曲面右侧的函数值急剧变大,带惩罚项的无约束目标函数的最优解几乎等价于原有带不等式约束的目标函数的最优解。
所以对于带约束的优化问题,当 c i ( x ) c_i(x) ci(x)有物理意义,且精度在0.01或0.001时是可接受的,而不是很高的 1 0 − 5 10^{-5} 10−5这种高精度的时候,可以采用罚函数法将其转换为无约束问题就行求解。
3、将等式约束或不等式约束转换为一次惩罚项
有些时候,我们可以不把等式约束或不等式约束转换为二次惩罚项,而是转换为更简单的一次惩罚项,如下式所示
min f ( x ) s . t . c i ( x ) = 0 , i ∈ E c j ( x ) ⩽ 0 , j ∈ I \begin{aligned}\min&\quad f(x)\\\mathrm{s.t.}&\quad c_i(x)=0,\quad i\in\mathcal{E}\\&\quad c_j(x)\leqslant0,\quad j\in\mathcal{I}\end{aligned} mins.t.f(x)ci(x)=0,i∈Ecj(x)⩽0,j∈I
转换为下式:
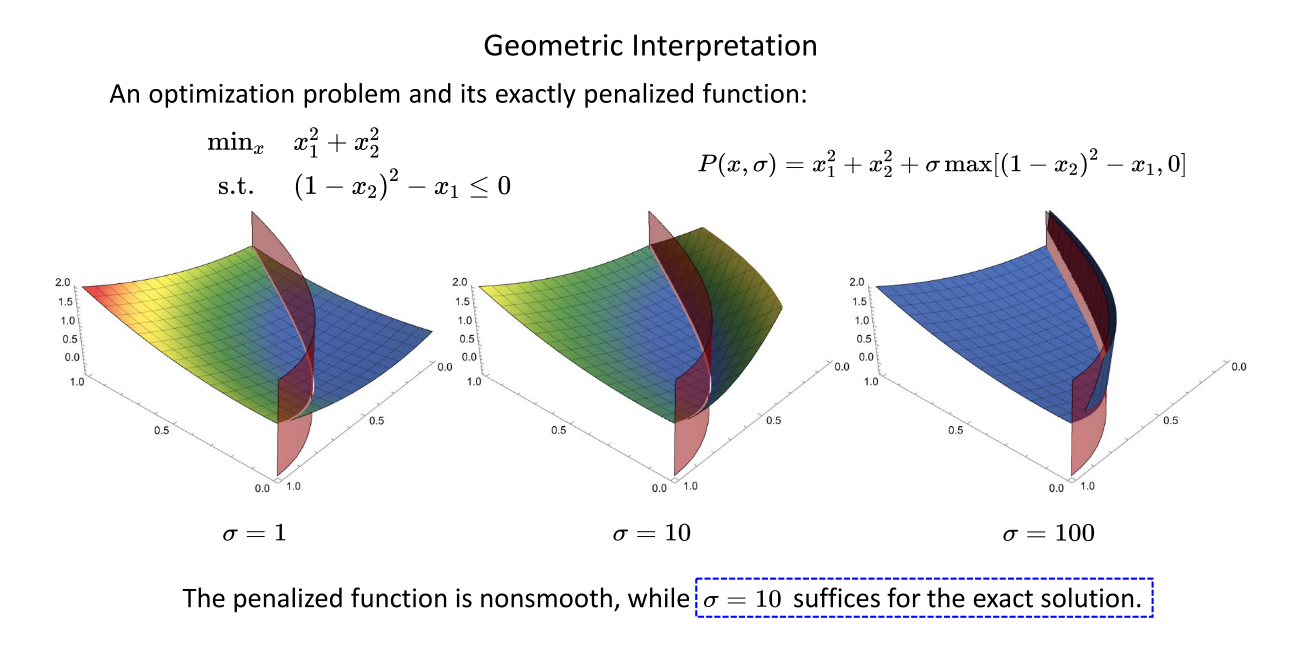
P ( x , σ ) = f ( x ) + σ ∑ i ∈ E ∣ c i ( x ) ∣ + σ ∑ j ∈ I max [ c j ( x ) , 0 ] P(x,\sigma)=f(x)+\color{red}{\sigma\sum_{i\in\mathcal{E}}|c_i(x)|+\sigma\sum_{j\in\mathcal{I}}\max[c_j(x),0]} P(x,σ)=f(x)+σi∈E∑∣ci(x)∣+σj∈I∑max[cj(x),0]
红色部分为L1罚函数,值得注意的是其导数是不连续的,在某个点处导数不存在。但也有一些优点,当 σ \sigma σ足够大的时候(有限的),不需要趋于无穷,比如 σ > 10000 \sigma>10000 σ>10000时,可以使得转换后的无约束的目标函数的最优值,跟原有的带约束的目标函数的最优值精确的相等,不是收敛意义的相等而是精确的相等。所有L1惩罚项具有精确性。
在下图所示的例子中,当 σ \sigma σ取100时,转换后的无约束目标函数最优值与转换前的带约束目标函数的最优值就可以相等
二十二、障碍函数法(Barrier Method)
障碍函数法一般只考虑不等式约束,对于下式所示的带不等式约束的目标函数的优化问题
min f ( x ) s . t . c i ( x ) ⩽ 0 , i ∈ I \begin{aligned}\min&\quad f(x)\\\mathrm{s.t.}&\quad c_i(x)\leqslant0,\quad i\in\mathcal{I}\end{aligned} mins.t.f(x)ci(x)⩽0,i∈I
1、对数障碍(logarithmic barrier)
使用不等式约束构造对数障碍物添加到目标函数中,转换为无约束优化,如下式所示:
B
ln
(
x
,
σ
)
=
f
(
x
)
−
σ
∑
i
∈
I
ln
(
−
c
i
(
x
)
)
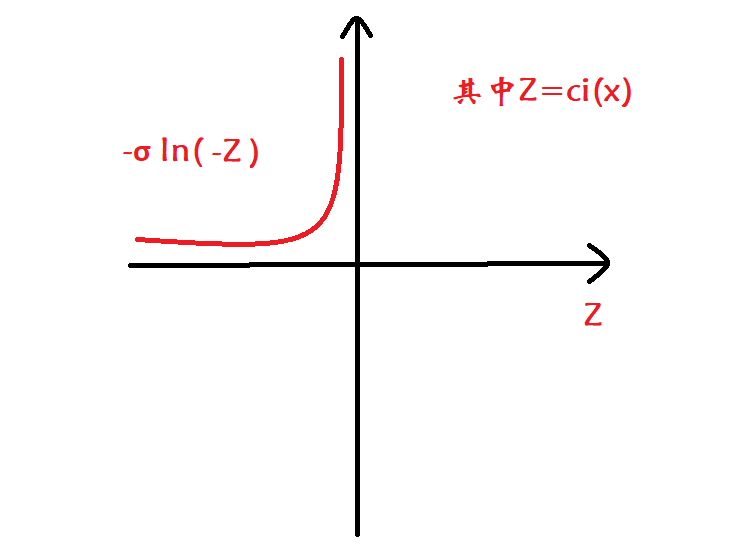
B_{\ln}(x,\sigma)=f(x)-\color{red}{\sigma\sum_{i\in\mathcal{I}}\ln(-c_i(x))}
Bln(x,σ)=f(x)−σi∈I∑ln(−ci(x))
当
c
i
(
x
)
c_i(x)
ci(x)从小于0的方向接近于0时,附加的对数障碍项的值会以log的速率急剧增大,从而使得转换后的无约束优化目标函数更趋向于选择满足不等式约束且离界限0有一定距离的解。
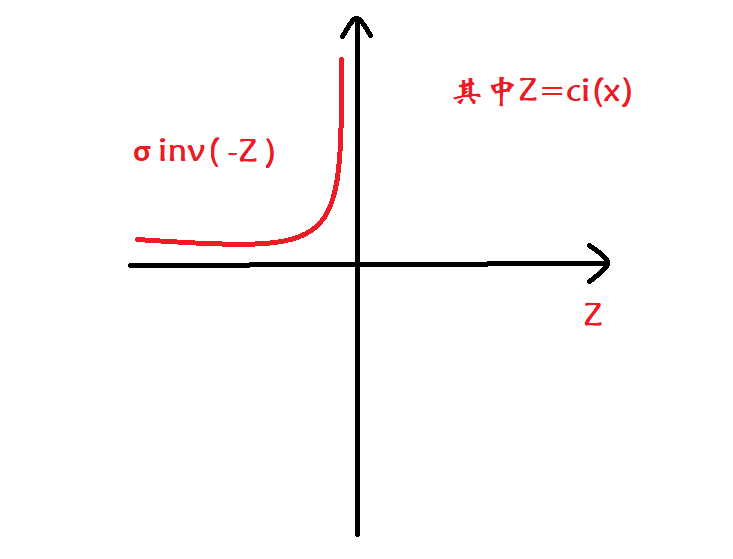
2、逆障碍(inverse barrier)
使用不等式约束构造逆障碍添加到目标函数中,转换为无约束优化,如下式所示:
B i n v ( x , σ ) = f ( x ) + σ ∑ i ∈ I i n v ( − c i ( x ) ) B_{\mathrm{inv}}(x,\sigma)=f(x)+\color{red}{\sigma\sum_{i\in\mathcal{I}}\mathrm{inv}(-c_i(x))} Binv(x,σ)=f(x)+σi∈I∑inv(−ci(x))
其中,inv表示逆或倒数的含义,如下所示
i f z > 0 , i n v ( z ) : = 1 / z i f z < 0 , i n v ( z ) : = i n f \mathrm{~if~}z>0 , \mathrm{~inv}(z):=1/z \\\\\mathrm{~if~}z<0 , \mathrm{~inv}(z):=inf if z>0, inv(z):=1/z if z<0, inv(z):=inf
当 c i ( x ) c_i(x) ci(x)从小于0的方向接近于0时,附加的逆障碍项的值会急剧增大,从而使得转换后的无约束优化目标函数更趋向于选择满足不等式约束且离界限0有一定距离的解。
3、指数障碍(inverse barrier)
使用不等式约束构造指数障碍添加到目标函数中,转换为无约束优化,如下式所示:
B e x p i ( x , σ ) = f ( x ) + σ ∑ i ∈ I e x p i ( − c i ( x ) ) B_{\mathrm{expi}}(x,\sigma)=f(x)+\color{red}{\sigma\sum_{i\in\mathcal{I}}\mathrm{expi}(-c_i(x))} Bexpi(x,σ)=f(x)+σi∈I∑expi(−ci(x))
其中,expi表示指数的含义,如下所示
e x p i ( z ) : = e 1 / z i f z > 0 \mathrm{~expi}(z):=e^{1/z}\mathrm{~if~}z>0 expi(z):=e1/z if z>0
当 c i ( x ) c_i(x) ci(x)从小于0的方向接近于0时,附加的指数障碍项的值会急剧增大,从而使得转换后的无约束优化目标函数更趋向于选择满足不等式约束且离界限0有一定距离的解。
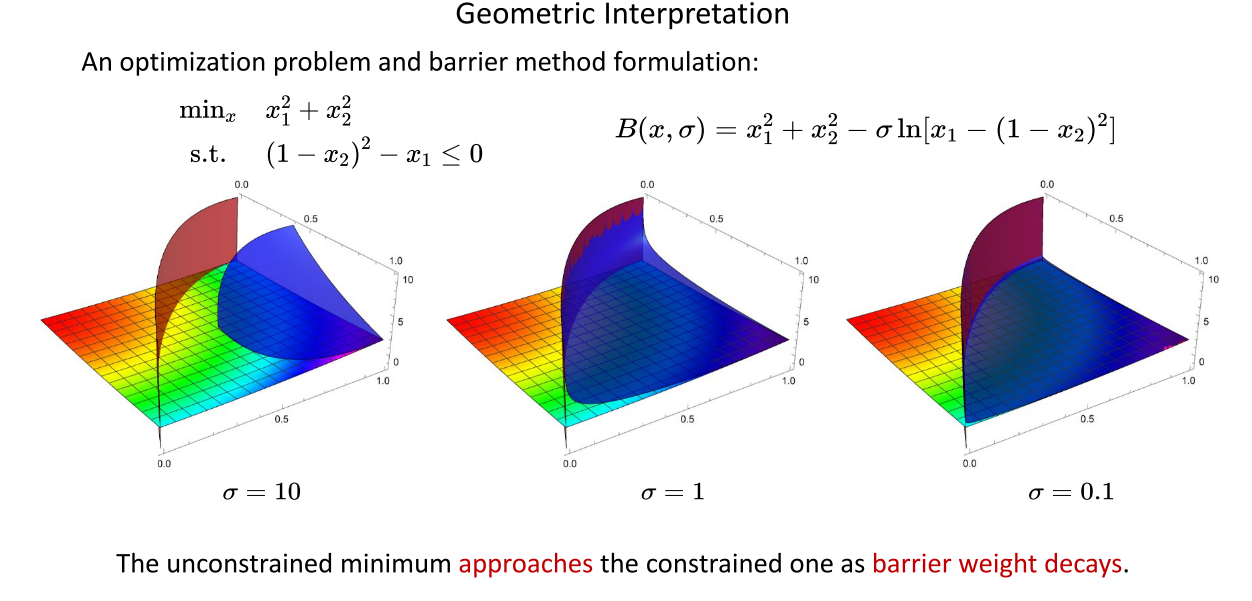
4、障碍函数法特点
当 σ \sigma σ从正向趋于0时,采用障碍函数法将带不等式约束的目标函数转换为无约束的目标函数后,转换前后的最优解几乎相等, σ \sigma σ从正向越接近于0,即随着障碍权值的衰减,无约束最小值趋于约束最小值。下图中的例子,当 σ \sigma σ取0.1时,转换前后的最优解几乎相等。
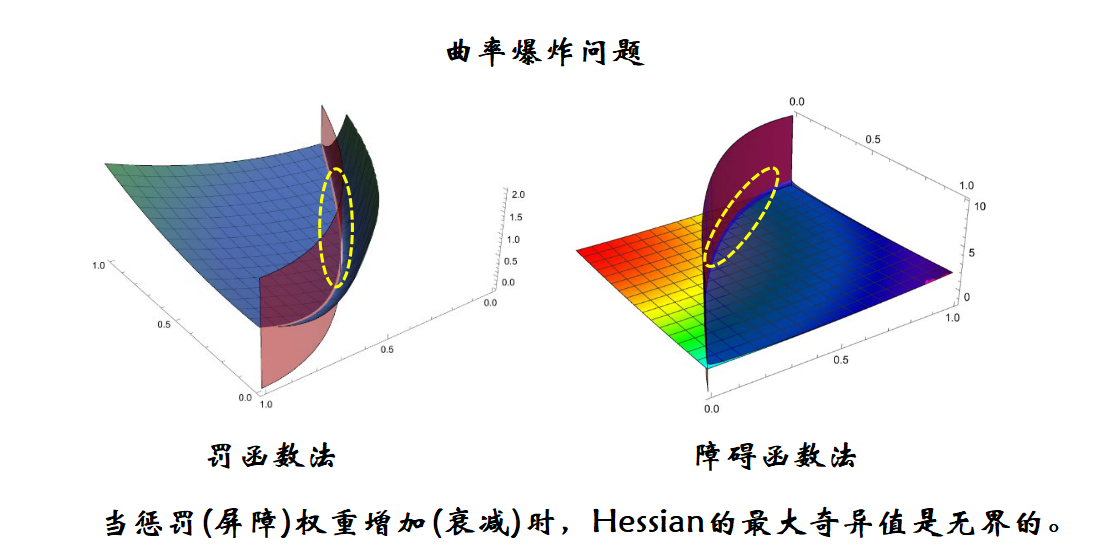
罚函数法随着 σ \sigma σ的增大,在约束边界的外侧罚函数越趋向于直角,障碍函数法随着 σ \sigma σ的减小(从正向趋于0),在约束边界的内侧罚函数越趋向于直角,在这些地方(下图中虚线圈所示的位置)Hessian矩阵的条件数是趋于无穷大的,所以若使用梯度的方法求解转换后的无约束问题,会遇到求解速度越来越慢的问题。
若对于罚函数法一开始 σ \sigma σ的值设为一个较小值,然后随着迭代逐步增大 σ \sigma σ的值,而不是一上来就给一个很大的值,会一定程度上减缓以上问题,同理,对于障碍函数法一开始也不要给一个很小值,而是随着迭代减小 σ \sigma σ值,也可以在一定程度上减缓以上问题。
虽然与罚函数法相比,障碍函数法不能处理等式约束,但是罚函数法可以处理在不等式约束在约束外没有定义的问题,而罚函数法不能处理在约束外没有定义的问题。
二十三、拉格朗日松弛法(Lagrangian Relaxation)
拉格朗日松弛方法是针对带等式约束的凸优化问题而言的,如下式所示的凸优化问题:
min x f ( x ) s . t . A x = b \begin{array}{cc}\min_x&f(x)\\\mathrm{s.t.}&Ax=b\end{array} minxs.t.f(x)Ax=b
构造拉格朗日函数,在目标函数的基础上,增加λ与等式约束Ax-b的内积项,如下式所示
L ( x , λ ) : = f ( x ) + ⟨ λ , A x − b ⟩ \mathcal{L}(x,\lambda):=f(x)+\langle\lambda,Ax-b\rangle L(x,λ):=f(x)+⟨λ,Ax−b⟩
首先,我们需要找一个λ值,使得上述拉格朗日函数取到最大值,对于满足等式约束的x,Ax-b=0,则其与λ的内积必然为0,此时, L ( x , λ ) \mathcal{L}(x,\lambda) L(x,λ)的最大值即为 f ( x ) f(x) f(x),若Ax-b不等于0,比如其值为 [ 1 , − 1 ] T [1,-1]^T [1,−1]T,则必然可以找到一个λ,其值为 k ∗ [ 1 , − 1 ] T = [ k , − k ] T k*[1,-1]^T=[k,-k]^T k∗[1,−1]T=[k,−k]T,此时λ与Ax-b的内积为2k,若k趋于inf,则 L ( x , λ ) \mathcal{L}(x,\lambda) L(x,λ)的最大值即为inf,如下式所示:
max λ L ( x , λ ) = max λ { f ( x ) + ⟨ λ , A x − b ⟩ } = { f ( x ) , A x − b = 0 ∞ , o t h e r w i s e \max_{\lambda}\mathcal{L}(x,\lambda)=\max_{\lambda}\left\lbrace f(x)+\langle\lambda,Ax-b\rangle\right\rbrace=\left\{\begin{aligned} & f(x),Ax-b=0\\ & \infty,\mathrm{otherwise}\end{aligned}\right. λmaxL(x,λ)=λmax{f(x)+⟨λ,Ax−b⟩}={f(x),Ax−b=0∞,otherwise
所以带等式约束的目标函数求解问题,可以转换成如下所示的,先找一个λ值使得拉个朗日方程 L ( x , λ ) \mathcal{L}(x,\lambda) L(x,λ)取得极大值,然后再找一个x,使得 max λ L ( x , λ ) = f ( x ) 或 i n f \max_\lambda\mathcal{L}(x,\lambda)=f(x)或inf maxλL(x,λ)=f(x)或inf取极小值。(当然对于不满足约束inf情况,极小值依然为inf)
min x f ( x ) , s . t . A x = b ⟺ min x max λ L ( x , λ ) \color{red}{\min_xf(x),\mathrm{~s.t.~}Ax=b\quad\Longleftrightarrow\quad\min_x\max_\lambda\mathcal{L}(x,\lambda)} xminf(x), s.t. Ax=b⟺xminλmaxL(x,λ)
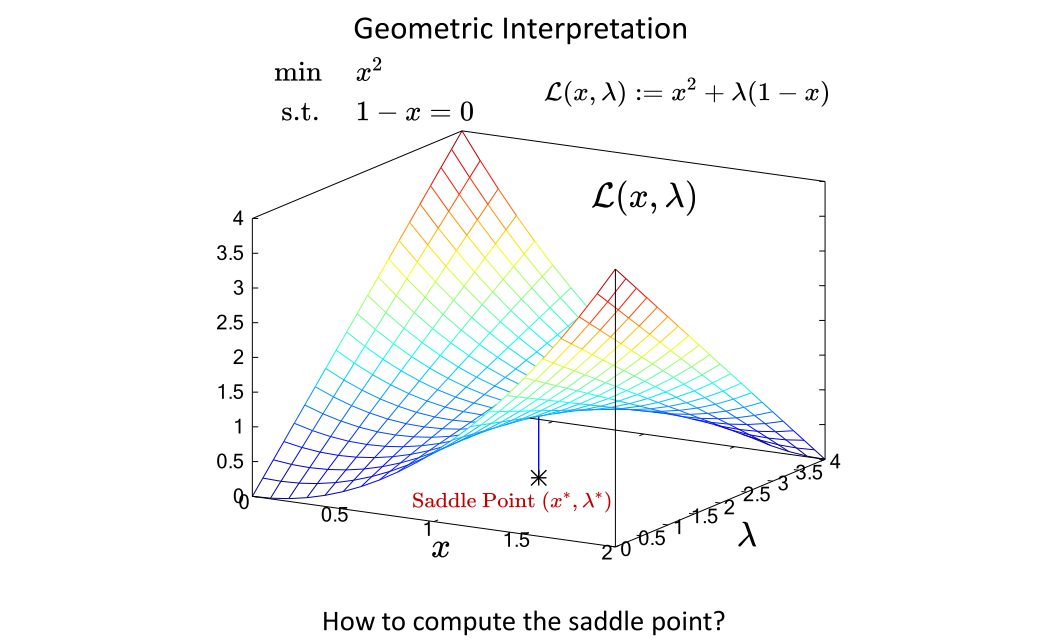
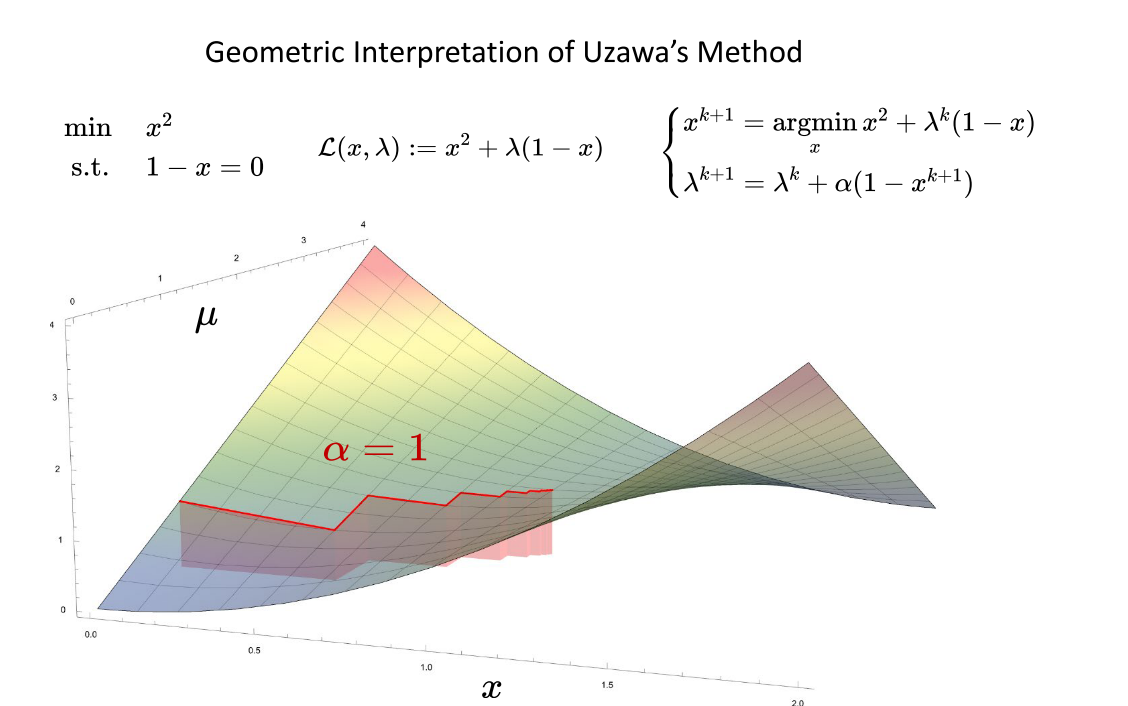
下图中给出一个例子,最优解在 L ( x , λ ) \mathcal{L}(x,\lambda) L(x,λ)的鞍点处,其梯度等于0,Hessian是不定的。、拉格朗日松弛法把带等式约束的问题转换成求鞍点的问题
如果我们不知道f(x)、h(x)的具体表达式,那么我们该如何求呢?现在,我们假设f(x)是严格凸的函数,h(x)是一个线性函数,若直接求 min x max λ L ( x , λ ) \min_x\max_\lambda\mathcal{L}(x,\lambda) minxmaxλL(x,λ),由于求 max λ L ( x , λ ) \max_\lambda\mathcal{L}(x,\lambda) maxλL(x,λ)后得到的值为f(x)或inf,是不连续的,对其再求 min x \min_x minx是不容易的,若交换一下顺序,求 max λ min x L ( x , λ ) \max_\lambda\min_x\mathcal{L}(x,\lambda) maxλminxL(x,λ),由于f(x)是严格凸的,则求 min x L ( x , λ ) \min_x\mathcal{L}(x,\lambda) minxL(x,λ)是一个无约束的最优化问题,可以很好的求出来,对其再求 max λ \max_\lambda maxλ也是一个相对容易得问题。
可以通过以下的迭代式来求解 max λ min x L ( x , λ ) \max_\lambda\min_x\mathcal{L}(x,\lambda) maxλminxL(x,λ),先通过第一个式子计算内层,得到k+1时刻的最优解x,然后利用第二个式子使用梯度上升的方式计算外层的 λ \lambda λ,α是步长, A x k + 1 − b Ax^{k+1}-b Axk+1−b是梯度上升方向。
{ x k + 1 = argmin x L ( x , λ k ) λ k + 1 = λ k + α ( A x k + 1 − b ) \begin{cases}x^{k+1}=\operatorname{argmin}_x\mathcal{L}(x,\lambda^k)\\\lambda^{k+1}=\lambda^k+\alpha(Ax^{k+1}-b)\end{cases} {xk+1=argminxL(x,λk)λk+1=λk+α(Axk+1−b)
这种模式称为Uzawa’s方法
下图中的例子,首先计算内层,即第一个式子的无约束问题的最优化问题,然后再计算外层的 λ \lambda λ,例子中用的步长为1。
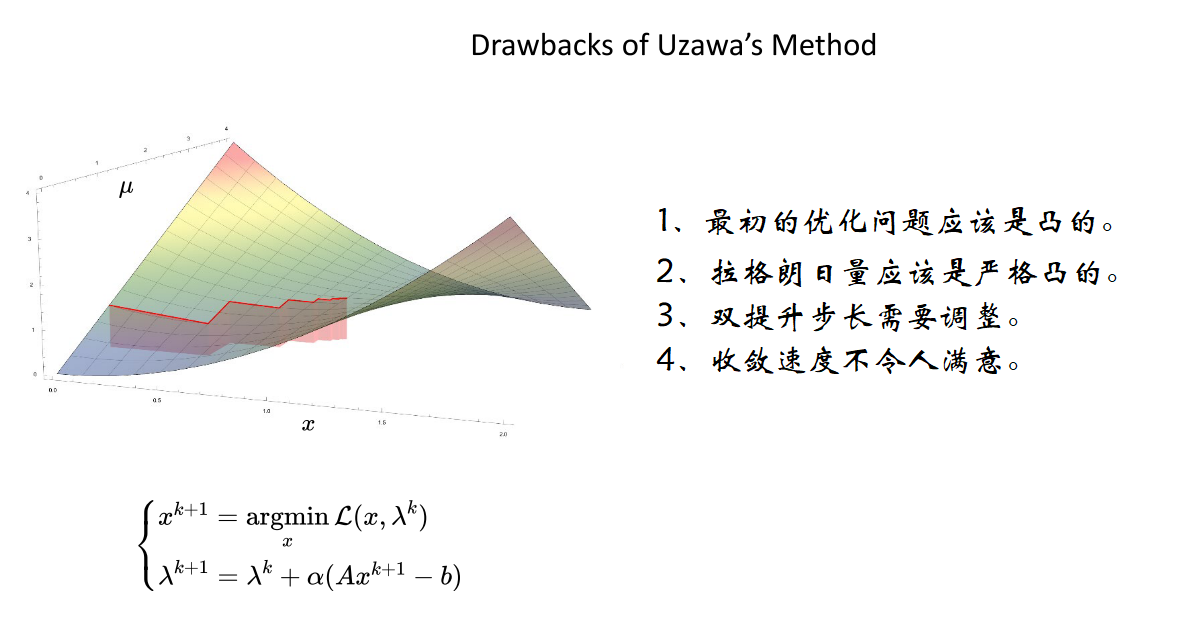
Uzawa’s方法存在下图所介绍的一些缺陷,最初的优化问题应该是凸的、拉格朗日量应该是严格凸的、双提升步长需要调整、收敛速度不令人满意。
参考资料:
1、数值最优化方法(高立 编著)