代码随想录算法训练营第二天| 977.有序数组的平方、 209.长度最小的子数组、 59.螺旋矩阵II。

文章目录

977. 有序数组的平方
- 暴力排序
- 双指针
209.长度最小的子数组
- 暴力求解
- 双指针-滑动窗口 O(n)
59.螺旋矩阵
- 直接模拟
904.水果成篮
- 思路

977. 有序数组的平方

题目描述：给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。
示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 已按 非递减顺序 排序

**进阶：**请你设计时间复杂度为 O(n) 的算法解决本问题

暴力排序

先计算每个数的平方，再用qsort函数排序,时间复杂度为O(n+nlogn)

int cmp(const void *a,const void *b){
    return *(int*)a-*(int*)b;
}
int* sortedSquares(int* nums, int numsSize, int* returnSize) {
    for(int i=0;i<numsSize;i++){
        nums[i]=nums[i]*nums[i];
    }
    qsort(nums,numsSize,sizeof(int),cmp);
    *returnSize=numsSize;
    return nums;
}

双指针

数组是有序的，但是负数的平方有可能成为最大值，故可以采用双指针，每次与数组最后一个元素的平方做比较，时间复杂度0(n)

int* sortedSquares(int* nums, int numsSize, int* returnSize) {
    int *ans=(int*)malloc(sizeof(int)*numsSize);
    int i=numsSize-1;
    int left=0,right=numsSize-1;
    while(left<=right){ //这里要等号，因为最后是处理两个元素，否则ans[0]没有值
        if(nums[left]*nums[left]>nums[right]*nums[right]){
            ans[i--]=nums[left]*nums[left];
            left++;
        }else{
            ans[i--]=nums[right]*nums[right];
            right--;
        }
    }
    *returnSize=numsSize;
    return ans;
}

209.长度最小的子数组

题目链接：209. 长度最小的子数组 - 力扣（LeetCode）

题目描述：给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

暴力求解

两个for循环 O(n^2)

int minSubArrayLen(int target, int* nums, int numsSize){
    //初始化最小长度为INT_MAX
    int minLength = INT_MAX;
    int left, right;
    for(left = 0; left < numsSize; left++) {
        //每次遍历都清零sum，计算当前位置后和>=target的子数组的长度
       int sum = 0;
        //从left开始，sum中添加元素
        for(right = left; right < numsSize; right++) {
            sum += nums[right];
            //若加入当前元素后，和大于target，则更新minLength
            if(sum >= target) {
                int subLength = right - left + 1;
                minLength = minLength < subLength ? minLength : subLength;
            }
        }
    }
    //若minLength不为INT_MAX，则返回minLnegth
    return minLength == INT_MAX ? 0 : minLength;
}

双指针-滑动窗口 O(n)

在暴力解法中，是一个for循环起始位置，一个for循环为终止位置，用两个for循环完成了一个不断搜索区间的过程。

可以利用双指针组成滑动窗口，把两个for循环降低成一个循环。所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出想要的结果。

唯一的一个循环用来改变终止位置，当满足题目所给条件，即窗口内元素之和等于目标值时，更新起始位置

int minSubArrayLen(int target, int* nums, int numsSize) {
    int sum=0;
    int i=0,j=0;
    int min=INT_MAX;
    while(j<numsSize){ //右边界向右扩展
        sum+=nums[j];
        while(sum>=target){ //当sum的值大于等于target时，更新长度，并收缩左边界
            int cur=j-i+1;
            min=cur<min?cur:min;
            sum-=nums[i];
            i++;
        }
        j++;
    }
    return min==INT_MAX?0:min;
}

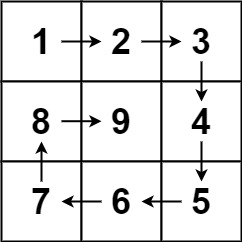
59.螺旋矩阵

题目链接：59. 螺旋矩阵 II - 力扣（LeetCode）

题目描述：给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：1 <= n <= 20

直接模拟

要注意边界问题，坚持循环不变量，比如左右边界定义为[0,n-1]即左闭右闭，模拟循环时就要坚持使用<=；如果是左闭右开，要注意右边界和下边界减一

int** generateMatrix(int n, int* returnSize, int** returnColumnSizes) {
    *returnSize=n;
    *returnColumnSizes = (int*)malloc(sizeof(int) * n);
    int **ans=(int**)malloc(sizeof(int*)*n);
    for(int i=0;i<n;i++){
        ans[i]=(int*)malloc(sizeof(int)*n);
        (*returnColumnSizes)[i]=n;
    }
    int left=0,right=n-1; //左右边界
    int top=0,bottom=n-1; //上下边界
    int num=1;
    while(num<=n*n){
        for(int i=left;i<=right;i++){//从左至右
            ans[left][i]= num++;
        }
        top++; //更新上边界
        for(int i=top;i<=bottom;i++){//从上至下
            ans[i][right]=num++;
        }
        right--; //更新右边界
        for(int i=right;i>=left;i--){//从右至左
            ans[bottom][i]=num++;
        }
        bottom--; //更新下边界
        for(int i=bottom;i>=top;i--){//从下至上
            ans[i][left]=num++;
        }
        left++; //更新左边界
    }
    return ans;
}

904.水果成篮

题目链接：904. 水果成篮 - 力扣（LeetCode）

题目描述：你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果种类。

你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：

你只有两个篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
你可以选择任意一棵树开始采摘，你必须从每棵树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。

给你一个整数数组 fruits ，返回你可以收集的水果的最大数目。

示例 1：

输入：fruits = [1,2,1]
输出：3
解释：可以采摘全部 3 棵树。

示例 2：

输入：fruits = [0,1,2,2]
输出：3
解释：可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。

示例 3：

输入：fruits = [1,2,3,2,2]
输出：4
解释：可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。

示例 4：

输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出：5
解释：可以采摘 [1,2,1,1,2] 这五棵树。

提示：

1 <= fruits.length <= 105
0 <= fruits[i] < fruits.length

思路

滑动窗口+哈希寻找最长的连续子数组，且该子数组内只有两种类型的水果

由于fruits[i] 是有限的，可以用数组代替哈希表

#define MAX_SIZE 100000
int totalFruit(int* fruits, int fruitsSize) {
    if(fruitsSize<=2) return fruitsSize;
    int type1=-1,type2=-1; //初始两个篮子的水果种类，都为-1
    int ans=0,cnt=0;//记录最大长度和实时长度
    int left=0,right=0;//左右指针
    int hash[MAX_SIZE]={0};//数组哈希表记录水果种类和个数
    while(right<fruitsSize){
        //第right棵树上的水果种类已经在篮子里了，直接计数
        if(fruits[right]==type1||fruits[right]==type2){
           cnt++;
           hash[fruits[right]]++;
        }else{//该水果种类未记录
            if(type1==-1){//有空篮子1
                type1=fruits[right];
                cnt++;
                hash[fruits[right]]++;
            }else if(type2==-1){//有空篮子2
                type2=fruits[right];
                cnt++;
                hash[fruits[right]]++;
            }else{//没有空蓝子，需要腾出一个
               //要腾出一个位置，当两个篮子均不为空时不断丢出从第left树上装入的水果
                //直到把一个篮子丢空
                while(hash[type1]*hash[type2]!=0){
                    hash[fruits[left]]--;
                    left++;
                    cnt--;
                }
                //更新种类
                type1=hash[type1]==0?-1:type1;
                type2=hash[type2]==0?-1:type2;
                right--;//返回到当前指针
            }
        }
        ans=ans>cnt?ans:cnt;//更新最长长度
        right++;
    }
    return ans;
}