两种聚类方法——K均值聚类（K-means）算法和模糊C均值聚类（FCM）算法的简述与在MATLAB中的实现

在科学计算领域，聚类算法一般都是作为其他算法分析的基础，对数据进行聚类可以从整体上分析数据的一些特性。聚类有很多的算法，K-means是最简单最实用的一种算法，FCM算法则是K-means算法融合模糊理论的一种改进算法。本文将简述这两种算法，并在MATLAB中实现这两种算法对数据的聚类。

1.K-means算法

1.1算法流程

K-means算法是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。
1.首先确定一个k值，即我们希望将数据集经过聚类得到k个集合。
2.从数据集中随机选择k个数据点作为聚类中心。
3.对数据集中每一个点，计算其与每一个聚类中心的距离（如欧式距离），离哪个聚类中心近，就划分到那个聚类中心所属的集合。
4.把所有数据归好集合后，一共有k个集合。然后重新计算每个集合的聚类中心。
5.如果新计算出来的聚类中心和原来的聚类中心之间的距离小于某一个设置的阈值（表示重新计算的聚类中心的位置变化不大，趋于稳定），我们可以认为聚类已经达到期望的结果，算法终止。
6.如果新聚类中心和原聚类中心距离变化很大，需要迭代3至5步骤。

1.2程序实现

下面是在MATLAB中实现K-means算法的程序。
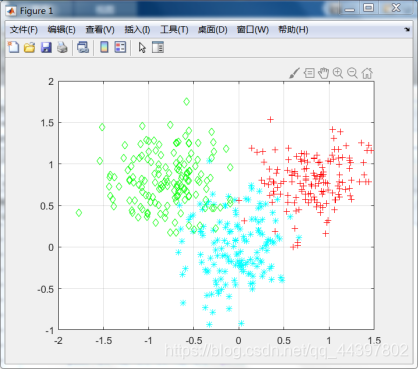
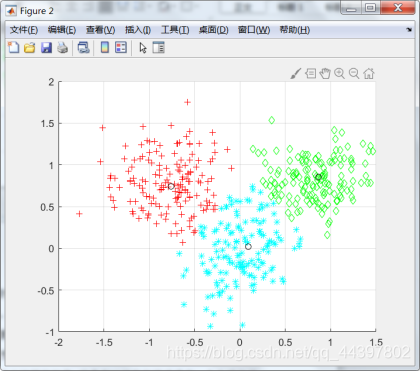
这里使用的数据集dataSet由3个各150个样本的高斯分布组成，后面FCM算法的实现也是如此。程序中设置聚类数为3，初始类中心为迭代开始前在数据集中随机生成，随后计算样本点到每一个类中心距离，这里的距离选取的是欧氏距离，最后按标号将数据分类，求各类中心距离的平均值。程序设置的迭代终止条件是循环100次。迭代结束后将3类样本点以不同颜色显示区分，并标出类中心。

%第一类数据
a=[0 0 ];  
S1=[.1 0 ;0 .1];  
data1=mvnrnd(a,S1,150);   %产生高斯分布数据
%第二类数据
b=[0.8 0.8 ];
S2=[.1 0 ;0 .1];
data2=mvnrnd(b,S2,150);
%第三类数据
c=[-0.8 0.8 ];
S3=[.1 0 ;0 .1];
data3=mvnrnd(c,S3,150);
%显示数据
plot(data1(:,1),data1(:,2),'c*');
hold on;
plot(data2(:,1),data2(:,2),'r+');
plot(data3(:,1),data3(:,2),'gd');
grid on;
%三类数据合成一个不带标号的数据集
dataSet=[data1;data2;data3]; 
 
%K-means 聚类
N=3;
[m, n] = size(dataSet);
re = zeros (m, n+1);
center = zeros(N, n);
%初始化聚类中心
%设置聚类数目
re(:, 1:n) = dataSet(:,:);
for x=1:N
    center (x, :) =dataSet( randi (450, 1), :); %第一次随机产生聚类中心
end
for i = 1:100
    distence=zeros(1, N);
    num=zeros(1, N);
    new_center=zeros(N, n);
%更新c
for x=1:m
    for y=1:N
        distence(y) =norm(dataSet(x, :)-center(y, :));%计算到每个类的距离
    end
    [~, temp] =min(distence);%求最小的距离
    re(x, n+1)=temp;
end
 
    k=0;
    for y=1:N
        for x=1:m
            if re (x, n+1)==y
               new_center(y, :)=new_center(y, :)+re(x, 1:n);
               num(y)=num(y)+1;
            end
        end
        new_center(y, :)=new_center(y, :)/num(y);
        if norm(new_center (y, :) -center (y, :)) <0.1
            k=k+1;
        end
    end
    if k==N
        break;
    else
        center=new_center;
    end
end
[m, n]=size(re); 
%最后显示聚类后的数据
figure;
hold on;
for i=1:m
    if re(i,n) ==1
        plot (re (i, 1), re (i, 2),' c*');
        plot (center (1, 1), center (1, 2),' ko');
    elseif re(i, n) ==2
        plot (re (i, 1), re (i, 2),' r+');
        plot (center (2, 1), center (2, 2),' ko');
    elseif re(i, n) ==3
        plot (re (i, 1), re (i, 2),' gd');
        plot (center (3, 1), center (3, 2),' ko');
    else
        plot (re (i, 1), re (i, 2),' m*');
        plot (center (4, 1), center (4, 2),' ko');
    end
end
grid on

1.3实验结果

原始数据集

在这里插入图片描述

聚类结果

在这里插入图片描述

2.FCM算法

2.1算法流程

FCM算法融合了模糊理论的精髓，相较于k-means的硬聚类，模糊c提供了更加灵活的聚类结果。因为大部分情况下，数据集中的对象不能划分成为明显分离的类，指派一个对象到一个特定的类有些生硬，也可能会出错。因此FCM对每个对象和每个类赋予一个权值即隶属度，指明对象属于该类的程度。当然，基于概率的方法也可以给出这样的权值，但是有时候我们很难确定一个合适的统计模型，因此使用具有自然地、非概率特性的FCM算法就是一个比较好的选择。该方法由Dunn在1973年提出，并由Bezdek在1981年改进，在模式识别被频繁使用。
FCM算法的隶属度U_ij指样本j在类i的隶属度，根据FCM算法的规定样本在各类的隶属度之和为1。
$\sum_{i=1}^{c}u_{ij}=1, j=1,2,...,n$

隶属度的迭代公式如下：
$u_{ij}=\frac{1}{\sum_{k=1}^{C}\left ( \frac{\left || x_{ij}-c_{j} \right || }{\left || x_{i}-c_{k}\right ||} \right ) ^{\frac{2}{m-1} }}$

FCM算法的目标是使得下式——目标函数J收敛于某值或低于某一阈值或两次迭代的J之差低于某值又或是达到规定的迭代次数，此时终止运算。
$J=\sum_{i=1}^{c}\sum_{j=1}^{n}u_{ij}^{m}\left | \left | x_{j}-c_{i} \right | \right | ^{2}$
1.初始化：通常采用随机初始化。即隶属度随机地选取。类数需要人为选定。
2.计算聚类中心：FCM中的聚类中心有别于传统聚类中心的地方在于，它是以隶属度为权重做一个加权平均。聚类中心的迭代公式如下：
$C_{j}=\frac{\sum_{i=1}^{N}u_{ij}^{m}\times x_{i} }{\sum_{i=1}^{N}u_{ij}^{m} }$
3.更新聚类划分：即更新权重（隶属度）。简单地说，如果样本点越靠近聚类中心，则隶属度越高，反之越低。

2.2程序设计

下面是在MATLAB中实现FCM算法的程序。
这里使用的数据集同K-means算法程序中使用的数据集，程序包括一个FCM算法的子函数和主程序。FCM子函数包括num_data、num_clusters、iter、m和dataSet等5个输入项，分别是样本个数、类别数、迭代次数、指数和数据集；函数包括c、U、J等3个输出项，分别是聚类中心、隶属度矩阵和目标函数值。因为聚类中心的计算公式中需要样本在各类的隶属度，程序中先定义了一个满足隶属度约束条件的初始隶属度矩阵，而后进行聚类中心的计算。聚类中心更新后将计算此时的目标函数，目标函数中的距离度量选取的是欧氏距离。最后更新当前的隶属度矩阵，到这里一次迭代结束。
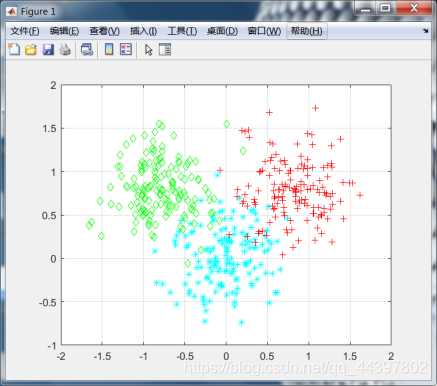
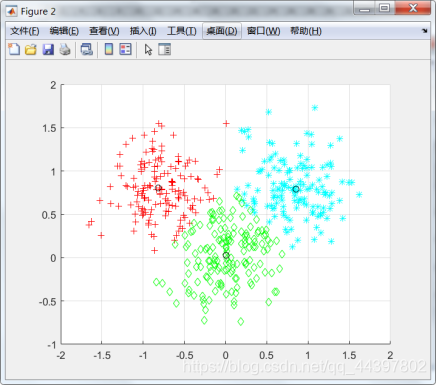
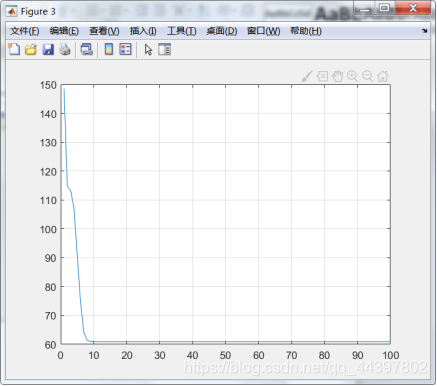
主程序里设置的分类数为3，,设置的迭代终止条件是循环100次。程序将显示原始数据集、聚类结果和目标函数J的变化图像。

FCM子函数

function [c, U,J] = FCM(num_data,num_clusters,iter,m,dataSet)  
%--初始化隶属度u，条件是每一列和为1 
U = rand(num_clusters,num_data);
col_sum = sum(U);
U = U./col_sum; 
% 循环--规定迭代次数作为结束条件
for i = 1:iter
    %更新c
    for j = 1:num_clusters
        u_ij_m = U(j,:).^m;
        sum_u_ij = sum(u_ij_m);
       c(j,:) = u_ij_m*dataSet./sum_u_ij;
    end
    %-计算目标函数J
    temp1 = zeros(num_clusters,num_data);
    for j = 1:num_clusters
        for k = 1:num_data
            temp1(j,k) = U(j,k)^m*(norm(dataSet(k,:)-c(j,:)))^2;
        end
    end
    J(i) = sum(sum(temp1));
    %更新U
    for j = 1:num_clusters
        for k = 1:num_data
            sum1 = 0;
            for j1 = 1:num_clusters
                temp = (norm(dataSet(k,:)-c(j,:))/norm(dataSet(k,:)-c(j1,:))).^(2/(m-1));
                sum1 = sum1 + temp;
            end
            U(j,k) = 1./sum1;
        end
    end
end

主函数

%第一类数据
a=[0 0 ];  
S1=[.1 0 ;0 .1];  
data1=mvnrnd(a,S1,150);   %产生高斯分布数据
%第二类数据
b=[0.8 0.8 ];
S2=[.1 0 ;0 .1];
data2=mvnrnd(b,S2,150);
%第三类数据
c=[-0.8 0.8 ];
S3=[.1 0 ;0 .1];
data3=mvnrnd(c,S3,150);
%显示数据
plot(data1(:,1),data1(:,2),'c*');
hold on;
plot(data2(:,1),data2(:,2),'r+');
plot(data3(:,1),data3(:,2),'gd');
grid on;
%三类数据合成一个不带标号的数据类
dataSet=[data1;data2;data3]; 
 
num_clusters = 3;%类别数
iter = 100;%迭代次数
m = 2;%指数
num_data = size(dataSet,1);%样本个数
[c, U,J] = FCM(num_data,num_clusters, iter,m,dataSet);
figure;
[m,o] = max(U); %找到所属的类
index1 = find(o==1);   %索引第一类
index2 = find(o==2); 
index3 = find(o==3);
hold on,plot(dataSet(index1, 1),dataSet(index1, 2),'c*');  %画出来
hold on,plot(dataSet(index2, 1),dataSet(index2, 2),'r+');  
hold on,plot(dataSet(index3, 1),dataSet(index3, 2),'gd');  
plot(c(:,1),c(:,2),'ko');
grid on
figure;
plot(J);
grid on