【C语言】红黑树

红黑树

1.二叉查找树

首先要了解的是二叉查找树，也称为二叉排序树，优点是在节点均匀分布的情况下，查找效率更高，缺点是，如果节点分布在一侧，查找时间就会约等于数组从头到尾的去查找。

二叉查找树的子树都是二叉查找树。
左子树都小于根节点，右子树都大于根节点

2.平衡二叉查找树

其次，平衡二叉查找树，也称为AVL树，AVL是它的两个发明者的名字组成。它有一套插入，删除的平衡机制，让插入删除后使用相应的平衡算法，再次成为AVL树，这样可以让每次的最坏查找时间接近O(logn)，缺点是用于平衡的开销太大。

AVL树的子树都是AVL树
左右子树的高度差小于等于1

3.红黑树

红黑树(Red Black Tree)是一种二叉查找树，它并不是严格意义上的平衡二叉树，因为它有自己的平衡规则，和平衡二叉树规则不一样。它的查找，插入，删除的时间复杂度都是O(logn),n是指树中元素的个数。因此它在查找，插入，删除的最坏情况下运行时间很好。

为什么查找，插入，删除的复杂度都是O(logn),因为红黑树自己有一套规则，去保持红黑树插入删除后还是红黑树。红黑树的平衡次数，相对于普通平衡二叉树少，开销更小。

结点是红色或黑色（一个节点要么是红色，要么是黑色）
根结点是黑色
所有叶子都是黑色。（叶子是NIL结点）
每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）
从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

红黑树用在哪些地方：hashmap，cfs，epoll，定时器，nginx中

使用红黑树，

第一，主要是使用它的(key，value)属性，使用key可以去树上查找相应的value

第二，它是一个二叉排序树，中序遍历是顺序的，可以查一个范围，例如比某个key小的有哪些

1.定义一颗红黑树

typedef int KEY_TYPE;
//定义红黑树节点
typedef struct _rbtree_node
{
	KEY_TYPE key;
	void *value;
	struct _rbtree_node *right;
	struct _rbtree_node *left;
	struct _rbtree_node *parent;
	unsigned char color;
} rbtree_node;

//定义红黑树
typedef struct _rbtree
{
    //红黑树的根
	rbtree_node *root;
    //红黑树叶子节点
	rbtree_node *nil;
} rbtree;

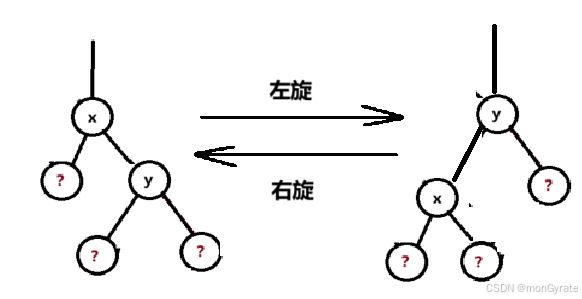
2. 红黑树旋转

红黑树的插入，删除，会导致不平衡，需要旋转和变色
在这里插入图片描述

2.1 左旋

这里仅仅是旋转，是因为不满足上述5条红黑树性质而进行的旋转。与平衡二叉树的旋转不一样。

因此，只需要考虑旋转点与它的父节点之间的左旋。

// T是树根节点，x是旋转轴节点的父节点
void rbtree_left_rotate(rbtree *T, rbtree_node *x)
{
	//y为旋转轴节点
	rbtree_node *y = x->right; 

	x->right = y->left;
	if (y->left != T->nil)
	{
		y->left->parent = x;
	}

	y->parent = x->parent; 
	if (x->parent == T->nil)
	{
		T->root = y;
	}
	else if (x == x->parent->left)
	{
		x->parent->left = y;
	}
	else
	{
		x->parent->right = y;
	}

	y->left = x;
	x->parent = y;
}

2.2 右旋

将左旋代码的x改为y，left改为right即可