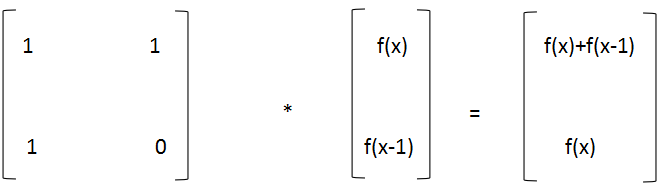一，简介

线性代数中有：

**也就表明：**图中所表示的可以理解为 f（x+1）=f（x）+f（x-1）即斐波那契数列的通式，若要求项数较大的数n斐波那契数，那么只用将矩阵A进行n-1次幂运算

#include<iostream>
#include<cstdio>
#define Mod 10000

using namespace std;

struct Mtr{
	int f[2][2];
	void init1(){
	//构造矩阵 
		f[0][0] = f[0][1] = f[1][0] = 1;
		f[1][1] = 0;
	}
	void init2(){
	//单位矩阵 A*E=A 
		f[0][0] = f[1][1] = 1;
		f[1][0] = f[0][1] = 0;
	}
};

Mtr mulMtr(Mtr a, Mtr b){
	Mtr ans;
	int i, j, k;
	for(i = 0; i < 2; i++){
		for(j = 0; j < 2; j++){
			ans.f[i][j] = 0;
			for(k = 0; k < 2; k++){
				ans.f[i][j] += a.f[i][k] * b.f[k][j];
			}
			ans.f[i][j] %= Mod;
		}
	}
	return ans;
}
//快速幂
Mtr QuickPowMtr(Mtr a, int b){
	Mtr ans;
	ans.init2();
	while(b){
		if(b & 1){
			ans = mulMtr(ans, a);
		}
		b >>= 1;
		a = mulMtr(a, a);
	}
	return ans;
}
int main(){
	
	int n;
//	cin >> n;
	while(cin >> n && n != -1){
		if(n == 0) cout << 0 << endl;
		else{
			Mtr t;
			t.init1();
			Mtr a = QuickPowMtr(t, n+1);
			cout << a.f[1][1] << endl;
		}
	} 
	
	return 0;
}