214. 最短回文串 - 力扣（LeetCode）

文章起笔：2021年11月2日15:25:01

问题描述及示例

给定一个字符串 s，你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。

示例 1：
输入：s = “aacecaaa”
输出：“aaacecaaa”

示例 2：
输入：s = “abcd”
输出：“dcbabcd”

提示：
0 <= s.length <= 5 * 10⁴
s 仅由小写英文字母组成

我的题解

这道题的关键其实就是寻找 s 中的最长回文前缀子串。注意，该子串一定要是前缀子串，且该子串有回文特征。

所谓“前缀子串”，可以把它理解为该子串的第一个字符必须是 s 的第一个字符。

找到上述子串后（假设为 sub），将 s 中除去 sub 部分的剩余子串复制一份再拼接到原 s 字符串前所得到的就是我们要的结果。

成功前的尝试

我的第一反应就是之前做过的一道题目：

参考：【算法-LeetCode】5. 最长回文子串（动态规划）_赖念安的博客-CSDN博客

上面这道题也涉及到寻找最长回文子串的问题。我一开始没有多想，就直接照搬了上面的这个题解的思路，结果发现无法通过：

/**
 * @param {string} s
 * @return {string}
 */
var shortestPalindrome = function(s) {
  let dp = new Array(s.length).fill(0).map(
    () => new Array(s.length).fill(true)
  );
  let range = [0, 0];
  for(let i = s.length - 2; i >= 0; i--) {
    for(let j = s.length - 1; j >= 1; j--) {
      if(i > j) {
        continue;
      }
      dp[i][j] = s[i] === s[j] && dp[i+1][j-1];
      if(dp[i][j] && range[1] - range[0] < j - i) {
        range[0] = i;
        range[1] = j;
      }
    }
  }
  if(range[0] === 0) {
    return s.slice(range[1]+1).split('').reverse().join('') + s;
  } else {
    return s.slice(1).split('').reverse().join('') + s;
  }
  // return s.slice(range[0], range[1]+1);
};


提交记录
执行结果：解答错误
通过测试用例：112 / 120
输入："aabba"
输出："abbaaabba"
预期结果："abbaabba"
时间：2021/11/02 15:25

原因就是我没有限制所找到的回文子串必须是“前缀子串”。所以我加上了这个限制：

/**
 * @param {string} s
 * @return {string}
 */
var shortestPalindrome = function(s) {
  let dp = new Array(s.length).fill(0).map(
    () => new Array(s.length).fill(true)
  );
  let range = [0, 0];
  for(let i = s.length - 2; i >= 0; i--) {
    for(let j = s.length - 1; j >= 1; j--) {
      if(i > j) {
        continue;
      }
      dp[i][j] = s[i] === s[j] && dp[i+1][j-1];
      // 加上了 i === 0 这个限制条件，保证所找到的回文子串是前缀子串
      if(dp[i][j] && range[1] - range[0] < j - i && i === 0) {
        range[0] = i;
        range[1] = j;
      }
    }
  }
  return s.slice(range[1]+1).split('').reverse().join('') + s;
};


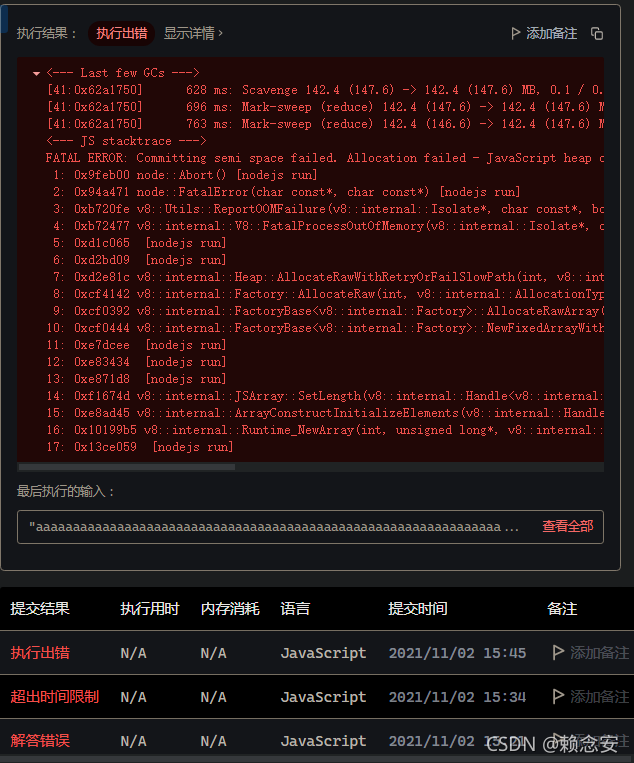
执行结果：超出时间限制
最后执行的输入：
"aaaaaaaaaaaaaaaaaaaaaa...aaaaaaaaaaaaaaaaaaaaaaaaa"
时间：2021/11/02 15:34

结果还是没法儿通过，所有用例：

所以上面的解法虽然说理论上是可行的，但是遇到较长的用例时，还是没办法在规定时间内处理。

于是我又怀着侥幸心理在程序的最前面加上了下面这个判断条件：

if(s.split('').reverse().join('') === s) {
  return s;
}

结果发现还是解答错误：

暴力解法

既然上面的方法没法通过，我就尝试着用暴力解法。

暴力解法就是在由前至后遍历 s 的同时，判断当前前缀子串是否为回文子串。找到最长的那个回文子串的结束位置 end。之后的套路就和上面讲到的一样了。

暴力解法1（由前往后；超时）

/**
 * @param {string} s
 * @return {string}
 */
var shortestPalindrome = function(s) {
  let end = 0;
  for(let i = 1; i < s.length; i++) {
    end = isPalindrome(s.slice(0,i + 1)) ? i : end;
  }
  return s.slice(end + 1).split('').reverse().join('') + s;

  function isPalindrome(str) {
    return str.split('').reverse().join('') === str;
  }
};


执行结果：超出时间限制
最后执行的输入：
"aaaaaaaaaaaaaaaaaaaaaa...aaaaaaaaaaaaaaaaaaaaaaaaa"
时间：2021/11/03 10:51

结果还是那个超长的用例因为超时而没有通过。

暴力解法2（由后往前；通过）

仔细想了想，发现上面那种由前往后的暴力遍历方法其实没必要。我们可以用一个 s 翻转后的辅助字符串 reversedStr 来帮助我们判断最长的回文前缀子串。并且不用等到遍历完所有的字符才结束，当在遍历过程中发现了符合回文特征的前缀子串后就可以立马返回结果了。

/**
 * @param {string} s
 * @return {string}
 */
var shortestPalindrome = function(s) {
  if(!s.length) {
    return s;
  }
  let reversedStr = s.split('').reverse().join('');
  for(let i = 0, len = s.length; i < len; i++) {
    if(s.slice(0, len - i) === reversedStr.slice(i)) {
      return s.slice(len - i).split('').reverse().join('') + s;
    }
  }
};

提交记录
状态：通过
120 / 120 个通过测试用例
执行用时：76 ms, 在所有 JavaScript 提交中击败了81.31%的用户
内存消耗：41.2 MB, 在所有 JavaScript 提交中击败了56.07%的用户
时间：2021/11/03 11:59

KMP

一开始我并没有想到用 KMP 算法来解决这个问题，看了题解区的解答后才知道原来还可用这个思路。

但是本题中其实并没有用到 KMP 算法中的全部思想，只是借用了里面 生成前缀表 的这部分思路。

核心思路就是先人为构造一个模式字符串 str，这个 str 是由原来的 s 和 s 的翻转结果拼接而成的。

当然，为了适应题目的要求，在拼接这两部分字符串时，还在两字符串中间加上了一个干扰字符 #，这个干扰字符可以随意取，只要不是小写英文字母就可以。

这个 str 的最长前后缀相同子串就是我们要找的那个回文子串。

所以在了解了 KMP 算法中生成前缀表的逻辑后再理解下面的题解的话就容易多了。

可以在下方的【有关参考】中查看相关的讲解。

/**
 * @param {string} s
 * @return {string}
 */
var shortestPalindrome = function (s) {
  let str = s + '#' + s.split('').reverse().join('');
  let start = generatePrefixTable(str)[str.length - 1];
  return s.slice(start).split('').reverse().join('') + s;

  /**
   * @description: 生成匹配模式串 pattern 的前缀表
   * @param {String} pattern
   * @return {Array} prefixTab
   */
  function generatePrefixTable(pattern) {
    // prefixTab 是最终生成的前缀表
    let prefixTab = [0];
    // front 是当前子串的前缀末尾索引
    let front = 0;
    // back 是当前子串的后缀末尾索引
    for (let back = 1; back < pattern.length; back++) {
      while (front > 0 && pattern[front] !== pattern[back]) {
        front = prefixTab[front - 1];
      }
      if (pattern[front] === pattern[back]) {
        front++;
      }
      prefixTab[back] = front;
    }
    return prefixTab;
  }
};


提交记录
状态：通过
120 / 120 个通过测试用例
执行用时：84 ms, 在所有 JavaScript 提交中击败了57.01%的用户
内存消耗：43.6 MB, 在所有 JavaScript 提交中击败了24.30%的用户
时间：2021/11/03 16:55

官方题解

更新：2021年7月29日18:43:21

因为我考虑到著作权归属问题，所以【官方题解】部分我不再粘贴具体的代码了，可到下方的链接中查看。

【更新结束】

更新：2021年11月3日12:03:52

参考：最短回文串 - 最短回文串 - 力扣（LeetCode）

【更新结束】

有关参考

更新：2021年11月3日12:04:35
参考：图解KMP算法 - 最短回文串 - 力扣（LeetCode）
参考：「手画图解」从简单的暴力法想到 KMP - 最短回文串 - 力扣（LeetCode）
更新：2021年11月3日12:05:26
参考：帮你把KMP算法学个通透！（理论篇）_哔哩哔哩_bilibili
参考：帮你把KMP算法学个通透！（求next数组代码篇）_哔哩哔哩_bilibili
参考：KMP字符串匹配算法1_哔哩哔哩_bilibili
参考：KMP字符串匹配算法2_哔哩哔哩_bilibili
参考：【搬运】油管阿三哥讲KMP查找算法，中英文字幕，人工翻译，简单易懂_哔哩哔哩_bilibili
更新：2021年11月3日17:39:20
参考：【算法-LeetCode】5. 最长回文子串（动态规划）_赖念安的博客-CSDN博客