目录
1. 介绍
本章需要完成的任务是,用线性神经网络对sin函数进行拟合。不使用pytorch提供的nn模块,也不能使用tensor的反向传播
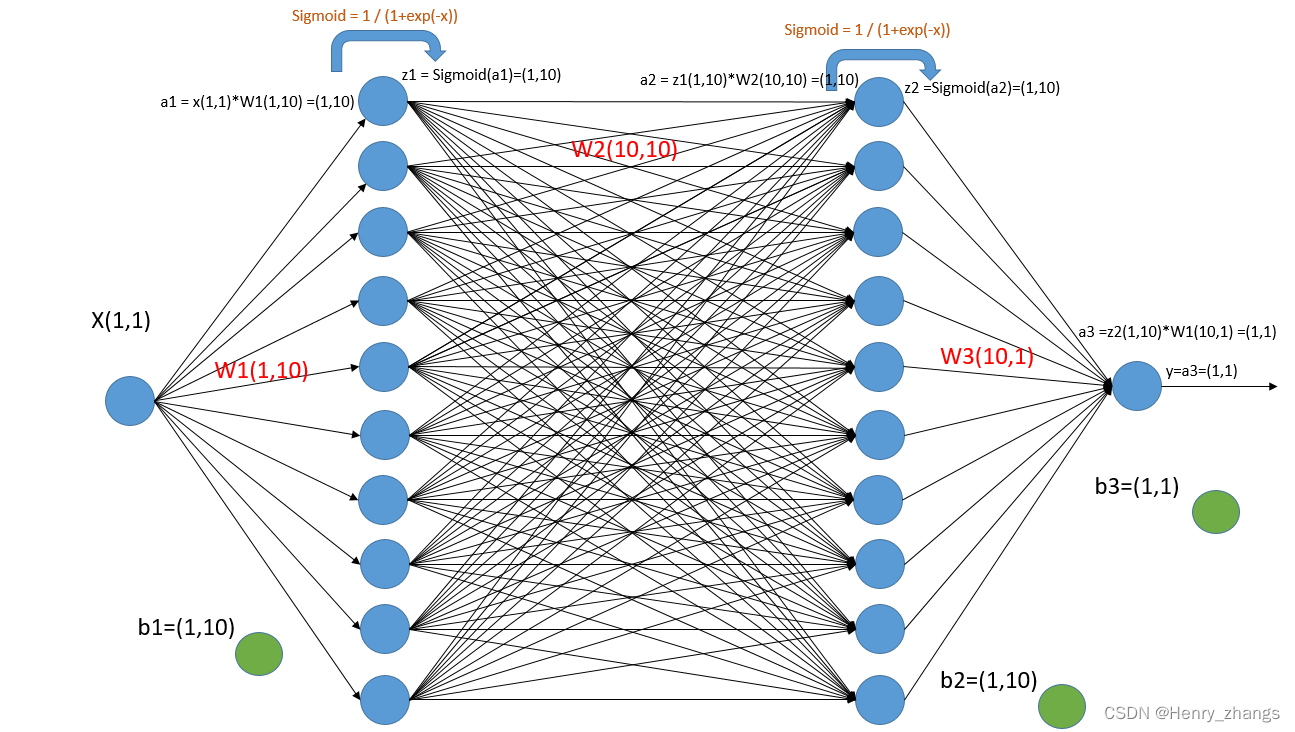
这里实现一个3层的包含两个隐藏层的线性网络(这里的层数是指有实际权重的,也有的是称为4层),其中第一层的节点数为10,第二层也为10,最后一层的输出为1
网络的结构如图:
- 这里采用的激活函数为 sigmoid
- forward和backward的时候,注意每一层的shape
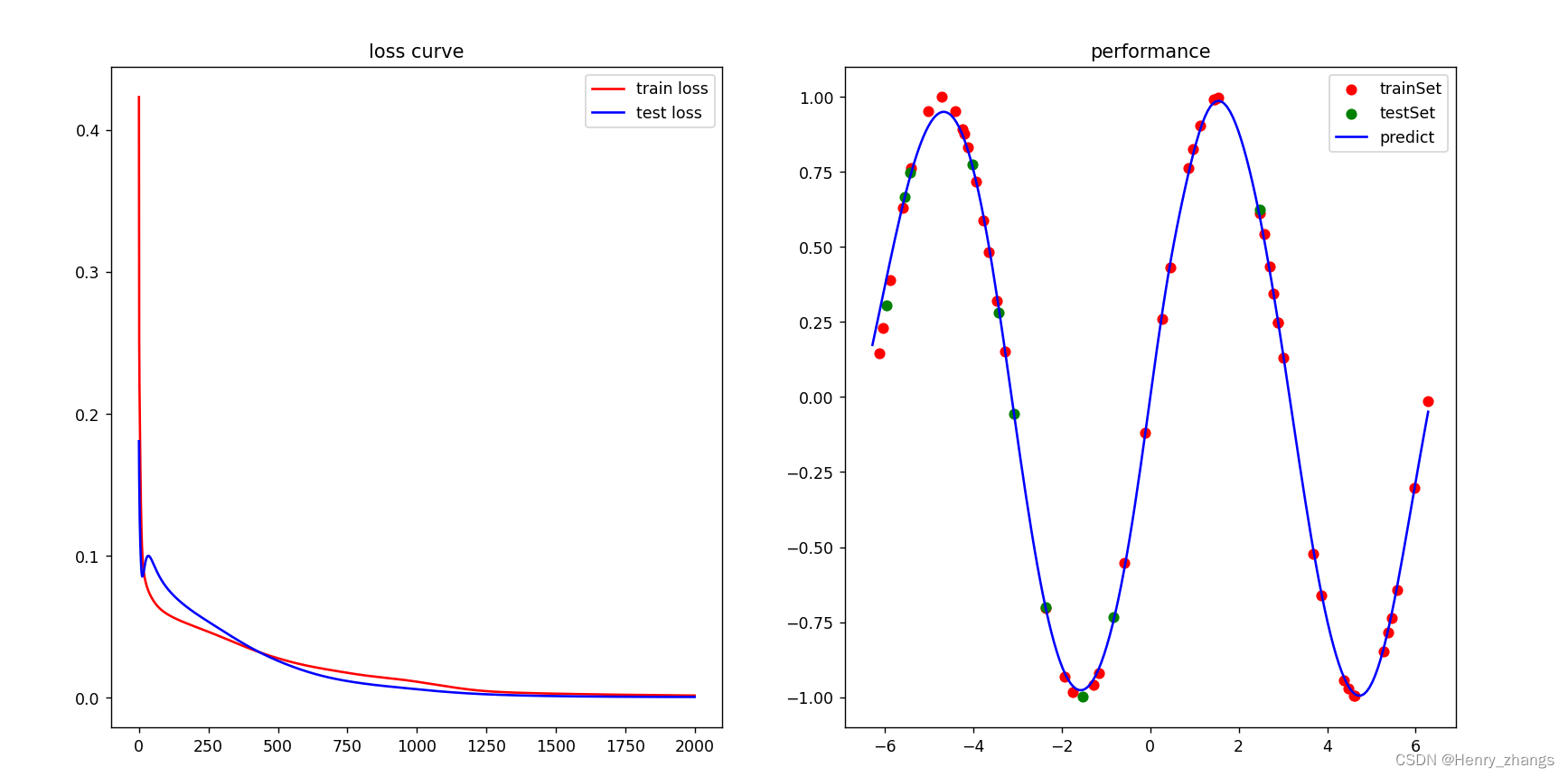
最终实现的效果为:
2. 文件目录
因为用的是pycharm实现的,为了方便,将代码进行模块化
- demo 是train的过程
- model 存放3层线性网络
- utils 是一些工具函数,例如sigmoid、获取sin数据集等等
3. utils 模块
这里主要实现五个功能
前两个是对sigmoid 函数的实现,以及sigmoid函数的求导
sigmoid的导数就是对应的 输出 * (1 - 输出) ,所以sigmoid的反向传播需要网络前向传播*传递的梯度
其次就是损失函数的实现,因为是回归预测的任务,这里采用MSE均方差损失
这里传递的是单个样本,因此loss不需要mean
mse反向的梯度就是预测值 - 真实值
最后就是获取数据集
这里期望的数据范围是 -2pi~2pi之间,random产生的是0.0-1.0之间的浮点数,通过下面的变换就可以得到期望的数据集
这里的shape很重要,因为定义的网络输入是单个神经元,因此要保证数据是(n,1)的
4. 线性网络 + forward + backward
这里全部封装到model里面,因为forward需要sigmoid函数,backward需要对应的梯度,所以需要导入定义的utils
class类里面封装三个实现方法,init是定义多层线性网络,forward是网络的预测,backward是反向传播
这里为了搭建更好的模型,将中间隐藏层设定为手动的,为了下面shape的讲解,这里默认为10
4.1 定义线性回归模型
模型如下:
代码如下:
def __init__(self,hidden_neuron_one=10,hidden_neuron_two=10):
self.parameter = {}
self.parameter['W1'] = np.random.randn(1,hidden_neuron_one) # 第一层
self.parameter['b1'] = np.zeros((1,hidden_neuron_one))
self.parameter['W2'] = np.random.randn(hidden_neuron_one, hidden_neuron_two) # 第二层
self.parameter['b2'] = np.zeros((1,hidden_neuron_two))
self.parameter['W3'] = np.random.randn(hidden_neuron_two,1) # 第三层
self.parameter['b3'] = np.zeros((1,1))
# 生成层
self.layers = {}
self.layers['fc1'] = [self.parameter['W1'],self.parameter['b1']]
self.layers['fc2'] = [self.parameter['W2'],self.parameter['b2']]
self.layers['fc3'] = [self.parameter['W3'],self.parameter['b3']]
# 保存forward里面的值
self.out = []定义参数字典,将每层的参数传递进去,需要注意的是参数的shape,要和定义的一样
最后将同一层的weight和bias放到同一层里面
self.out 帮助我们获取某些特定层网络的输出,因为例如sigmoid的梯度需要前向传播的值,需要将这些值保存,帮助backward
4.2 前向传播
代码如下:
def forward(self,x):
W1,W2,W3= self.parameter['W1'],self.parameter['W2'],self.parameter['W3']
b1,b2,b3= self.parameter['b1'],self.parameter['b2'],self.parameter['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1) # 第一个隐藏层输出
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2) # 第二个隐藏层输出
a3 = np.dot(z2, W3) + b3
y = a3 # 第三个输出
self.out.append(x) # 1*1
self.out.append(z1) # 1*10
self.out.append(z2) # 1*10
return y这里也比较简单,就是对应的矩阵乘法,这里需要将每一层的输出保存下,为了反向传播使用
4.3 反向传播
反向传播的实现较为复杂
这里backward 需要传递的参数有三个
网络最终的输出值y,对应的label,以及学习率
反向传播的关键是矩阵的乘法,以及反向传递的维度要和前向传播的一致
4.3.1 loss 的梯度
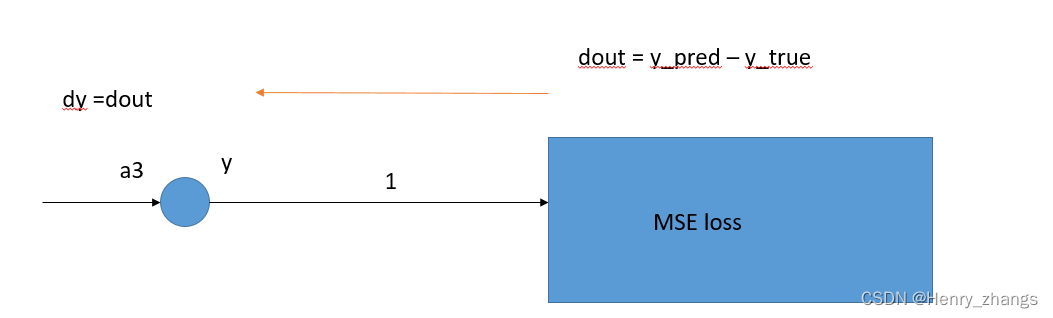
因为loss是mse损失,所以loss的梯度就是y_pred - y_true,这里调用utils定义的loss的梯度(好像没必要,之间减好像更简单....)
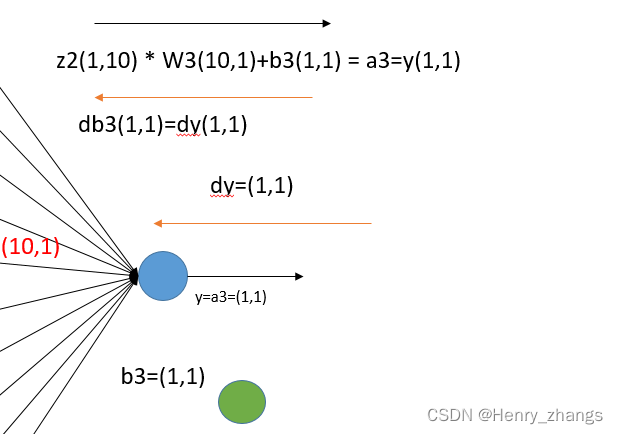
所以当反向传递的梯度流到a3的时候,和dout(图中的dloss)是一样的
记住,因为loss是标量,因此反向传递的shape是1*1的
注:反向的维度是矩阵的形式,是因为我们定义数据的时候,返回的就是二维矩阵(n,1)
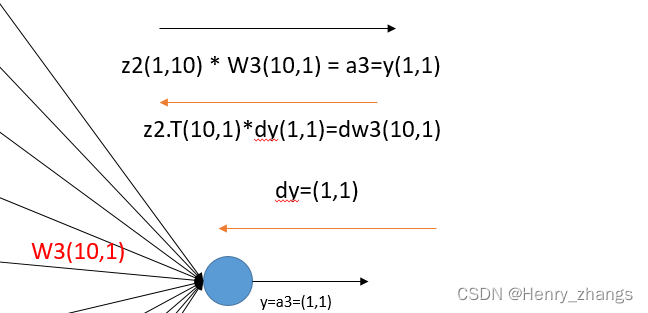
4.3.2 对 W3 的反向传播
矩阵的反向传播可以参考这个: 聊聊关于矩阵反向传播的梯度计算
得出的结论就是:计算谁的时候,就用反向传递的值替换掉谁,然后将另一个元素转置,顺序不变
例如:因此这里的反向传播过来的dw3维度是和W3对应的!!!!!
注:x*w = y或者w*x=y 没关系,只要满足矩阵相乘就行了
同理,这里bias的梯度也可以得到
所以这里代码实现为:
dw3 = np.matmul(self.out[-1].T,dy) # dw3 = z2.T * dy = 10*1
db3 = dy # db3 :1*1 就是上游传递过来的梯度
4.3.3 对 W2 的反向传播
因为想再往前传播的话,这里的dw3和db3就没用了,它们在等着梯度下降了
那么怎么将梯度传递回去呢?
现在目标是将dy传递的梯度传给z2,dw3是不能用的,这个地方的梯度到这就截止了。
那么回想前向传播的公式:z2(1,10) * W3(10,1)+b3(1,1) = a3=y(1,1),只需要将梯度传递给z2的话,通过矩阵反向传播就是:dy(1,1) * W3.T(1,10) =dz2(1,10) 和 z2的维度是匹配的
然后经过sigmoid的梯度,反向流动的梯度就可以到a2
同理计算dw2 的话,就是先看前向传播是:z1(1,10) * W2(10,10) + b2(1,10) = a2(1,10)
反向的话,替换+转置即可:dw2 = z1.T(10,1) * da2(1,10) = (10,10), db2 = da2(1,10)
维度同样是匹配的!!!
dz2 = np.matmul(dy, self.layers['fc3'][0].T) # dz2 = dy * W3.T = 1*10
da2 = dz2 * d_sigmoid(self.out[-1]) # da2 = dz2 对 sigmoid 求导 = 1*10
dw2 = np.matmul(self.out[-2].T, da2) # dw2 = z1.T * da2 = 10*10
db2 = da2 # db2 : da2 就是da2的梯度 = 1*10
这里out列表存放的是:
4.3.4 对 W1 的反向传播
道理是一样的,这里不再赘述了
dz1 = np.matmul(da2, self.layers['fc2'][0].T) # dz1 = da2 * W2.T = 1*10
da1 = dz1 * d_sigmoid(self.out[-2]) # da1 = dz1 对 sigmoid 求导 = 1*10
dw1 = np.matmul(self.out[-3].T, da1) # dw1 = x.T * da1 = 1*10
db1 = da1 # db1 : da2 就是 da1的梯度 = 1*10
4.3.5 梯度下降
梯度下降的部分:
self.layers['fc1'][0] -= lr * dw1
self.layers['fc1'][1] -= lr * db1
self.layers['fc2'][0] -= lr * dw2
self.layers['fc2'][1] -= lr * db2
self.layers['fc3'][0] -= lr * dw3
self.layers['fc3'][1] -= lr * db3
5. train 训练
训练的过程都一样的,为了方便代码的调试,将超参数放到前面
完整的代码在后面
6. 训练结果+可视化
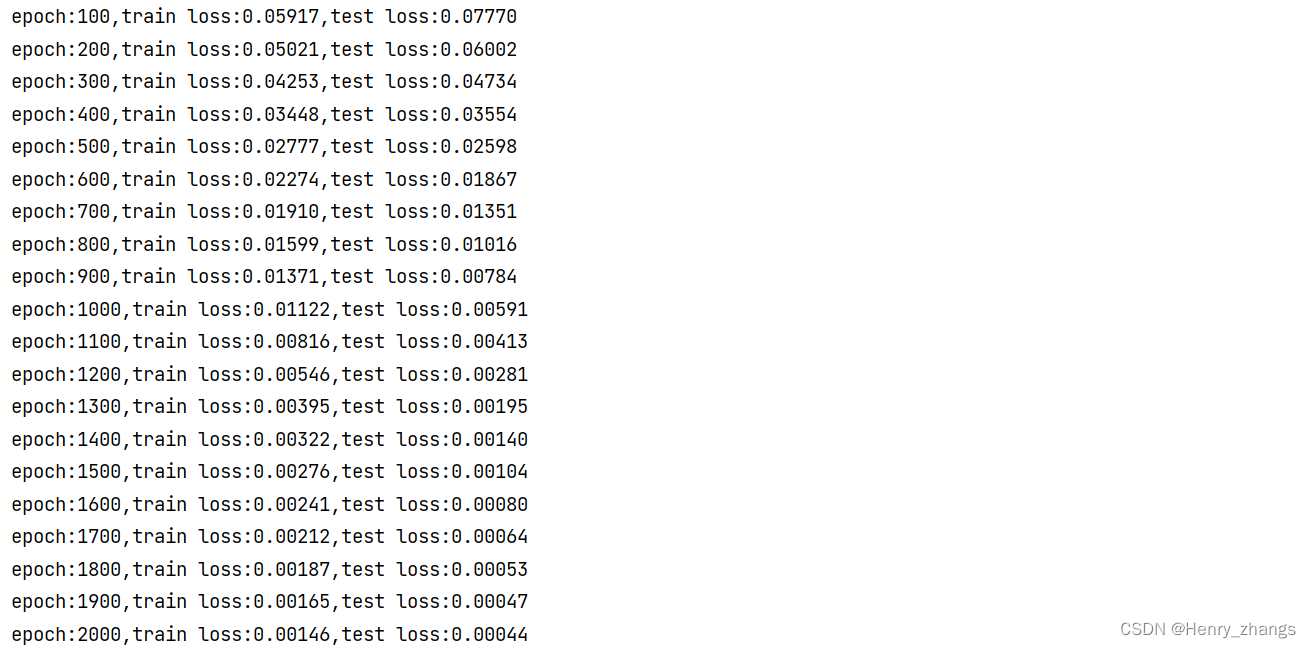
训练过程
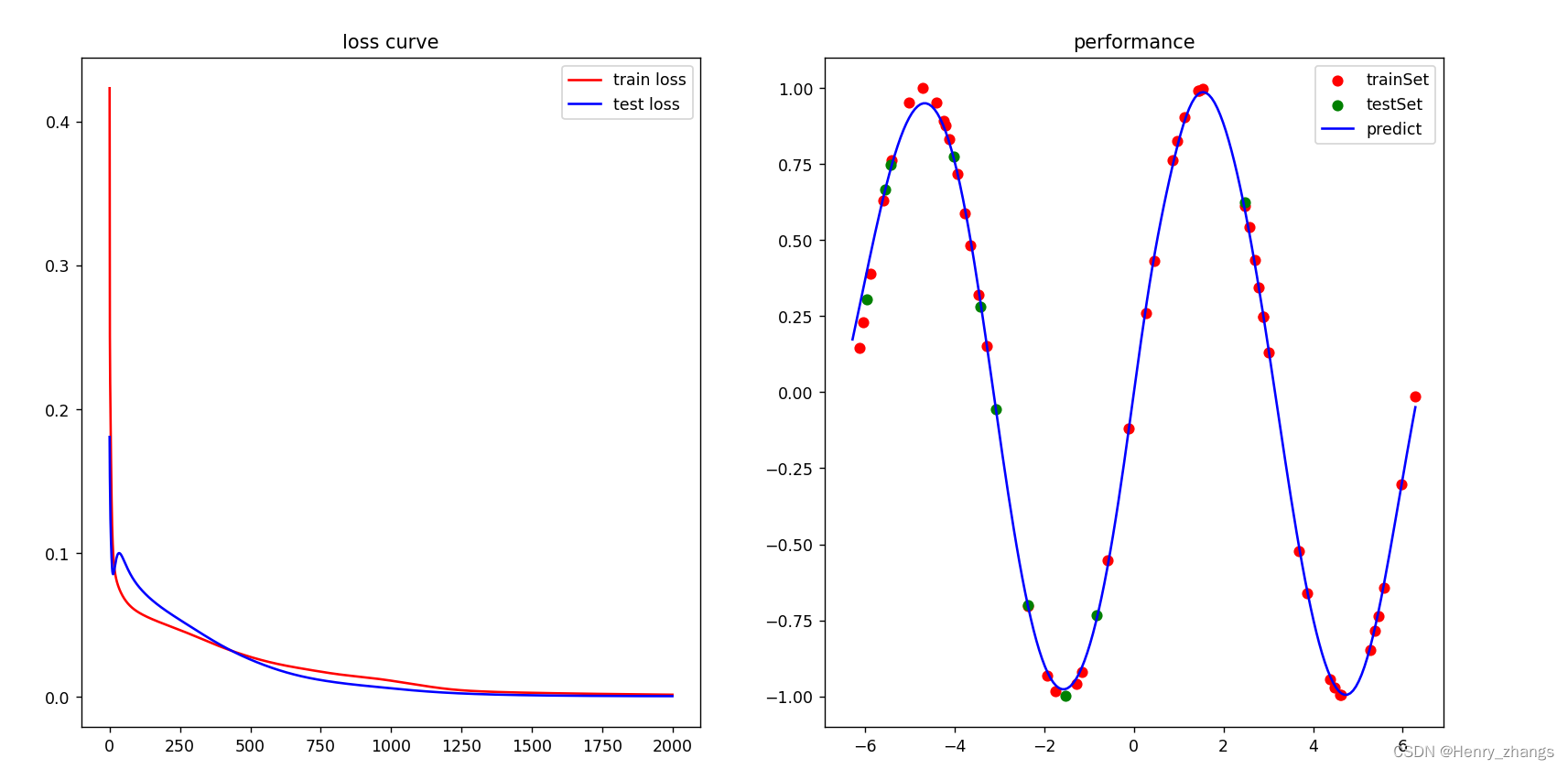
结果展示:
7. 完整代码
训练部分
import numpy as np
import matplotlib.pyplot as plt
from model import LinearRegression
from utils import get_dataset,mse_loss
# 保证np生成随机数一样
np.random.seed(0)
# 定义超参数
number = 50
test_number = number // 5 # 自动设置 0.2 的测试集
learning_rate = 0.1
epochs = 2000
HIDDEN_NEURON_ONE = 10 # 网络隐藏节点的个数
HIDDEN_NEURON_TWO = 10 # 网络隐藏节点的个数
# 建立神经网络
model = LinearRegression(hidden_neuron_one=HIDDEN_NEURON_ONE,hidden_neuron_two=HIDDEN_NEURON_TWO)
trainSet, trainLabel = get_dataset(number) # 获取训练数据
testSet,testLabel = get_dataset(test_number) # 获取测试数据
epoch_train_loss = []
epoch_test_loss = []
for i in range(epochs):
train_running_loss = 0.0
for x,y in zip(trainSet, trainLabel):
prediction = model.forward(x) # forward
loss = mse_loss(prediction,y) # loss
model.backward(prediction,y,lr=learning_rate) # backward
train_running_loss += loss.item()
test_running_loss = 0.0
for x,y in zip(testSet,testLabel):
prediction = model.forward(x)
loss = mse_loss(prediction,y)
test_running_loss += loss.item()
train_running_loss = train_running_loss / number # loss = loss_sum / 样本个数
test_running_loss = test_running_loss / test_number
epoch_train_loss.append(train_running_loss)
epoch_test_loss.append(test_running_loss)
if (i + 1) % 100 == 0:
print('epoch:%d,train loss:%.5f,test loss:%.5f' % (i + 1, train_running_loss, test_running_loss))
plt.figure(figsize=(12,8))
plt.subplot(1,2,1),plt.title('loss curve')
plt.plot(epoch_train_loss,label = 'train loss',color='r') # 训练损失
plt.plot(epoch_test_loss,label = 'test loss',color = 'b') # 测试损失
plt.legend()
axis_x = np.linspace(-2*np.pi,2*np.pi,200).reshape(-1,1)
out = model.forward(axis_x)
plt.subplot(1,2,2),plt.title('performance')
plt.scatter(trainSet,trainLabel,label='trainSet',color='r') # 训练样本
plt.scatter(testSet,testLabel,label='testSet',color='g') # 测试样本
plt.plot(axis_x,out,label='predict',color = 'b')
plt.legend()
plt.show()
定义网络部分
import numpy as np
from utils import sigmoid,d_sigmoid,d_mse_loss
# 线性回归
class LinearRegression:
def __init__(self,hidden_neuron_one=10,hidden_neuron_two=10):
self.parameter = {}
self.parameter['W1'] = np.random.randn(1,hidden_neuron_one) # 第一层
self.parameter['b1'] = np.zeros((1,hidden_neuron_one))
self.parameter['W2'] = np.random.randn(hidden_neuron_one, hidden_neuron_two) # 第二层
self.parameter['b2'] = np.zeros((1,hidden_neuron_two))
self.parameter['W3'] = np.random.randn(hidden_neuron_two,1) # 第三层
self.parameter['b3'] = np.zeros((1,1))
# 生成层
self.layers = {}
self.layers['fc1'] = [self.parameter['W1'],self.parameter['b1']]
self.layers['fc2'] = [self.parameter['W2'],self.parameter['b2']]
self.layers['fc3'] = [self.parameter['W3'],self.parameter['b3']]
# 保存forward里面的值
self.out = []
def forward(self,x):
W1,W2,W3= self.parameter['W1'],self.parameter['W2'],self.parameter['W3']
b1,b2,b3= self.parameter['b1'],self.parameter['b2'],self.parameter['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1) # 第一个隐藏层输出
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2) # 第二个隐藏层输出
a3 = np.dot(z2, W3) + b3
y = a3 # 第三个输出
self.out.append(x) # 1*1
self.out.append(z1) # 1*10
self.out.append(z2) # 1*10
return y
def backward(self,predict,label,lr):
dout = d_mse_loss(predict,label) # 对 loss的梯度 1*1
dy = dout * 1 # 梯度流到 y(a3) 1*1
dw3 = np.matmul(self.out[-1].T,dy) # dw3 = z2.T * dy = 10*1
db3 = dy # db3 :1*1 就是上游传递过来的梯度
dz2 = np.matmul(dy, self.layers['fc3'][0].T) # dz2 = dy * W3.T = 1*10
da2 = dz2 * d_sigmoid(self.out[-1]) # da2 = dz2 对 sigmoid 求导 = 1*10
dw2 = np.matmul(self.out[-2].T, da2) # dw2 = z1.T * da2 = 10*10
db2 = da2 # db2 : da2 就是da2的梯度 = 1*10
dz1 = np.matmul(da2, self.layers['fc2'][0].T) # dz1 = da2 * W2.T = 1*10
da1 = dz1 * d_sigmoid(self.out[-2]) # da1 = dz1 对 sigmoid 求导 = 1*10
dw1 = np.matmul(self.out[-3].T, da1) # dw1 = x.T * da1 = 1*10
db1 = da1 # db1 : da2 就是 da1的梯度 = 1*10
self.layers['fc1'][0] -= lr * dw1
self.layers['fc1'][1] -= lr * db1
self.layers['fc2'][0] -= lr * dw2
self.layers['fc2'][1] -= lr * db2
self.layers['fc3'][0] -= lr * dw3
self.layers['fc3'][1] -= lr * db3
工具函数utils
import numpy as np
# sigmoid
def sigmoid(x):
y = 1 / (1+np.exp(-x))
return y
# sigmoid 梯度
def d_sigmoid(x):
y = x*(1-x)
return y
# mse 损失
def mse_loss(predict,label):
loss = 0.5*(predict - label) ** 2
return loss
# loss 的梯度
def d_mse_loss(predict,label):
y = predict - label
return y
# 获取数据集
def get_dataset(num):
data_x = np.random.random((num,1)) * np.pi * 4 - np.pi * 2 # 返回 -2pi~2pi 随机值
data_x = data_x.reshape(-1,1)
data_y=np.sin(data_x).reshape(-1,1)
return data_x,data_y
8. 其它
这里用的是单个样本的下降,也就是SGD,因为SGD虽然收敛的速度慢,但是单个样本的噪声对推动饱和区的loss也是有帮助的
之前忘记在哪里见过的,线性网络是没有局部最优的,不知道是不是记错了。
saddle point 概率很小,因为要满足的条件很苛刻才能出现(hessian矩阵)
然后就是,这里没有涉及 mini batch 的实现。
可以尝试一下这样 for i in range(batch_size) ,将这些的pred和label求均值,这样可以简单实现batch 的输入。因为batch的size越大,理论上可以更加反应整个样本的概率分布,这样网络就更能对这样同分布样本进行预测。