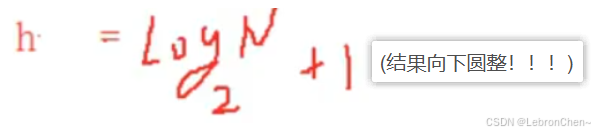一.时间/空间复杂度
1.算法的时间复杂度为算法中基本操作的执行次数(渐进执行次数)。
2.冒泡排序的(时间复杂度/执行次数)为:1+2+3+...+(n-1)=n^2/2-n/2;其最优时间复杂度/渐进执行次数为:O(n^2),其平均时间复杂度/渐进执行次数为:O(n^2/2),其最差时间复杂度/渐进执行次数为:O(n)。
| 实际执行次数如何转换成时间复杂度(渐进执行次数) | |
| 执行次数: | 渐进执行次数: |
| n^2+2n+10 | O(n^2)[2n+10对n^2影响不大] |
| 2n^2+8n+5 | O(n^2)[2倍对n^2影响不大] |
| m+n | O(m+n)[除非已知m远大于n,不然不能忽略任何一个] |
| 100 | O(1)[常数的渐进执行次数为1] |
3.空间复杂度与时间复杂度计算执行次数思路相同。
二.顺序表与链表
顺序表(数组)与链表的区别和联系:
1.
2.
3.单链表
4.异或的概念:相同为0,相异为1.
5.链表有8种结构
三.栈和队列
1.栈的概念及结构(一般使用数组表达)
(一个入栈队列根据出栈顺序对应多个出栈队列,但每个出栈队列都有一个原则,即大数后的小数都是有序或间隔有序排列的,如先出了大数4,则4后的123这三个数,只能按321或32或21或31来出,不能出现213的情况)
1.队列的概念及结构(一般使用单链表表达)
(一个入队列有且对应一个出队列)
四.二叉树
1. 树的相关概念
2. 树的表示
3. 二叉树的特点
3.1
3.2完全二叉树的叶子节点的个数=(完全二叉树节点的个数+1)/2 (结果向下圆整!!!)
3.3二叉树共有N个节点,其高度为h。
若为满二叉树时,其高度为:
若为完全二叉树时,其高度为
3.4二叉树下标特点
3.5完全二叉树(内含满二叉树)一般都用顺序表(数组)来表示
3.6二叉树遍历方式
前序(根左右)
中序(左根右)
后序(左右根)
层序(根据层数从左到右遍历)
4. 堆的特点
4.1大堆小堆的概念
下文以小堆举例,大堆道理一样!
a.AdjustDown(int* a, int n, int root)-------------------AdjustDown向下调整法
从根root开始的向下调整法可以将除根外左右子树都为小堆的无序堆调整为小堆;时间复杂度为:O(logN)
b.AdjustDown(int* a, int n, int (end-1)/2)----------AdjustDown向下调整法
从末节点end的父节点(end-1)/2开始的向下调整法可以将毫无规律的无序堆调整为小堆;时间复杂度为:O(N)
4.2堆排序时若升序排则建大堆,降序排则建小堆
4.3若有N个数,要找到其中最大的前K个数,则是先对该无序数组的头K个数建小堆,再将后(K+1)~N个数依次和小堆 堆顶的数进行比较,若比小堆 堆顶的数大,则将其覆盖掉小堆 堆顶的数(这里不用Swap交换,因为被覆盖掉的小堆 堆顶的数没用了),再将更新堆顶值后的新堆进行向下调整法构件成新的小堆,从而达到将不在头K个数中的最大的前K个数替换到头K个数中,继而往复遍历比较到第N个数,即可将N个数中最大的前K个数都替换到头K个数中来,再输出头K个数即可。
五.排序
排序种类:
注:这篇笔记中的部分图片来源于比特鹏哥的视频(超级感谢鹏哥!)