【ACL 2023】A Novel Table-to-Graph Generation Approach for Document-Level Joint Entity and RE

【ACL 2023】A Novel Table-to-Graph Generation Approach for Document-Level Joint Entity and Relation Extraction

论文：https://aclanthology.org/2023.acl-long.607/

代码：https://github.com/ridiculouz/TaG / https://github.com/tonytan48/Re-DocRED

Abstract

文档级关系提取（DocRE）旨在提取文档中实体之间的关系，这对知识图构建等应用程序至关重要。现有的方法通常假设实体及其提及是预先识别的，这与现实世界中的应用程序不符。为了克服这一限制，我们提出了TAG，这是一种新的 table-to-graph 生成模型，用于在文档级别联合提取实体和关系。为了增强任务依赖性的学习，TAG在提及之间引入一个潜在图，不同类型的边指示不同的任务信息，并通过关系图卷积网络进一步传播。为了缓解错误传播问题，我们采用分层聚集聚类算法在解码阶段反向传播任务信息。在基准数据集DocRED上的实验表明，TAG在很大程度上超过了以前的方法，并取得了最先进的结果。

Introduction

早期的研究主要集中在句子层面的Relation Extraction（RE），即在一个句子中预测实体之间的关系。然而，在维基百科文章或科学论文等现实世界场景中，大量的关系事实是在多个句子中表达的，这就需要句子间推理技巧。因此，最近的努力一直在向更现实的文档级RE（DocRE）迈进。

尽管进展迅速，但大多数以前的DocRE方法都只专注于关系提取任务，该任务假设实体及其相应的提及是预先给定的。如图1所示，要在文档级别提取实体和关系，自然的想法是使用pipline方法。传统上，它首先将整个任务划分为提及提取（ME）、共指消解（COREF）和关系提取（RE）的子任务，然后使用单独的模型逐步执行每个任务。然而，流水线框架忽略了子任务之间的底层依赖关系，这可能导致性能不理想。在联合考虑子任务方面已经取得了一些进展，然而，之前的尝试仍然分别对COREF和RE的任务进行建模，在编码和解码阶段都可能产生偏差。一方面，这些方法仍然存在缺乏信息共享的问题。它们要么完全依赖于共享语言模型（例如BERT），或者只考虑从RE到COREF的单向信息流，而忽略其他跨任务依赖性。另一方面，现有的方法大多采用流水线式解码，首先识别提及跨度并形成实体簇，然后对每个实体对进行关系分类。这样的例程不仅耗时，而且还面临着错误传播问题。实体提取的结果可能会影响关系提取的性能，并导致级联错误。Xu和Choi试图在COREF得分手中使用正则化术语来缓解这个问题，但这个问题仍然没有完全解决。

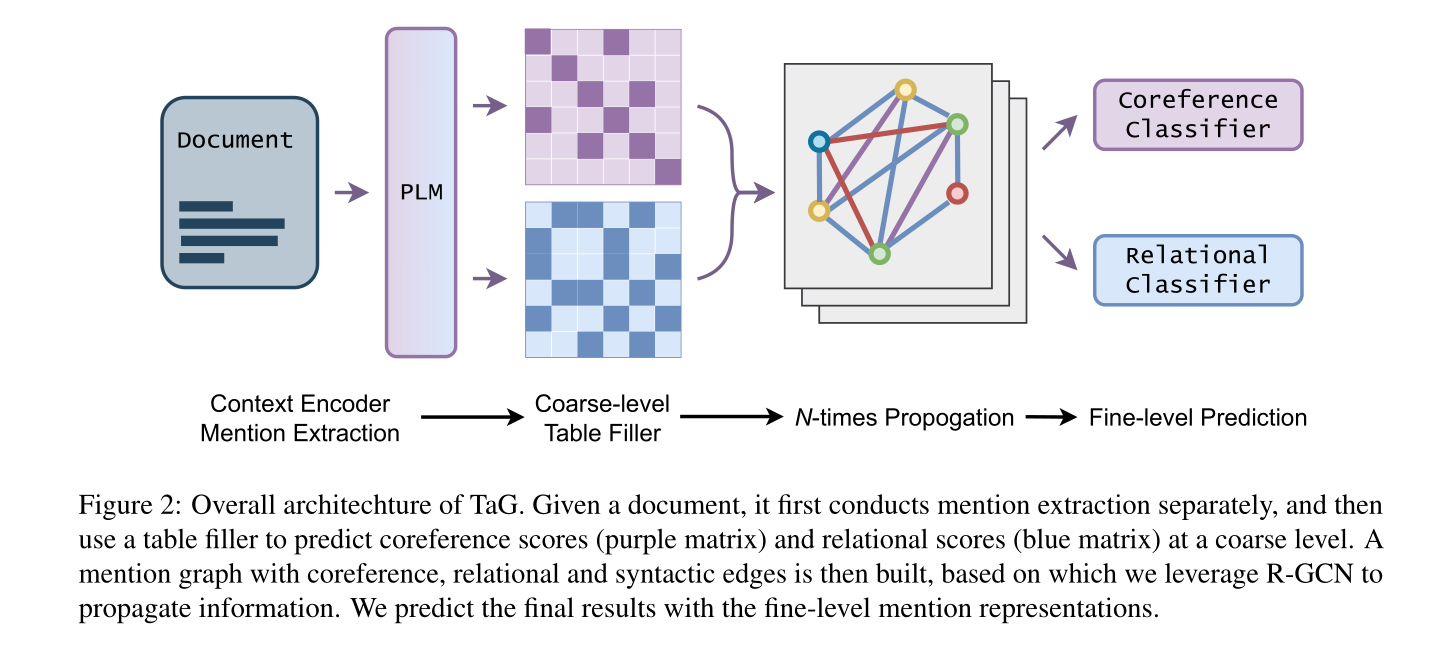
在这项工作中，我们提出了TAG，一种新的 table-to-graph 生成模型，以解决上述挑战。我们首先将COREF和RE的任务与经典的表填充框架统一起来。然后，我们设计了一个下面的表格填充器来对原始文本进行编码，并对这两项任务进行粗略的预测。将提及作为节点，我们动态地构建两个相应的共指图和关系图，其中边由表填充器的置信度得分加权。此外，为了缓解长期依赖问题，并对句法信息进行显式建模，我们构建了一个过度提及的句法图。给定这三个子图，TAG将它们视为三种不同类型的边，并使用关系图卷积网络（RGCN）对隐式任务依赖性进行精细建模。与以前仅直接从语言模型共享跨度表示的多任务系统不同，我们的粗到细框架通过语义和句法链接传播信息，利用丰富的节点表示。

直观地说，同一实体集群中的提及应该与其他实体建立类似的关系链接。为了避免错误传播问题，我们利用这一假设，并将层次聚集聚类（HAC）算法应用于聚类提及。HAC的核心是计算每个聚类对之间的共指距离。为了反向传播关系信息，我们计算节点的关系向量，并使用不同集群之间的平均汉明距离（Hamming distance）作为额外的惩罚。

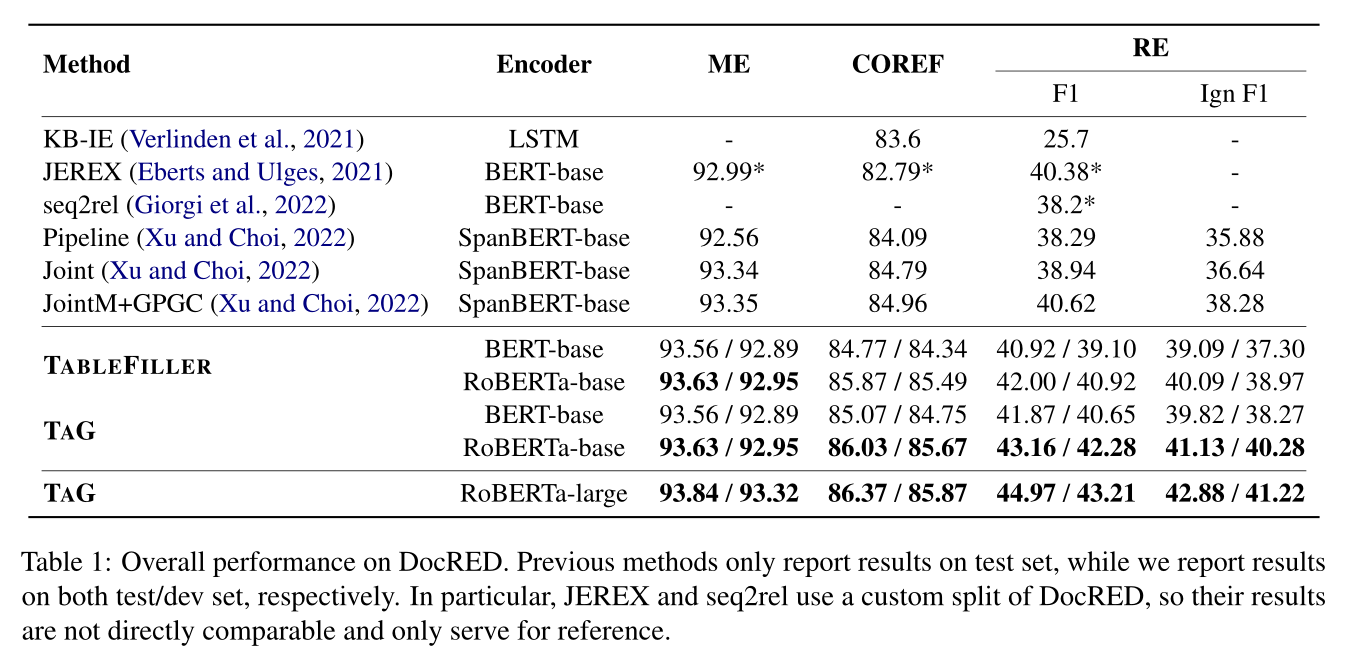
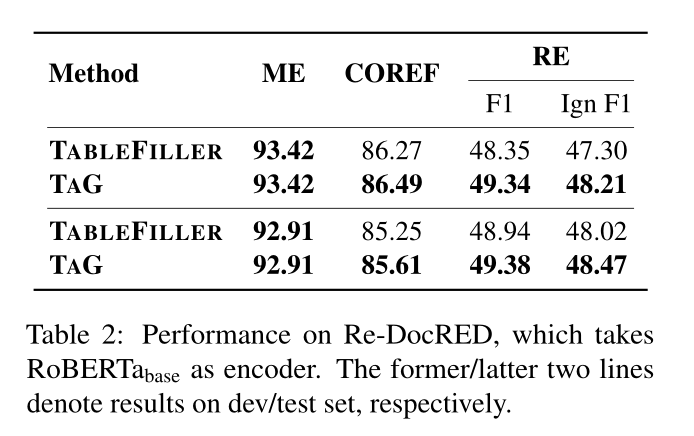
我们在DocRED数据集上评估TAG，这是一个广泛采用的DocRE基准。实验表明：（1）与以前的方法相比，粗粒度的表填充基线建立了具有竞争力的结果。（2）细粒度的信息传播模块和增强的HAC解码算法可以有效地促进跨任务交互，更好地缓解错误传播问题。（3）我们提出的TAG实现了新的最先进技术，并在很大程度上优于先前的方法。我们还报告了关于Re-DocRED的联合实体和关系提取的第一个结果，这是DocRED的修订版，用于未来的研究。

我们的贡献可以总结如下：

我们将COREF和RE在文档级联合实体和关系提取中的任务与表填充框架相统一，并提出了一种新的 table-to-graph 生成方法TAG，以促进信息共享。在解码阶段，我们采用HAC算法来增强RE预测的COREF，从而减轻错误传播的问题。
我们证明TAG超越了以前的方法，并在标准DocRE基准上获得了最先进的新结果。

Problem Formulation

给定由 $L$ 个token组成的文档 $D$ ，我们的目标是以端到端的方式联合抽取所有实体和关系。由于一个实体可能在文档中多次出现，并有不同的提及，因此联合提取过程可以自然地分为三个子任务：

提及提取（ME），它提取所有可能的跨度 $\mathcal{M}=\{m_i\}^M_{i=1}$ 表示原始文档中的实体，其中跨度定义为单词的连续序列；
共指解析（COREF），将本地提及分组为实体簇 $\mathcal{E}=\{e_i\}^E_{i=1}$ ，其中 $e_i=\{m^i_j\}^{N_{e_i}}_{j=1}$ ;
关系提取（RE），它从实体对 $(e_h,e_t)_{h,t=1,\dots,E;h \ne t}$ 之间的预定义关系集 $\mathcal{R} \cup {\bot}$ ， $\bot$ 表示没有关系。

与以往的工作不同，我们使用表格填充框架来制定COREF和RE的任务，每个提及对 $m_i,m_j)$ 之间的多类分类。我们维护一个表 $T^{|M|\times|M|}$ 来表示提及对，并对这两个任务使用共享表示。

我们分别为表中的每个单元分配COREF标签 $y_c^{(i,j)} \in \{ 0,1\}$ 和RE标签 $y_r^{(i,j)} \subseteq \mathcal{R} \cup \{\bot \}$ 。对于COREF，我们使用1/0来表示提及对是否属于同一实体。对于RE，我们将实体级标签转移到提及级，其中提及对 $m_i,m_j)$ 标记有其所属实体 $e_h,e_t)$ 的相同关系，其中 $m_i \in e_h,m_j \in e_t$ 。

Methodology

Mention Extractor

我们将实体提及提取问题归结为具有BIO标记的序列标记任务。尽管基于跨度的方法由于其更强的表达能力而更为普遍，但它们通常需要 $\mathcal{O}(L^2)$ 时间复杂性，而基于序列的方法只需要线性时间。由于DocRE的任务包含很少的重叠点，为了提高效率，我们采用了顺序方法。

我们利用预训练语言模型（PLM）将文档中的token转换为矢量化特征，并使用分类器预测每个标记的BIO标签。我们将提取的提及表示为 $\{m_i\}^M_{i=1}$ 。

Table-to-Graph Generation

Biaffine Table Filler

给出一个文档 $D=[w_i]_{i=1}^L$ 和提及 ${m_i \}_{i=1}^M$ ，我们构建了每个提及对的表表示。我们采用实体标记策略，在每次提及的开始和结束处插入一个特殊的标记“”。然后，我们使用单独的PLM来获得上下文表示 ${H}=[\mathbf{h}_1,\dots,\mathbf{h}_L]^{\tau}$ ， $\mathbf{h}_i\in \mathbb{R}^d$ 和多头注意力 $\mathbf{A}\in \mathbb{R}^{H\times L \times L}$ ：
$\mathbf{H,A}=\text{PLM}([w_1,\dots,w_L])$
其中 $\mathbf{A}$ 是最后一个transformer层中的多头注意力矩阵。我们将起始标记“”的嵌入视为提及的嵌入。为了捕获相关的上下文对 $m_i,m_j)$ ，我们应用本地化上下文池技术来计算上下文嵌入 $c^{(i,j)}$ ：
$q^{(i,j)}=\sum_{k=1}^H \mathbf{A}_k^i \circ \mathbf{A}_k^j,\\ c^{(i,j)}=\mathbf{H}^{\top} \frac{q^{(i,j)}}{1^{\top} q^{(i,j)}}$
$\circ$ 是指Hadamard乘积， $\mathbf{A}_k^i, \mathbf{A}_k^j \in \mathbb{R}^L$ 分别是 $m_i,m_j$ 在第 $k$ 个注意力头中的注意力权重。 $c^{(i,j)}$ 是从对 $m_i$ 和 $m_j$ 都高度关注的token聚合而来的，因此可能对它们都很重要。

让 $h_i,h_j$ 成为PLM中 $m_i,m_j$ 的隐藏特征。我们首先将 $h_i,h_j$ 和 $c^{(i,j)}$ 投影为头部和尾部特征:
$z_i^{(i,j)}=\tanh(W_h h_i + W_{ch} c^{(i,j)}),\\ z_j^{(i,j)}=\tanh(W_t h_j + W_{ct} c^{(i,j)})$
$W_h,W_{ch},W_t,W_{ct} \in \mathbb{R}^{d \times d}$ 是可训练的参数。然后，我们使用biaffine注意力模型将提及特征转换为表示共指或关系链接的标量分数的表 $S\in \mathbb{R}^{M\times M}$ ：
$s^{(i,j)}=z_i^{(i,j)}W_1 z_j^{(i,j)} + w_2^{\top}(z_i^{(i,j)} \oplus z_j^{(i,j)})+b$
$W_1 \in \mathbb{R}^{d \times d},w_2 \in \mathbb{R}^{2d},b \in \mathbb{R}$ 是可训练参数， $\oplus$ 是连接操作。我们分别预测具有共享表示 $z$ 的共指和关系得分 $S_{tc},S_{tr}$ 。特别地，如果RE标签 $y_r^{(i,j)} \ne \{ \bot \}$ ，则 $s_{tr}^{(i,j)}$ 被标记为1，否则为0。

Latent Graph Construction

共指图和关系图。在获得共指和关系得分 $S_{tc},S_{tr}$ 之后，我们针对列对每个表进行归一化：
$G_c=\text{Softmax}(S_{tc}),\\ G_r=\text{Softmax}(S_{tr})$
我们将 $G_c$ 和 $G_r$ 作为先前模块预测的共指和关系链接的动态加权图。每个单元 $g^{(i,j)}$ 表示有向边 $m_i \to m_j$ 的权重。

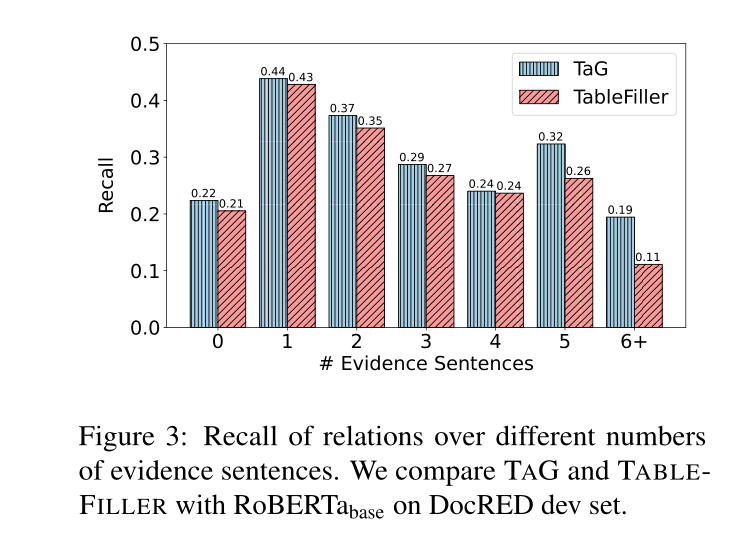
句法图。为了增强对自然语言基础结构知识的学习，我们试图在提及图中显式地引入句法信息。理想情况下，句法链接可以有效地编码本地上下文，这些上下文可以通过共同引用或关系链接进一步广播。因此，它使模型能够在良好的水平上学习长期依赖关系。

有几种可选的方法可以构建所需的语法图。例如，一个直观的解决方案是将单词上的依赖树转移到图中，其中提及是节点。由于依赖树只揭示句内线索，以前的工作通常会利用共现信息。按照这种做法，我们的句法图 $G_s$ 使用双向边连接同一句子中的所有提及。

Propagating Information with R-GCN

为了考虑COREF和RE任务之间的相互作用，并结合明确的语法信息，我们提出了一个信息传播模块来细化提及表示。

具体地，我们将潜在图 $G_c,G_r,G_s$ 视为提及图上的三种不同类型的边。然后，我们在提到的图上应用关系图卷积网络来聚合沿不同类型边的邻居特征。给定第 $l$ 层的节点 $x_i$ ，更新过程由
$x_i^{(l+1)}=\tanh(\sum_{t \in \{ c,r,s\}}\sum_{j=1}^M g_t^{(i,j)}W_t^l x_j^l +b_t^l)$
$t$ 是边的类型， $g_t^{(i,j)}$ 表示有向边 $m_i \to m_j$ ， $W_t^l,b_t^l$ 是可训练参数。我们初始化节点嵌入 $x_i^0$ 使用提及 $m_i$ 的隐藏特征 $h_i$ 。

与之前的Joint IE方法不同，前者要么以流水线方式传播任务信息（DYGI），要么只考虑单向信息流，我们的模块并行集成了跨任务信息，并提取了两个任务的相关提及特征。

Classifier

在 $N$ 次传播之后，我们使用强化提及嵌入 $x^N_i,x^N_j$ 和上下文嵌入 $c^{(i,j)}$ 来预测COREF得分 $s^{(i,j)}_{gc}$ 和RE得分 $s^{(i,j)}_{gr}$ ：
$v_i^{(i,j)}=\tanh(U_h x_i^N + U_{ch}c^{(i,j)}),\\ v_j^{(i,j)}=\tanh(U_t x_j^N + U_{ct} c^{(i,j)}),\\ s_{gc}^{(i,j)}=\text{CorefBiaff}(v_i^{(i,j)},v_j^{(i,j)}),\\ s_{gr}^{(i,j)}=\text{ReBiaff}(v_i^{(i,j)},v_j^{(i,j)})$
$U_h,U_{ch},U_t,U_{ct} \in \mathbb{R}^{d \times d}$ 是可训练的参数，n维的biaffine函数被定义为：
$\text{Biaff}(x,y)=xU_1^{\top}y+U_2 (x \oplus y)+b$
$U_1 \in \mathbb{R}^{n \times d \times d},U_2 \in \mathbb{R}^{n \times 2d},b \in \mathbb{R}^{n}$ 是可训练参数，注意，对于COREF的任务， $n = 1$ ，对于RE， $n=|\mathcal{R}|+1$ ，其中我们使用伪类TH来学习多标签分类的动态阈值（Zhou等人，2021）。在测试时，分数高于TH类的关系类型被预测为输出 $\hat{y}_r^{(i,j)}$ 。在不存在此类的情况下，分类器返回 $\{ \bot \}$ 。

Training

Table Encoder. 给定提及对 $m_i,m_j)$ ，表编码器以标量分数 $s_{tc}^{(i,j)},s_{tr}^{(i,j)}$ 的形式预测共指和关系链接。对于共引用链接，我们直接使用COREF标签 $y_{c}^{(i,j)}$ 作为正确标注。对于关系链接，我们定义 $y_{rbinary}^{(i,j)}=1(y_{r}^{(i,j)} \ne \{\bot \})$ ，表示是否存在任何关系 $e_h,r,e_t)$ ，其中 $m_i \in e_h,m_j \in e_t$ 。我们用sigmoid函数σ将 $S_c,S_r$ 转换为概率，并用二分类交叉熵损失 $L_{tc},L_{tr}$ 进行优化。

Coreference Resolution. 精细级共指解析的训练目标和标签与表编码器中的共指链接预测的训练目标相同。唯一的区别在于，它采用了强化的提及表示作为输入。我们将损失表示为 $L_{gc}$ 。

Relation Extraction. 对于 $m_i,m_j)$ ，我们将关系集 $\mathcal{R}$ 分为两部分：包含关系 $x$ 的正集 $\mathcal{P}$ 存在于 $m_i,m_j)$ 之间，负集 $\mathcal{N}=\mathcal{R−P}$ 。我们应用自适应阈值损失（Zhou et al，2021）来学习RE分类器：
$\begin{aligned} l^{(i, j)}= & -\sum_{x \in \mathcal{P}} \log \left(\frac{\exp \left(s_{x}^{(i, j)}\right)}{\sum_{x^{\prime} \in \mathcal{P} \cup\{\mathrm{TH}\}} \exp \left(s_{x^{\prime}}^{(i, j)}\right)}\right) \\ & -\log \left(\frac{\exp \left(s_{\mathrm{TH}}^{(i, j)}\right)}{\sum_{x^{\prime} \in \mathcal{N} \cup\{\mathrm{TH}\}} \exp \left(s_{x^{\prime}}^{(i, j)}\right)}\right), \end{aligned}$
最终综合所有的损失，最终的损失函数为：
$L=L_{tc}+L_{tr}+\alpha \cdot(L_{gc}+L_{gr})$

Decoding

为了避免流水线解码中固有的错误传播问题，我们旨在设计一种解码算法，使上游任务（COREF）能够有效地利用下游任务信息（RE）。

Entity Cluster Decoding. 我们基于层次聚集聚类（HAC）算法对实体聚类进行解码，如算法1所述。HAC的核心是测量两个聚类 $C_x$ 和 $C_y$ 之间的距离 $D$ 。我们将 $D$ 分解为两部分：共指距离 $D_c$ 和关系距离 $D_r$ 。我们使用平均链接来计算 $D_c$ 为：
$D_c = \frac{1}{|C_x|\cdot |C_y|} \sum_{m_i \in C_x} \sum_{m_j \in C_y}(1-\sigma(s_{gc}^{(i,j)}))$
在训练阶段，如果 $m_i$ 和 $m_j$ 属于同一实体，对于所有 $m_k\in \mathcal{M}$ ，则标注关系 $y_r^{(i,k)}$ 和 $y_r^{(j,k)}$ 是相同的。因此，对于训练良好的模型，同一实体簇内的提及应与其他实体建立类似的关系链接。我们利用这条线索作为COREF和RE之间的联系。预测RE的标签 $\hat y_r^{(i,j)}$ 是 $\mathcal{R}$ 维度的0-1向量，其中每个数字指示一种关系类型的存在。我们定义关系向量 $r_i \in \mathbf{R}^{2M \times |R|}$ 为
$r_i = [\hat y_r^{i,1},\dots,\hat y_r^{(i,M)},\hat y_r^{1,i},\dots,\hat y_r^{(M,i)}]$
我们使用聚类 $C_x,C_y$ 中每个提及对之间的平均Hamming距离作为 $D_r$ ：
$D_{r}=\frac{1}{\left|C_{x}\right|\left|C_{y}\right|} \sum_{m_{i} \in C_{x}} \sum_{m_{j} \in C_{y}} \sigma\left(\operatorname{Hamming}\left(\mathbf{r}_{i}, \mathbf{r}_{j}\right)\right)$
Relation Triple Decoding. 给定两个实体 $e_1$ 和 $e_2$ ，我们预测它们与多数投票机制的关系标签。对于关系式 $x$ ，最终预测由
$\hat{y}_{x}^{\left(e_{1}, e_{2}\right)}=\mathbb{1}\left(\left(\sum_{m_{i} \in e_{1}} \sum_{m_{j} \in e_{2}} \hat{y}_{x}^{(i, j)}\right)>\frac{\left|e_{1}\right| \cdot\left|e_{2}\right|}{2}\right)$

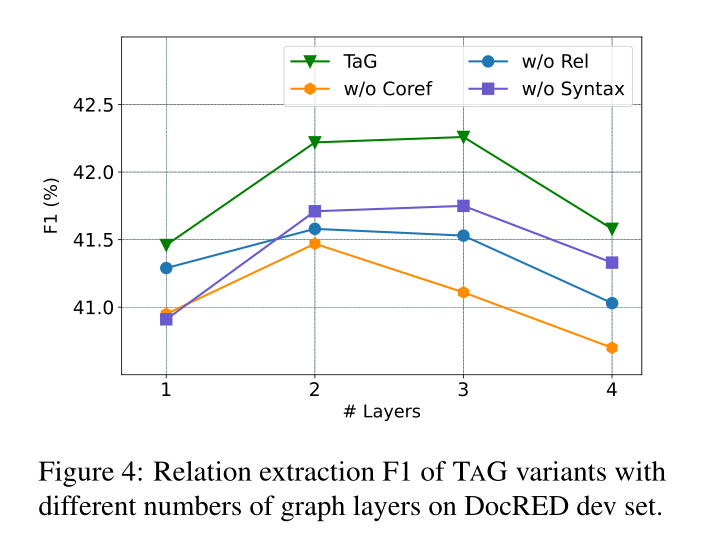
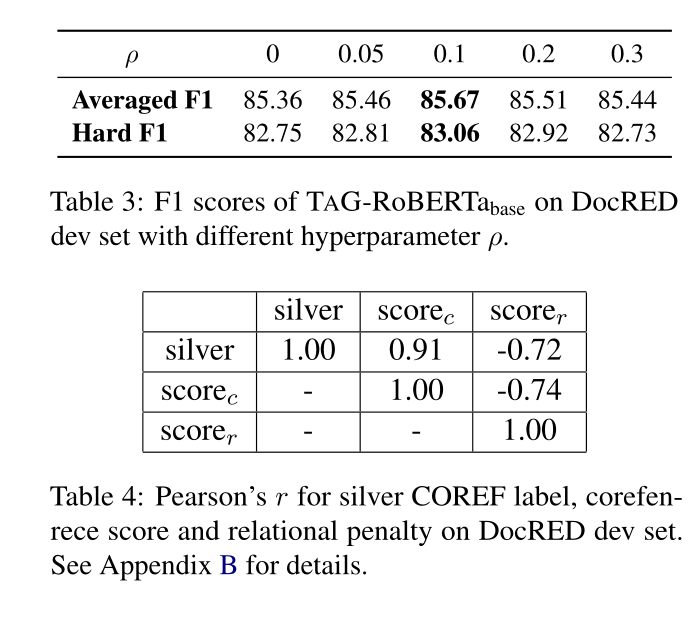
Experiments and Results

Conclusion

在本文中，我们提出了TAG，一种新的table-to-graph生成模型，用于联合提取文档中的实体和关系。与以前的方法不同，我们将共指解析和关系提取的任务与表填充框架统一起来，并利用从粗到细的策略来促进这些子任务之间的信息共享。为了避免误差传播问题，我们在解码阶段采用HAC算法来增强具有RE预测的COREF。在广泛采用的基准DocRED上的实验结果表明，TAG显著优于以前的方法。进一步的分析也证实了我们模型中模块的有效性。