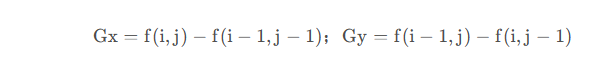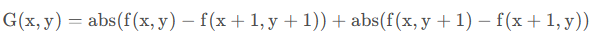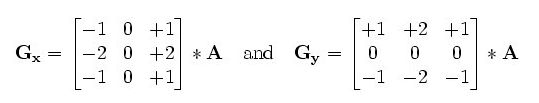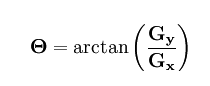图像处理之边缘检测(C++)
文章目录
前言
边缘检测是图像处理的基础,边缘检测主要是为了找到图像中亮度变化剧烈的像素点构成的集合,即图像的轮廓(边缘)。
传统边缘检测的主要有Roberts、Sobel、Prewitt、Laplacian、LOG、DOG等方法,本文介绍上述的边缘检测算子的实现。
原图:
一、Roberts算子
1.原理
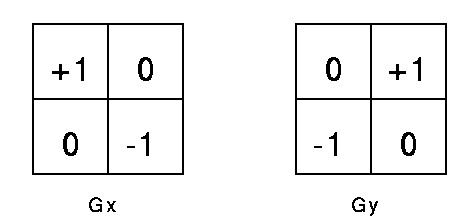
Roberts算子是一种斜向偏差分的梯度计算方法,采用对角方向相邻的两像素值之差,梯度的大小代表边缘的强度,梯度的方向与边缘的走向垂直。它是2X2算子模板。2个卷积核形成了Roberts算子。图像中的每一个点都用这2个核做卷积。
卷积核形式如下:
计算公式如下:
备注:采用绝对值相加减少计算量。
2.代码实现
#include <opencv.hpp>
#include <iostream>
/*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
*/
void roberts(const cv::Mat& src, cv::Mat& dst)
{
// 创建卷积核
cv::Mat kernel_x = (cv::Mat_<float>(2, 2) << 1, 0, 0, -1);
cv::Mat kernel_y = (cv::Mat_<float>(2, 2) << 0, 1, -1, 0);
// 卷积计算
// 卷积核翻转
cv::flip(kernel_x, kernel_x, -1);
cv::flip(kernel_y, kernel_y, -1);
// 相关性计算
cv::Mat dst_x, dst_y;
cv::filter2D(src, dst_x, kernel_x.depth(), kernel_x);
cv::filter2D(src, dst_y, kernel_y.depth(), kernel_y);
// 绝对值转换
cv::convertScaleAbs(dst_x, dst_x);
cv::convertScaleAbs(dst_y, dst_y);
// 计算梯度
dst = dst_x + dst_y;
cv::normalize(dst, dst, 0, 255, cv::NORM_MINMAX,CV_8UC1);
}
int main()
{
// 读取图片
std::string filepath = "F://work_study//algorithm_demo//regionGrow_test.jpg";
cv::Mat src = cv::imread(filepath, cv::IMREAD_GRAYSCALE);
if (src.empty())
{
return -1;
}
cv::Mat dst;
roberts(src, dst);
// 保存图片
cv::imwrite("dst.jpg", dst);
system("pause");
return 0;
}
二、Sobel算子
1.原理
Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。它结合高斯平滑和微分求导,用来计算图像灰度函数的近似梯度(读者可以尝试分离卷积核,即可看出卷积核是由一个求解水平梯度或者垂直梯度的卷积核和非归一化的高斯平滑相乘得到)。在图像的任何一点使用此算子,将会产生对应的梯度矢量或是其法矢量。它对噪声具有平滑作用,提供较为精确的边缘方向信息,边缘定位精度不够高。
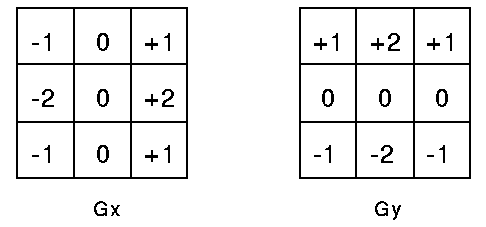
卷积核形式:
计算公式如下:
2.代码实现
/*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
* @brief sobel算子实现
*/
void sobel(const cv::Mat& src, cv::Mat& dst) {
// 创建卷积核
cv::Mat kernel_x = (cv::Mat_<float>(3,3) << -1, 0, 1, -2, 0, 2, -1, 0, 1);
cv::Mat kernel_y = (cv::Mat_<float>(3, 3) << 1, 2, 1, 0, 0, 0, -1, -2, -1);
// 卷积运算
// 翻转卷积核
cv::flip(kernel_x, kernel_x, -1);
cv::flip(kernel_y, kernel_y, -1);
// 相关性计算
cv::Mat dst_x, dst_y;
cv::filter2D(src, dst_x, kernel_x.depth(), kernel_x);
cv::filter2D(src, dst_y, kernel_y.depth(), kernel_y);
cv::convertScaleAbs(dst_x, dst_x);
cv::convertScaleAbs(dst_y, dst_y);
cv::normalize(dst_x + dst_y, dst, 0, 255, cv::NORM_MINMAX, CV_8U);
}
int main()
{
// 读取图片
std::string filepath = "F://work_study//algorithm_demo//regionGrow_test.jpg";
cv::Mat src = cv::imread(filepath, cv::IMREAD_GRAYSCALE);
if (src.empty())
{
return -1;
}
cv::Mat dst;
sobel(src, dst);
// 保存图片
cv::imwrite("dst.jpg", dst);
system("pause");
return 0;
}
三、Prewitt算子
1.原理
Prewitt算子的计算步骤如sobel算子,将方向的差分运算和局部平均相结合的方法(通过分离卷积核即可得出结论,不多赘述),也是取水平和垂直两个卷积核来分别对图像中各个像素点做卷积运算,所不同的是,Sobel 算子是先做加权平均然后再微分,Prewitt 算子是先平均后求微分。由于采用了局部灰度平均,容易检测出伪边缘,且边缘定位精度较低。
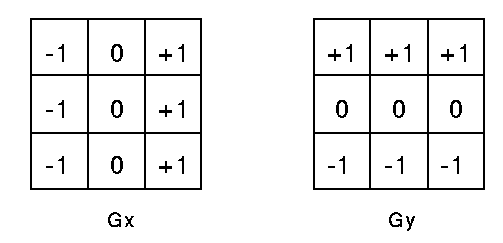
卷积核形式:
计算公式:
2.代码实现
/*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
* @brief prewitt算子实现
*/
void prewitt(const cv::Mat& src, cv::Mat& dst) {
// 创建卷积核
cv::Mat kernel_x = (cv::Mat_<float>(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1);
cv::Mat kernel_y = (cv::Mat_<float>(3, 3) << 1, 1, 1, 0, 0, 0, -1, -1, -1);
// 卷积运算
// 翻转卷积核
cv::flip(kernel_x, kernel_x, -1);
cv::flip(kernel_y, kernel_y, -1);
// 相关性计算
cv::Mat dst_x, dst_y;
cv::filter2D(src, dst_x, kernel_x.depth(), kernel_x);
cv::filter2D(src, dst_y, kernel_y.depth(), kernel_y);
cv::convertScaleAbs(dst_x, dst_x);
cv::convertScaleAbs(dst_y, dst_y);
cv::normalize(dst_x + dst_y, dst, 0, 255, cv::NORM_MINMAX, CV_8U);
}
int main()
{
// 读取图片
std::string filepath = "F://work_study//algorithm_demo//regionGrow_test.jpg";
cv::Mat src = cv::imread(filepath, cv::IMREAD_GRAYSCALE);
if (src.empty())
{
return -1;
}
cv::Mat dst;
prewitt(src, dst);
// 保存图片
cv::imwrite("prewitt_dst.jpg", dst);
system("pause");
return 0;
}
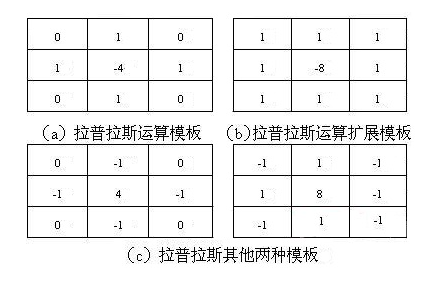
四、Laplacian算子
1.原理
它不依赖于边缘方向的二阶微分算子,对图像中的阶跃型边缘点定位准确,该算子对噪声非常敏感,它使噪声成分得到加强,这两个特性使得该算子容易丢失一部分边缘的方向信息,造成一些不连续的检测边缘,同时抗噪声能力比较差,由于其算法可能会出现双像素边界,常用来判断边缘像素位于图像的明区或暗区。
2.代码实现
/*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
* @brief prewitt算子实现
*/
void laplacian(const cv::Mat& src, cv::Mat& dst) {
// 创建卷积核
//cv::Mat kernel = (cv::Mat_<float>(3, 3) << 0, 1, 0, 1, -4, 1, 0, 1, 0);
cv::Mat kernel = (cv::Mat_<float>(3, 3) << 1, 1, 1, 1, -8, 1, 1, 1, 1);
// 卷积运算
// 翻转卷积核
cv::flip(kernel, kernel, -1);
// 相关性计算
cv::filter2D(src, dst, kernel.depth(), kernel);
cv::convertScaleAbs(dst, dst);
cv::normalize(dst, dst, 0, 255, cv::NORM_MINMAX, CV_8U);
}
int main()
{
// 读取图片
std::string filepath = "F://work_study//algorithm_demo//regionGrow_test.jpg";
cv::Mat src = cv::imread(filepath, cv::IMREAD_GRAYSCALE);
if (src.empty())
{
return -1;
}
cv::Mat dst;
laplacian(src, dst);
// 保存图片
cv::imwrite("laplacian.jpg", dst);
system("pause");
return 0;
}
五、LOG算子
1.原理
高斯拉普拉斯算子Lapacian of gaussian先对图像进行高斯平滑滤波处理,然后再与Laplacian算子进行卷积。其处理过程:灰度-高斯-拉普拉斯-负值为0。
2.代码实现
/*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
* @brief LOG算子实现
*/
void LOG(const cv::Mat& src, cv::Mat& dst) {
// 创建卷积核
cv::Mat kernel = (cv::Mat_<float>(5, 5) << 0, 0, -1, 0, 0,
0, -1, -2, -1, 0,
-1, -2, 16, -2, -1,
0, -1, -2, -1, 0,
0, 0, -1, 0, 0);
// 卷积运算(卷积核对称无需翻转)
cv::filter2D(src, dst, kernel.depth(), kernel);
cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
dst.convertTo(dst, CV_8U);
}
/*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
* @brief LOG算子实现
*/
void LOG1(const cv::Mat& src, cv::Mat& dst) {
// 高斯滤波
cv::GaussianBlur(src, dst, cv::Size(5, 5),0.5);
// laplacian
laplacian(dst, dst);
cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
dst.convertTo(dst, CV_8U);
}
int main()
{
// 读取图片
std::string filepath = "F://work_study//algorithm_demo//regionGrow_test.jpg";
cv::Mat src = cv::imread(filepath, cv::IMREAD_GRAYSCALE);
if (src.empty())
{
return -1;
}
cv::Mat dst;
LOG(src, dst);
// 保存图片
cv::imwrite("LOG.jpg", dst);
system("pause");
return 0;
}
六、DOG算子
1.原理
Difference of Gaussian(DOG)是高斯函数的差分。它是可以通过将图像与高斯函数进行卷积得到一幅图像的低通滤波结果,它对高斯拉普拉斯LoG的近似,在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减,得到DoG的响应值图像。
公式证明:
计算步骤:
使用两个不同标准差的高斯核平滑图像,然后结果相减,负值为0,获得边缘检测结果。
2.代码实现
*
* @param const cv::Mat& src 输入图像
* @param cv::Mat& dst 输出图像
* @brief DOG算子实现
*/
void DOG(const cv::Mat& src, cv::Mat& dst,double sigma,int k) {
cv::Mat dst_x, dst_y;
cv::GaussianBlur(src, dst_x, cv::Size(3, 3), sigma);
cv::GaussianBlur(src, dst_y, cv::Size(3, 3), k*sigma);
dst = dst_x - dst_y;
cv::threshold(dst, dst, 0, 255, cv::THRESH_BINARY);
dst.convertTo(dst, CV_8U);
}
int main()
{
// 读取图片
std::string filepath = "F://work_study//algorithm_demo//regionGrow_test.jpg";
cv::Mat src = cv::imread(filepath, cv::IMREAD_GRAYSCALE);
if (src.empty())
{
return -1;
}
cv::Mat dst;
DOG(src, dst,1,2);
// 保存图片
cv::imwrite("DOG.jpg", dst);
system("pause");
return 0;
}
总结
本文介绍了图像处理中的边缘检测算法,包括了Roberts、Sobel、Prewitt、laplacian、DOG、LOG等算子的C++实现和原理介绍,欢迎大家指出问题和交流讨论。
参考资料:
高斯滤波(Gauss filtering)
图像处理 | 最常用的边缘检测详解与代码(Robert, Sober, Prewitt, Canny, Kirsch, Laplacian, LOG, DOG算子)
LOG算子实现