提示：本文是基于吴恩达老师机器学习视频总结

一、反向传播

关于反向传播的详细解释请访问此文章
链接: 保姆级学会反向传播

二、梯度检测

在进行神经网络的具体实现的时候，很容易出bug，因此通常会使用梯度检测的方法来检验神经网络的实现是否正确。

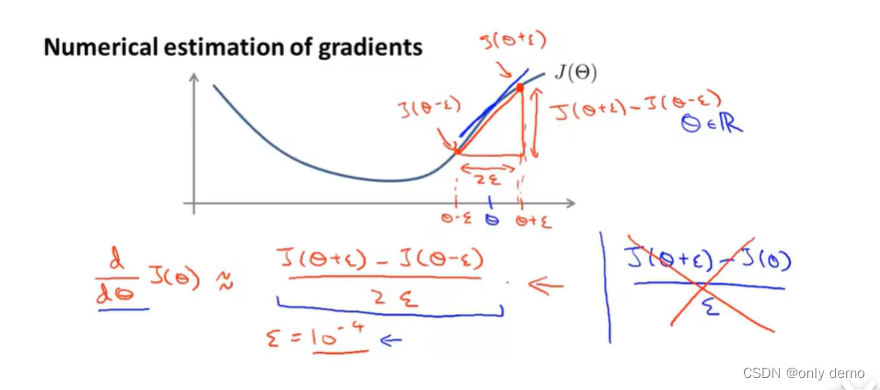
具体的思想就是我们通常会使用一个表达式来近似某一点的导数，如下图所示：

需要注意的点有以下几个：
1、ε通常是一个很小的数，当ε无限小，其实取极限就是导数。
2、上图中使用的双侧差分。但是有人会使用[J(θ+ε)-J(θ)]/ε，这种叫做单侧差分。但是单侧差分准确率一般没有双侧差分高，因此一般不使用。

上图是我们当θ为实数时，我们可以延伸到向量形式，如下图所示

具体实现的伪代码如下图所示：

需要注意的是：
使用了这个方法之后，我们就需要比较所有参数的偏导数的计算和我们在进行反向传播得到的梯度进行比较。验证这两个数是否近似相等，如果是的话说明反向传播的计算是正确的，否则计算是有问题的。
此外，我们需要记住，在进行实际的计算（计算得到最优theta）的过程中，我们必须要关掉梯度检测的代码，否则会运行的很慢。因为反向传播是效率很高的算法，而梯度检测则是很慢的，因此验证正确后就需要关掉。

三、随机初始化

在线性回归和逻辑回归中，我们都需要初始化θ数组，并且我们通常会用0来进行初始化来简化计算
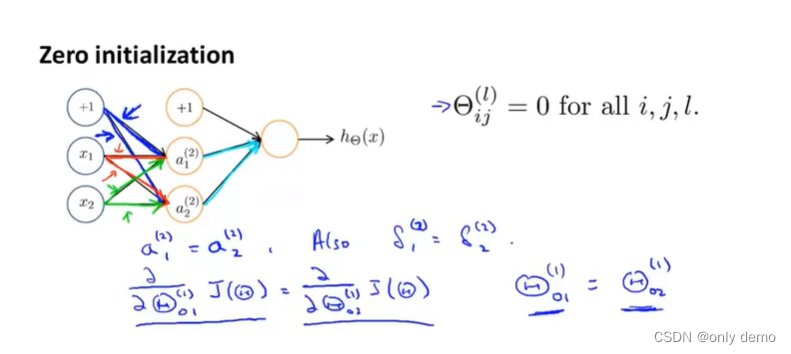
同样地，在神经网络中，我们也需要初始化θ数组，但是这时我们就不能使用0来进行初始化。具体问题如下图所示：

对于上图我们需要注意的有以下几点：
1、如果所有参数都初始化为0，那么将会导致所有权重都一样。也就是最开始a₁⁽²⁾=a₂⁽²⁾，紧接着所有参数都是一样的。
2、在进行梯度变化的过程中，虽然之后都会进行变化，但是权重会始终保持一样，即蓝色的权重等于蓝色的权重，红色的权重等于红色的权重，绿色的权重等于绿色的权重，这样就会一直使a₁⁽²⁾=a₂⁽²⁾，从而得不到很好的学习效果。

为了解决这个问题，就提出了随机初始化的思想，就是采用随机数来赋值权重，我们会对Θ在一个范围内进行随机赋值，如下图所示

这里的ε和梯度检验的ε没有任何关系。

四、组合

下面通过前面学到的知识来整合神经网络构建的步骤。
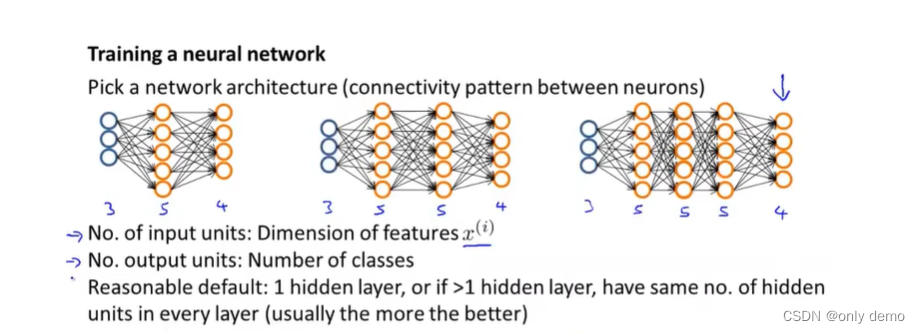
1、我们要构建神经网络的整体架构。

我们需要注意以下几个点：
1、首先要确定输入层和输出层的单元数
2、然后，较为合理的默认选择是只有一层隐藏层（如图一架构）。如果有多个隐藏层，那么每个隐藏层的单元数最好相同（虽然更多的单元数会得到更好的结果，但是也要考虑到计算量）
3、隐藏层的单元数还应该和输入层的单元数相匹配，可以是1倍、2倍、3倍4倍等。

2、随机初始化权重
通常我们会把权重初始化为很小的值，接近于0

3、执行前向传播算法
对于任意的x(i)都计算出对应的hθ(x(i))，也就是得到输出层的向量

4、代码实现计算代价函数J(θ)

5、执行反向传播算法
通过执行反向传播算法，计算

也就是进行如下过程：（第一次实现的时候建议用for循环，不要用向量化)

6、进行梯度检测
比较反向传播算法得到的导数值和估计的导数值是否近似相等。
检测完成后记得禁用梯度检测

7、进行梯度下降或使用高级优化算法
使用梯度下降或高级优化算法和反向传播算法相结合，从而去得到J(θ)的最小值和最优的权重θ。
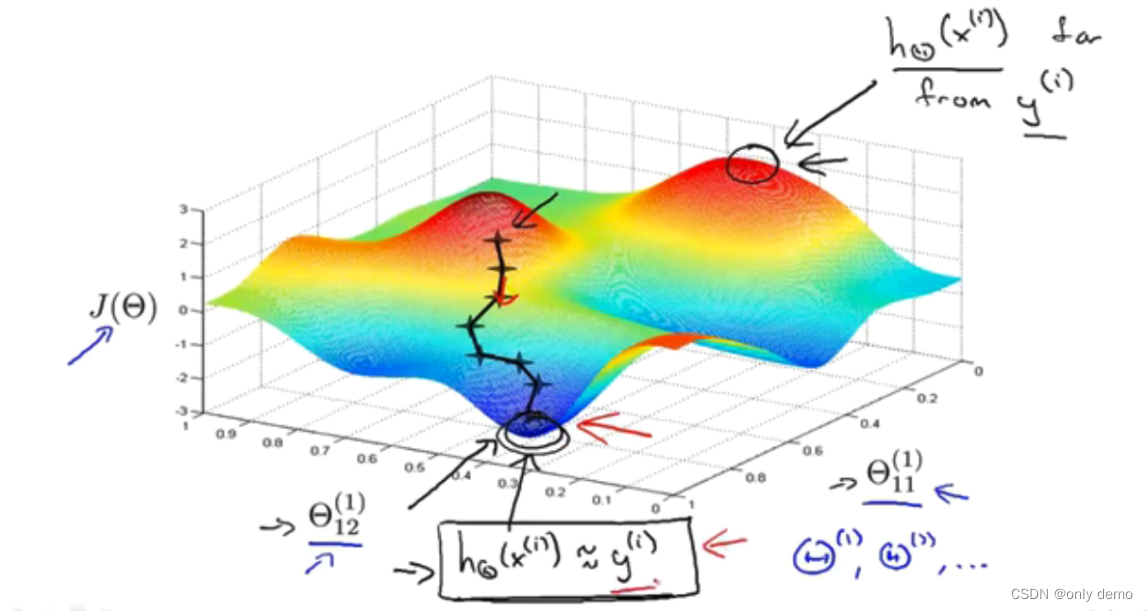
另外,因为神经网路的代价函数不是一个凸函数，因此可能寻找到的是局部最小值，但是对于大部分情况还是效果比较好的。

下面这个图就再一次展示了梯度下降的原理。其实反向传播算法计算的偏导数就是在计算梯度下降的方向。