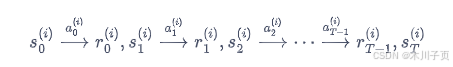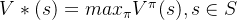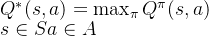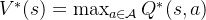本章接上文,所以标题直接从4.4开始。
4.4 马尔可夫决策过程(MDP)
4.2和4.3所讲的马尔可夫过程和马尔科夫奖励过程都是自发改变的随机过程,如果有一个来自外界的“刺激”来共同改变这个随机过程,就有了马尔可夫决策过程(Markov decision process,MDP).我们将这个来自外界的刺激称为智能体(agent)的动作,在马尔可夫奖励过程(MRP)的基础上加入动作,就得到了马尔可夫决策过程(MDP)。MDP由元组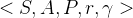
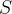
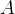
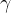
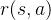


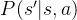



MDP跟MRP其实很相似,就差了一个主观因素"动作
这是一个循环的过程:智能体(Agent)根据当前的状态




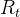
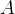
4.4.1 策略
智能体的策略通常用字母



那么在MDP也可以定义类似的价值函数,此时的价值函数跟策略是有关的。不同的策略在同一个状态下的价值很可能也是不一样的。这是因为不同策略采取不同的动作,之后会遇到不同的状态,获得不同的奖励,所以他们的累计奖励的期望时不同的,即状态价值不同。
4.4.2 状态价值函数
用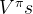



4.4.3 动作价值函数
与MRP不同,MDP多了一个“动作
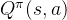



状态价值函数和动作价值函数之间是存在关系的,在使用策略


使用策略


4.4.4 贝尔曼期望方程
在贝尔曼方程中加上“期望”二字是为了与接下来的贝尔曼最优方程进行区分。我们通过简单推导就可以分别得到两个价值函数的贝尔曼期望方程:
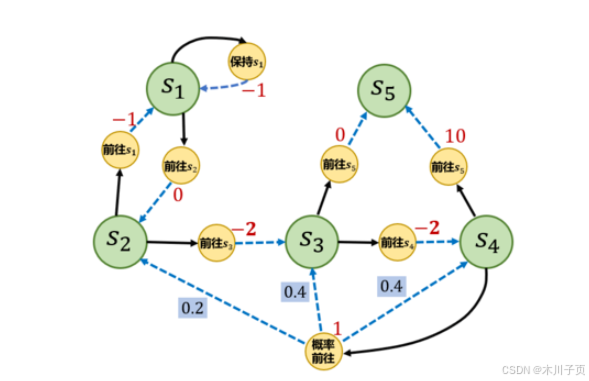
下图是一个马尔可夫决策过程的简单例子,其中每个深色圆圈代表一个状态,一共有从




每个浅色小圆圈旁的数字代表在某个状态下采取某个动作能获得的奖励。虚线箭头代表采取动作后可能转移到的状态,箭头边上的数字代表转移概率,如果没有数字则表示转移概率为 1。例如,在






接下来我们编写代码来表示上图 的马尔可夫决策过程,并定义两个策略。第一个策略是一个完全随机策略,即在每个状态下,智能体会以同样的概率选取它可能采取的动作。例如,在


S = ["s1", "s2", "s3", "s4", "s5"] # 状态集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"] # 动作集合
# 状态转移函数
P = {
"s1-保持s1-s1": 1.0,
"s1-前往s2-s2": 1.0,
"s2-前往s1-s1": 1.0,
"s2-前往s3-s3": 1.0,
"s3-前往s4-s4": 1.0,
"s3-前往s5-s5": 1.0,
"s4-前往s5-s5": 1.0,
"s4-概率前往-s2": 0.2,
"s4-概率前往-s3": 0.4,
"s4-概率前往-s4": 0.4,
}
# 奖励函数
R = {
"s1-保持s1": -1,
"s1-前往s2": 0,
"s2-前往s1": -1,
"s2-前往s3": -2,
"s3-前往s4": -2,
"s3-前往s5": 0,
"s4-前往s5": 10,
"s4-概率前往": 1,
}
gamma = 0.5 # 折扣因子
MDP = (S, A, P, R, gamma)
# 策略1,随机策略
Pi_1 = {
"s1-保持s1": 0.5,
"s1-前往s2": 0.5,
"s2-前往s1": 0.5,
"s2-前往s3": 0.5,
"s3-前往s4": 0.5,
"s3-前往s5": 0.5,
"s4-前往s5": 0.5,
"s4-概率前往": 0.5,
}
# 策略2
Pi_2 = {
"s1-保持s1": 0.6,
"s1-前往s2": 0.4,
"s2-前往s1": 0.3,
"s2-前往s3": 0.7,
"s3-前往s4": 0.5,
"s3-前往s5": 0.5,
"s4-前往s5": 0.1,
"s4-概率前往": 0.9,
}
# 把输入的两个字符串通过“-”连接,便于使用上述定义的P、R变量
def join(str1, str2):
return str1 + '-' + str2接下来我们准备计算该MDP下,一个策略

同理,我们计算采取动作的概率与使



于是,我们构建得到了一个MRP: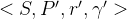
我们接下来就编写代码来实现该方法,计算用随机策略(也就是代码中的Pi_1)时的状态价值函数。为了简单起见,我们直接给出转化后的 MRP 的状态转移矩阵和奖励函数。
def compute(P, rewards, gamma, states_num):
''' 利用贝尔曼方程的矩阵形式计算解析解,states_num是MRP的状态数 '''
rewards = np.array(rewards).reshape((-1, 1)) # 将rewards写成列向量形式
value = np.dot(np.linalg.inv(np.eye(states_num, states_num) - gamma * P),
rewards)
return value
gamma = 0.5
# 转化后的MRP的状态转移矩阵
P_from_mdp_to_mrp = [
[0.5, 0.5, 0.0, 0.0, 0.0],
[0.5, 0.0, 0.5, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.5, 0.5],
[0.0, 0.1, 0.2, 0.2, 0.5],
[0.0, 0.0, 0.0, 0.0, 1.0],
]
P_from_mdp_to_mrp = np.array(P_from_mdp_to_mrp)
R_from_mdp_to_mrp = [-0.5, -1.5, -1.0, 5.5, 0]
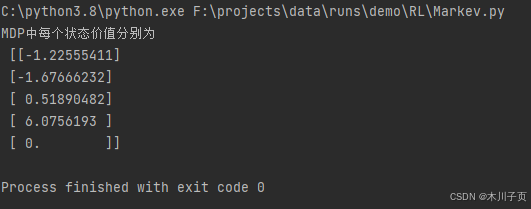
V = compute(P_from_mdp_to_mrp, R_from_mdp_to_mrp, gamma, 5)
print("MDP中每个状态价值分别为\n", V)结果:
这个 MRP 解析解的方法在状态动作集合比较大的时候不是很适用,那有没有其他的方法呢?下一章将介绍用动态规划算法来计算得到价值函数。4.5 节将介绍用蒙特卡洛方法来近似估计这个价值函数,用蒙特卡洛方法的好处在于我们不需要知道 MDP 的状态转移函数和奖励函数,它可以得到一个近似值,并且采样数越多越准确。
4.5 蒙特卡洛方法
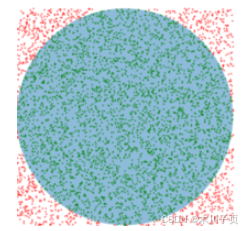
蒙特卡洛方法(Monte-Carlo methods)也被称为统计模拟方法,是一种基于概率统计的数值计算方法。运用蒙特卡洛方法时,我们通常使用重复随机抽样,然后运用概率统计方法来从抽样结果中归纳出我们想求的目标的数值估计。一个简单的例子是用蒙特卡洛方法来计算圆的面积。例如,如下图所示的正方形内部随机产生若干个点,细数落在圆中点的个数,圆的面积与正方形面积之比就等于圆中点的个数与正方形中点的个数之比。如果我们随机产生的点的个数越多,计算得到圆的面积就越接近于真实的圆的面积。
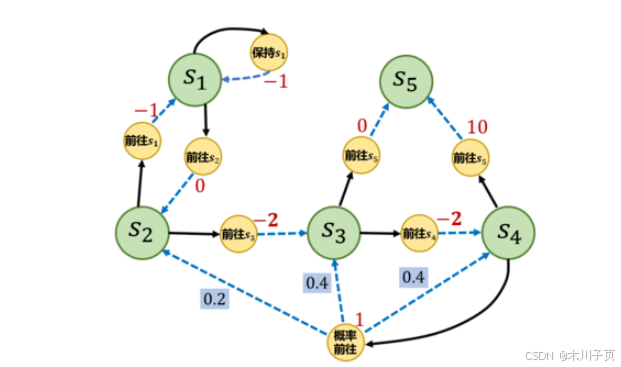
我们现在介绍如何用蒙特卡洛方法来估计一个策略在一个马尔可夫决策过程中的状态价值函数。原来的某个状态的价值是它的期望回报,那么一个很直观的想法就是用策略在MDP上采样很多条序列(这个序列就是从某状态开始一直到结束状态),计算从这个状态出发的回报再求其期望就可以了。公式如下:
在一条序列中,可能没有出现过这个状态,可能只出现过一次这个状态,也可能出现过很多次这个状态。我们介绍的蒙特卡洛价值估计方法会在该状态每一次出现时计算它的回报。还有一种选择是一条序列只计算一次回报,也就是这条序列第一次出现该状态时计算后面的累积奖励,而后面再次出现该状态时,该状态就被忽略了。假设我们现在用策略

(1)使用策略
(2) 对每一条序列中的每一时间步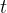

- 更新状态
的计数器
- 更新状态
的总回报
(3)每一个状态的价值被估计为回报的平均值.
根据大数定律,当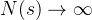
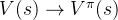

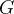
接下来我们用代码定义一个采样函数。采样函数需要遵守状态转移矩阵和相应的策略,每次将(s,a,r,s_next)元组放入序列中,直到到达终止序列。然后我们通过该函数,用随机策略在下面图的 MDP 中随机采样几条序列。
def sample(MDP, Pi, timestep_max, number):
''' 采样函数,策略Pi,限制最长时间步timestep_max,总共采样序列数number '''
S, A, P, R, gamma = MDP
episodes = []
for _ in range(number):
episode = []
timestep = 0
s = S[np.random.randint(4)] # 随机选择一个除s5以外的状态s作为起点
# 当前状态为终止状态或者时间步太长时,一次采样结束
while s != "s5" and timestep <= timestep_max:
timestep += 1
rand, temp = np.random.rand(), 0
# 在状态s下根据策略选择动作
for a_opt in A:
temp += Pi.get(join(s, a_opt), 0)
if temp > rand:
a = a_opt
r = R.get(join(s, a), 0)
break
rand, temp = np.random.rand(), 0
# 根据状态转移概率得到下一个状态s_next
for s_opt in S:
temp += P.get(join(join(s, a), s_opt), 0)
if temp > rand:
s_next = s_opt
break
episode.append((s, a, r, s_next)) # 把(s,a,r,s_next)元组放入序列中
s = s_next # s_next变成当前状态,开始接下来的循环
episodes.append(episode)
return episodes
# 采样5次,每个序列最长不超过20步
episodes = sample(MDP, Pi_1, 20, 5)
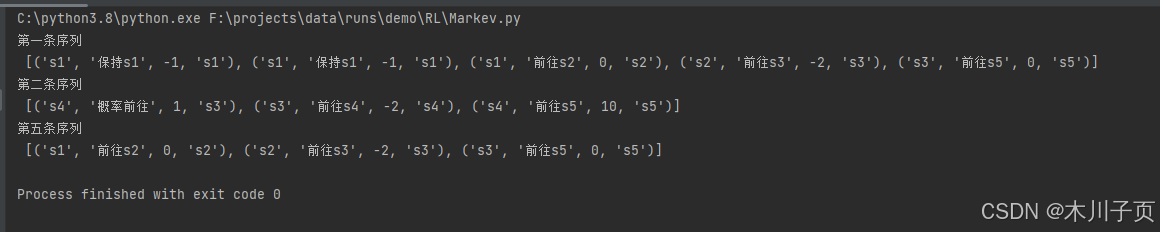
print('第一条序列\n', episodes[0])
print('第二条序列\n', episodes[1])
print('第五条序列\n', episodes[4])结果:
# 对所有采样序列计算所有状态的价值
def MC(episodes, V, N, gamma):
for episode in episodes:
G = 0
for i in range(len(episode) - 1, -1, -1): #一个序列从后往前计算
(s, a, r, s_next) = episode[i]
G = r + gamma * G
N[s] = N[s] + 1
V[s] = V[s] + (G - V[s]) / N[s]
timestep_max = 20
# 采样1000次,可以自行修改
episodes = sample(MDP, Pi_1, timestep_max, 1000)
gamma = 0.5
V = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
N = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
MC(episodes, V, N, gamma)
print("使用蒙特卡洛方法计算MDP的状态价值为\n", V)结果:
可以看到用蒙特卡洛方法估计得到的状态价值和我们用 MRP 解析解得到的状态价值是很接近的。这得益于我们采样了比较多的序列,感兴趣的读者可以尝试修改采样次数,然后观察蒙特卡洛方法的结果。
4.6最优策略
强化学习的目标通常是找到一个策略,使得智能体从初始状态出发能获得最多的期望回报。我们首先定义策略之间的偏序关系:当且仅当对于任意的状态
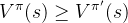


最优策略都有相同的状态价值函数,我们称之为最优状态价值函数,表示为:
同理,我们定义最优动作价值函数:
为了使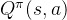
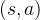
这与在普通策略下的状态价值函数和动作价值函数之间的关系是一样的。另一方面,最优状态价值是选择此时使最优动作价值最大的那一个动作时的状态价值:
4.7.1 贝尔曼最优方程
根据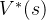
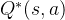
4.8 总结
这两节(1章)从零开始介绍了马尔可夫决策过程的基础概念知识,并讲解了如何通过求解贝尔曼方程得到状态价值的解析解以及如何用蒙特卡洛方法估计各个状态的价值。马尔可夫决策过程是强化学习中的基础概念,强化学习中的环境就是一个马尔可夫决策过程。我们接下来将要介绍的强化学习算法通常都是在求解马尔可夫决策过程中的最优策略。

![V^\pi(s) =E_\pi[G_t|S_t = s]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9WJTVFJTVDcGklMjhzJTI5JTIwJTNERV8lNUNwaSU1QkdfdCU3Q1NfdCUyMCUzRCUyMHMlNUQ%3D)
![Q^\pi(s,a) = E[G_t|S_t=s, A_t = a]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9RJTVFJTVDcGklMjhzJTJDYSUyOQ%3D%3D%20%3D%20E%5BG_t%7CS_t%3Ds%2C%20A_t%20%3D%20a%5D)
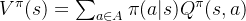

![Q^\pi(s,a) = E_\pi [R_t + \gamma Q^\pi(S_{t+1}, A_{t+1} | S_t = s, A_t = a)]\\](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9RJTVFJTVDcGklMjhzJTJDYSUyOQ%3D%3D%20%3D%20E_%5Cpi%20%5BR_t%20+%20%5Cgamma%20Q%5E%5Cpi%28S_%7Bt+1%7D%2C%20A_%7Bt+1%7D%20%7C%20S_t%20%3D%20s%2C%20A_t%20%3D%20a%29%5D%5C%5C)
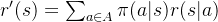
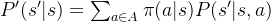
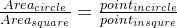
![V^\pi(s) = E_{\pi}[G_t|S_t = s] \approx \frac{1}{N} \sum^N_{i=1}G^{(i)}_t](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9WJTVFJTVDcGklMjhzJTI5JTIwJTNEJTIwRV8lN0IlNUNwaSU3RCU1QkdfdCU3Q1NfdCUyMCUzRCUyMHMlNUQlMjAlNUNhcHByb3glMjAlNUNmcmFjJTdCMSU3RCU3Qk4lN0QlMjAlNUNzdW0lNUVOXyU3QmklM0QxJTdERyU1RSU3QiUyOGklMjklN0RfdA%3D%3D)