5.1简介
动态规划(Dynamic Programming DP)是一类优化方法,在给定一个用马尔可夫决策过程描述的完备环境模型的情况下,其可以计算最优的策略。对于强化学习问题,传统的DP算法的作用有限。但其提供了一个必要的基础,为其他方法提供了一种近似。
基于动态规划的强化学习算法主要有两种:一是策略迭代(policy iteration),二是价值迭代(value iteration)。其中,策略迭代由两部分组成:策略评估(policy evaluation)和策略提升(policy improvement)。具体来说,策略迭代中的策略评估使用贝尔曼期望方程来得到一个策略的状态价值函数,这是一个动态规划的过程;而价值迭代直接使用贝尔曼最优方程来进行动态规划,得到最终的最优状态价值。
在本节里面,我们假设环境是一个有限的MDP,也就是说,假设动作集合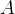
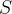
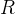
5.2 悬崖漫步环境
本节使用策略迭代和价值迭代来求解悬崖漫步(Cliff Walking)这个环境中的最优策略。接下来先简单介绍一下该环境。
悬崖漫步是一个非常经典的强化学习环境,它要求一个智能体从起点出发,避开悬崖行走,最终到达目标位置。如上图 所示,有一个 4×12 的网格世界,每一个网格表示一个状态。智能体的起点是左下角的状态,目标是右下角的状态,智能体在每一个状态都可以采取 4 种动作:上、下、左、右。如果智能体采取动作后触碰到边界墙壁则状态不发生改变,否则就会相应到达下一个状态。环境中有一段悬崖,智能体掉入悬崖或到达目标状态都会结束动作并回到起点,也就是说掉入悬崖或者达到目标状态是终止状态。智能体每走一步的奖励是 −1,掉入悬崖的奖励是 −100。
其实是有这个现成的悬崖漫步的环境的,别人做的也很好,但是呢,为了让大家更加清楚的理解,所以我们自己写一遍。
# -*- coding: utf-8 -*-
"""
@File : CliffWalkingEnv.py
@Author : Administrator
@Time : 2024-07-12 13:56
@IDE : PyCharm
@Version :
@comment : ···
"""
class CliffWalkingEnv:
"""悬崖漫步环境"""
def __init__(self, ncol=12, nrow=4):
self.ncol = ncol #定义网格世界的列
self.nrow = nrow #定义网格世界的行
#转移矩阵P[state][action] = [(P, next_state, reward, done)]
self.P = self.createP()
def createP(self):
#初始化
P = [[[] for j in range(4)] for i in range(self.nrow * self.ncol)]
#4种动作,change[0]:上;change[1]:下;change[2]:左;change[3]:右;
#初始位置定义在左上角
change = [[0, -1],[0, 1],[-1, 0],[1, 0]]
for i in range(self.nrow):
for j in range(self.ncol):
for a in range(4):
# 位置在悬崖或者目标状态,因为无法进行继续交互,所以任何动作奖励都为0
if i == self.nrow - 1 and j > 0:
P[i * self.ncol + j][a] = [1, i * self.ncol + j, 0, True]
continue
# 其他位置
next_x = min(self.ncol - 1, max(0, j + change[a][0]))
next_y = min(self.nrow - 1, max(0, i + change[a][1]))
next_state = next_y * self.ncol + next_x
reward = -1
done = False
# 下一个位置在悬崖或者终点
if next_y == self.nrow - 1 and next_x > 0:
done = True
if next_x != self.ncol - 1:
reward = -100
P[i * self.ncol + j][a] = [(1, next_state, reward, done)]
return P
if __name__ == '__main__':
cliffWalkingEnv = CliffWalkingEnv()
4.3 策略迭代算法
策略迭代算法指的是策略评估和策略提升不断循环交替,直至到最后得到最优策略的过程,这里将会对这两个过程进行详细讲解。
4.3.1 策略评估
策略评估这一过程用来计算一个策略的状态价值函数,首先我们来回顾一下之前学习的贝尔曼期望方程:
其中,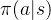



我们可以选定任意初始值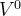
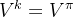
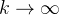
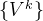
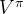
的值非常小,可以提前结束策略评估。这样做可以提升效率,并且得到的价值也非常接近真实的价值。
4.3.2 策略提升
使用策略评估计算得到当前策略的状态价值函数之后,我们可以据此来改进策略。假设此时对于策略
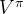






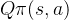





于是在任意状态
这就是策略提升定理。于是可以直接贪心的在每一个状态选择动作价值最大的动作,也就是
我们发现构造的贪心策略






策略提升定理的证明通过以下推导过程证明,使用上述提升公式得到的策略

可以看到,推导过程中的每一个时间步都用到局部动作价值优
"""
@File : PolicyIteration.py
@Author : Administrator
@Time : 2024-07-15 10:26
@IDE : PyCharm
@Version :
@comment : ···
"""
import copy
from CliffWalkingEnv import CliffWalkingEnv
class PolicyIteration:
""" 策略迭代算法 """
def __init__(self, env, theta, gamma):
self.env = env
self.v = [0] * self.env.ncol * self.env.nrow # 初始化价值为0
self.pi = [[0.25, 0.25, 0.25, 0.25]
for i in range(self.env.ncol * self.env.nrow)] # 初始化为均匀随机策略
self.theta = theta # 策略评估收敛阈值
self.gamma = gamma # 折扣因子
def policy_evaluation(self): # 策略评估
cnt = 1 # 计数器
while 1:
max_diff = 0
new_v = [0] * self.env.ncol * self.env.nrow
for s in range(self.env.ncol * self.env.nrow):
qsa_list = [] # 开始计算状态s下的所有Q(s,a)价值
for a in range(4):
qsa = 0
for res in self.env.P[s][a]:
p, next_state, r, done = res
qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
# 本章环境比较特殊,奖励和下一个状态有关,所以需要和状态转移概率相乘
qsa_list.append(self.pi[s][a] * qsa)
new_v[s] = sum(qsa_list) # 状态价值函数和动作价值函数之间的关系
max_diff = max(max_diff, abs(new_v[s] - self.v[s]))
self.v = new_v
if max_diff < self.theta: break # 满足收敛条件,退出评估迭代
cnt += 1
print("策略评估进行%d轮后完成" % cnt)
def policy_improvement(self): # 策略提升
for s in range(self.env.nrow * self.env.ncol):
qsa_list = []
for a in range(4):
qsa = 0
for res in self.env.P[s][a]:
p, next_state, r, done = res
qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
qsa_list.append(qsa)
maxq = max(qsa_list)
cntq = qsa_list.count(maxq) # 计算有几个动作得到了最大的Q值
# 让这些动作均分概率
self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]
print("策略提升完成")
return self.pi
def policy_iteration(self): # 策略迭代
while 1:
self.policy_evaluation()
old_pi = copy.deepcopy(self.pi) # 将列表进行深拷贝,方便接下来进行比较
new_pi = self.policy_improvement()
if old_pi == new_pi: break
现在我们已经写熬了环境代码和策略迭代代码。为了更好地展现最终的策略,接下来增加一个打印策略的函数,用于打印当前策略在每个状态下的价值以及智能体会采取的动作。对于打印出来的动作,我们用^o<o表示等概率采取向左和向上两种动作,ooo>表示在当前状态之采取向右动作。
def print_agent(agent, action_meaning, disaster=[], end=[]):
print("状态价值:")
for i in range(agent.env.nrow):
for j in range(agent.env.ncol):
# 为了输出美观,保持输出6个字符
print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')
print()
print("策略:")
for i in range(agent.env.nrow):
for j in range(agent.env.ncol):
# 一些特殊的状态,例如悬崖漫步中的悬崖
if (i * agent.env.ncol + j) in disaster:
print('****', end=' ')
elif (i * agent.env.ncol + j) in end: # 目标状态
print('EEEE', end=' ')
else:
a = agent.pi[i * agent.env.ncol + j]
pi_str = ''
for k in range(len(action_meaning)):
pi_str += action_meaning[k] if a[k] > 0 else 'o'
print(pi_str, end=' ')
print()
if __name__ == '__main__':
env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001
gamma = 0.9
agent = PolicyIteration(env, theta, gamma)
agent.policy_iteration()
print_agent(agent, action_meaning, list(range(37, 47)), [47])
输出如下:
策略评估进行60轮后完成
策略提升完成
策略评估进行72轮后完成
策略提升完成
策略评估进行44轮后完成
策略提升完成
策略评估进行12轮后完成
策略提升完成
策略评估进行1轮后完成
策略提升完成
状态价值:
-7.712 -7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
Process finished with exit code 0经过 5 次策略评估和策略提升的循环迭代,策略收敛了,此时将获得的策略打印出来。用贝尔曼最优方程去检验其中每一个状态的价值,可以发现最终输出的策略的确是最优策略。
4.4 价值迭代算法
从上面的代码运行结果可以发现,策略迭代中的策略评估需要进行很多轮才能收敛得到某一策略的状态函数,这需要很大的计算量,尤其是在状态和动作空间比较大的情况下。我们是否必须要等到策略评估完成后在进行策略提升呢?试想一下,可能出现这样的情况:虽然状态价值函数还没有收敛,但是不论接下来怎么更新状态价值,策略提升得到的都是同一个策略。如果只在策略评估中进行一轮价值更新,然后直接根据更新后的价值进行策略提升,这样的话就将其替换成了价值迭代算法,它可以被认为是一种策略评估只进行了一轮更新的策略迭代算法。但需要注意的是,价值迭代中不存在显式的策略,我们只维护一个状态价值函数。确切的说,价值迭代可以看成一种动态规划过程,他利用的是贝尔曼最优方程:
将其写成迭代更新的方式为:
价值迭代变是按照以上更新方式进行的。等到和
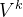
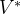

价值迭代算法流程如下:
我们现在来编写价值迭代的代码。
# -*- coding: utf-8 -*-
"""
@File : ValueIteration.py
@Author : Administrator
@Time : 2024-07-16 15:51
@IDE : PyCharm
@Version :
@comment : ···
"""
from CliffWalkingEnv import CliffWalkingEnv
class ValueIteration:
""" 价值迭代算法 """
def __init__(self, env, theta, gamma):
self.env = env
self.v = [0] * self.env.ncol * self.env.nrow # 初始化价值为0
self.theta = theta # 价值收敛阈值
self.gamma = gamma
# 价值迭代结束后得到的策略
self.pi = [None for i in range(self.env.ncol * self.env.nrow)]
def value_iteration(self):
cnt = 0
while 1:
max_diff = 0
new_v = [0] * self.env.ncol * self.env.nrow
for s in range(self.env.ncol * self.env.nrow):
qsa_list = [] # 开始计算状态s下的所有Q(s,a)价值
for a in range(4):
qsa = 0
for res in self.env.P[s][a]:
p, next_state, r, done = res
qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
qsa_list.append(qsa) # 这一行和下一行代码是价值迭代和策略迭代的主要区别
new_v[s] = max(qsa_list)
max_diff = max(max_diff, abs(new_v[s] - self.v[s]))
self.v = new_v
if max_diff < self.theta: break # 满足收敛条件,退出评估迭代
cnt += 1
print("价值迭代一共进行%d轮" % cnt)
self.get_policy()
def get_policy(self): # 根据价值函数导出一个贪婪策略
for s in range(self.env.nrow * self.env.ncol):
qsa_list = []
for a in range(4):
qsa = 0
for res in self.env.P[s][a]:
p, next_state, r, done = res
qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
qsa_list.append(qsa)
maxq = max(qsa_list)
cntq = qsa_list.count(maxq) # 计算有几个动作得到了最大的Q值
# 让这些动作均分概率
self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]
def print_agent(agent, action_meaning, disaster=[], end=[]):
print("状态价值:")
for i in range(agent.env.nrow):
for j in range(agent.env.ncol):
# 为了输出美观,保持输出6个字符
print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')
print()
print("策略:")
for i in range(agent.env.nrow):
for j in range(agent.env.ncol):
# 一些特殊的状态,例如悬崖漫步中的悬崖
if (i * agent.env.ncol + j) in disaster:
print('****', end=' ')
elif (i * agent.env.ncol + j) in end: # 目标状态
print('EEEE', end=' ')
else:
a = agent.pi[i * agent.env.ncol + j]
pi_str = ''
for k in range(len(action_meaning)):
pi_str += action_meaning[k] if a[k] > 0 else 'o'
print(pi_str, end=' ')
print()
if __name__ == '__main__':
env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001
gamma = 0.9
agent = ValueIteration(env, theta, gamma)
agent.value_iteration()
print_agent(agent, action_meaning, list(range(37, 47)), [47])
C:\python3.8\python.exe F:\projects\data\runs\demo\RL\ValueIteration.py
价值迭代一共进行14轮
状态价值:
-7.712 -7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710
-7.458 -7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900
-7.176 -6.862 -6.513 -6.126 -5.695 -5.217 -4.686 -4.095 -3.439 -2.710 -1.900 -1.000
-7.458 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
策略:
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
Process finished with exit code 0可以看到,解决同样的训练任务,价值迭代总共进行了数十轮,而策略迭代中的策略评估总共进行了数百轮,价值迭代中的循环次数远少于策略迭代。
4.5小结
本章讲解了强化学习中两个经典的动态规划算法:策略迭代算法和价值迭代算法,它们都能用于求解最优价值和最优策略。动态规划的主要思想是利用贝尔曼方程对所有状态进行更新。需要注意的是,在利用贝尔曼方程进行状态更新时,我们会用到马尔可夫决策过程中的奖励函数和状态转移函数。如果智能体无法事先得知奖励函数和状态转移函数,就只能通过和环境进行交互来采样(状态-动作-奖励-下一状态)这样的数据,我们将在之后的章节中讲解如何求解这种情况下的最优策略。
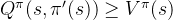
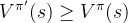

![V^\pi(s) \leq Q^\pi(s, \pi'(s)) \\ = \mathbb{E}^\pi \left[ R_t + \gamma V^\pi(S_{t+1}) \ \middle| \ S_t = s \right] \\ \leq \mathbb{E}^\pi \left[ R_t + \gamma Q^\pi(S_{t+1}, \pi'(S_{t+1})) \ \middle| \ S_t = s \right] \\ = \mathbb{E}^\pi \left[ R_t + \gamma R_{t+1} + \gamma^2 V^\pi(S_{t+2}) \ \middle| \ S_t = s \right] \\ \leq \mathbb{E}^\pi \left[ R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 V^\pi(S_{t+3}) \ \middle| \ S_t = s \right] \\ \vdots \\ \leq \mathbb{E}^\pi \left[ R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots \ \middle| \ S_t = s \right] \\ = V^{\pi'}(s)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9WJTVFJTVDcGk%3D%28s%29%20%5Cleq%20Q%5E%5Cpi%28s%2C%20%5Cpi%27%28s%29%29%20%5C%5C%20%3D%20%5Cmathbb%7BE%7D%5E%5Cpi%20%5Cleft%5B%20R_t%20+%20%5Cgamma%20V%5E%5Cpi%28S_%7Bt+1%7D%29%20%5C%20%5Cmiddle%7C%20%5C%20S_t%20%3D%20s%20%5Cright%5D%20%5C%5C%20%5Cleq%20%5Cmathbb%7BE%7D%5E%5Cpi%20%5Cleft%5B%20R_t%20+%20%5Cgamma%20Q%5E%5Cpi%28S_%7Bt+1%7D%2C%20%5Cpi%27%28S_%7Bt+1%7D%29%29%20%5C%20%5Cmiddle%7C%20%5C%20S_t%20%3D%20s%20%5Cright%5D%20%5C%5C%20%3D%20%5Cmathbb%7BE%7D%5E%5Cpi%20%5Cleft%5B%20R_t%20+%20%5Cgamma%20R_%7Bt+1%7D%20+%20%5Cgamma%5E2%20V%5E%5Cpi%28S_%7Bt+2%7D%29%20%5C%20%5Cmiddle%7C%20%5C%20S_t%20%3D%20s%20%5Cright%5D%20%5C%5C%20%5Cleq%20%5Cmathbb%7BE%7D%5E%5Cpi%20%5Cleft%5B%20R_t%20+%20%5Cgamma%20R_%7Bt+1%7D%20+%20%5Cgamma%5E2%20R_%7Bt+2%7D%20+%20%5Cgamma%5E3%20V%5E%5Cpi%28S_%7Bt+3%7D%29%20%5C%20%5Cmiddle%7C%20%5C%20S_t%20%3D%20s%20%5Cright%5D%20%5C%5C%20%5Cvdots%20%5C%5C%20%5Cleq%20%5Cmathbb%7BE%7D%5E%5Cpi%20%5Cleft%5B%20R_t%20+%20%5Cgamma%20R_%7Bt+1%7D%20+%20%5Cgamma%5E2%20R_%7Bt+2%7D%20+%20%5Cgamma%5E3%20R_%7Bt+3%7D%20+%20%5Ccdots%20%5C%20%5Cmiddle%7C%20%5C%20S_t%20%3D%20s%20%5Cright%5D%20%5C%5C%20%3D%20V%5E%7B%5Cpi%27%7D%28s%29)
