PAT 乙级讲题记录

1003 我要通过！ (20分)

题目描述

答案正确”是自动判题系统给出的最令人欢喜的回复。本题属于 PAT 的“答案正确”大派送 —— 只要读入的字符串满足下列条件，系统就输出“答案正确”，否则输出“答案错误”。

得到“答案正确”的条件是：

1.字符串中必须仅有 P、 A、 T这三种字符，不可以包含其它字符；
2.任意形如 xPATx 的字符串都可以获得“答案正确”，其中 x 或者是空字符串，或者是仅由字母 A 组成的字符串；
3.如果 aPbTc 是正确的，那么 aPbATca 也是正确的，其中 a、 b、 c 均或者是空字符串，或者是仅由字母 A 组成的字符串。

现在就请你为 PAT 写一个自动裁判程序，判定哪些字符串是可以获得“答案正确”的。

输入格式：

每个测试输入包含 1 个测试用例。第 1 行给出一个正整数 n ( $<$ 10)，是需要检测的字符串个数。接下来每个字符串占一行，字符串长度不超过 100，且不包含空格。

输出格式：

每个字符串的检测结果占一行，如果该字符串可以获得“答案正确”，则输出 YES，否则输出 NO。

样例
输入样例：

8
PAT																
PAAT														
AAPATAA													
AAPAATAAAA												
xPATx															
PT															
Whatever														
APAAATAA

输出样例:

YES
YES
YES
YES
NO
NO
NO
NO

Solution

条件1：仅包含P、A、T
条件2：P和T仅有一个，A $\ge$ 1
条件3：若 aPbTc 合法，那么 aPbATca 也合法我们可以得到，如果P和T中间的A的数量增加了1个，那么T之后的A的数量增加了a个。
令P前的A数量为x，P和T之间的A数量为y，T之后的A数量为z，可得：

x * y = z

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 100 + 5;
char s[SZ];

int main()
{
	int T;
	scanf("%d",&T);
	while(T --)
	{
		scanf("%s",s);
		int posp = 0,post = 0,nump = 0,numa = 0,numt = 0; // P的位置、T的位置、p的数量、a的数量、t的数量。 
		int prea = 0,ina = 0,posta = 0;// x 、 y 、 z 
		for(int i = 0;i < strlen(s);i ++)
		{
			if(s[i] == 'A') numa ++;
			if(s[i] == 'P')
			{
				posp = i;
				nump ++;
			}
			if(s[i] == 'T')
			{
				post = i;
				numt ++;
			}
		}
		if(nump == 1 && numt == 1 && numa >= 1 && nump + numa + numt == strlen(s)) //条件1、2 
		{
			prea = posp;
			ina = post - posp - 1;
			posta = numa - prea - ina;
			if(prea * ina == posta) printf("YES\n"); // 条件3 
			else printf("NO\n");
		} 
		else printf("NO\n");
	}
	return 0;
}

1013 数素数 (20分)

1013 数素数

题目描述

令 $P_i$ 表示第 i 个素数。现任给两个正整数 M $\le$ N $\le$ $10^4$ ，请输出 $P_M$ 到 $P_N$ 的所有素数。

输入格式：

输入在一行中给出 M 和 N，其间以空格分隔。

输出格式：

输出从 $P_M$ 到 $P_N$ 的所有素数，每 10 个数字占 1 行，其间以空格分隔，但行末不得有多余空格。

输入样例：

5 27

输出样例：

11 13 17 19 23 29 31 37 41 43
47 53 59 61 67 71 73 79 83 89
97 101 103

Solution

两种素数筛

埃氏筛
O( $n\log_2{\log_2n}$ )

在这里插入图片描述

for(int i = 2;i <= n;i ++)
{
	if(prime[i] == 0)
	{
		p[ ++ tot] = i;
		for(int j = 2;j * i <= n;j ++ )
			prime[j * i] = 1;	
	}
}

欧拉筛
O( $n$ )

埃氏筛的缺陷：同一个合数有可能被多个素数筛。
欧拉筛克服了这一缺陷，每个合数只被最小质因子来筛，复杂度也就是线性的。

int p[SZ],prime[SZ];

inline void e_prime(int N);
{ 
	int tot = 0;
	for(int i = 2;i <= N;i ++ )
	{
		if(prime[i] == 0) p[ ++ tot] = i;
		for(int j = 1;j <= tot && i * p[j] <= N;j ++)
		{
			prime[i * p[j]] = 1;
			if(i % p[j] == 0) break;
		}
	}
}

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 110000;
map<int,int>prime;
vector<int> p; 

/*inline void sieve() //埃氏筛
{
	for(int i = 2;i <= SZ;i ++)
	{
		if(prime[i] == 0)
		{
			p.push_back(i);
			for(int j = 2;j * i <= SZ;j ++) prime[j * i] = 1;
		}
	}
}*/

inline void e_prime() //欧拉筛
{	
	for(int i = 2;i <= SZ;i ++)
	{
		if(prime[i] == 0) p.push_back(i);
		for(int j = 0;j < p.size() && i * p[j] < SZ;j ++)
		{
			prime[i * p[j]] = 1;
			if(i % p[j] == 0) break;
		}
	}
}

int main()
{
	//sieve();
	e_prime();
	int n,m;
	scanf("%d%d",&n,&m);
	int cnt = 0;
	for(int i = n - 1;i <= m - 1;i ++)
	{
		cnt ++;
		if(i == m - 1) printf("%d",p[i]);
		else printf("%d%c",p[i],(cnt % 10 == 0) ? '\n' : ' ');
	}
	return 0;
}

1027 打印沙漏 (20分)

1027 打印沙漏

题目描述

本题要求你写个程序把给定的符号打印成沙漏的形状。例如给定17个“*”，要求按下列格式打印：

*****
 ***
  *
 ***
*****

所谓“沙漏形状”，是指每行输出奇数个符号；各行符号中心对齐；相邻两行符号数差2；符号数先从大到小顺序递减到1，再从小到大顺序递增；首尾符号数相等。

给定任意N个符号，不一定能正好组成一个沙漏。要求打印出的沙漏能用掉尽可能多的符号。

输入格式:

输入在一行给出1个正整数N（ $\le$ 1000）和一个符号，中间以空格分隔。

输出格式:

首先打印出由给定符号组成的最大的沙漏形状，最后在一行中输出剩下没用掉的符号数。

输入样例:

19 *

输出样例:

*****
 ***
  *
 ***
*****
2

Solution

首先，计算出除了最中间的一行，还要向上向下延伸的行数。
$a_n = 2 * n + 1$
$S_n = n * (2 * n + 1 + 3) / 2 = n * (n + 2)$
所以 $\le N$ 的最大n就是延伸的行数

计算出延伸的行数后，就可以把沙漏分成上中下三部分打印出来。

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 1000 + 10;
int n,N;
char ch;
int main()
{
	scanf("%d %c",&N,&ch);
	for(int i = 0;i < N;i ++)
		if(2 * i * (i + 2) + 1 > N) 
		{
			n = i - 1;
			break;
		}
	for(int i = n;i >= 1;i --)
	{
		for(int j = 1;j <= n - i;j ++) printf(" ");
		for(int j = 1;j <= i * 2 + 1;j ++) printf("%c",ch);
		printf("\n");
	}
	for(int j = 1;j <= n;j ++) printf(" ");
	printf("%c\n",ch);
	for(int i = 1;i <= n;i ++)
	{
		for(int j = 1;j <= n - i;j ++) printf(" ");
		for(int j = 1;j <= i * 2 + 1;j ++) printf("%c",ch);
		printf("\n");
	}
	printf("%d",N - 2 * n * (n + 2) - 1);
	return 0;
}

1035 插入与归并 (25分)

1035 插入与归并

题目描述

根据维基百科的定义：

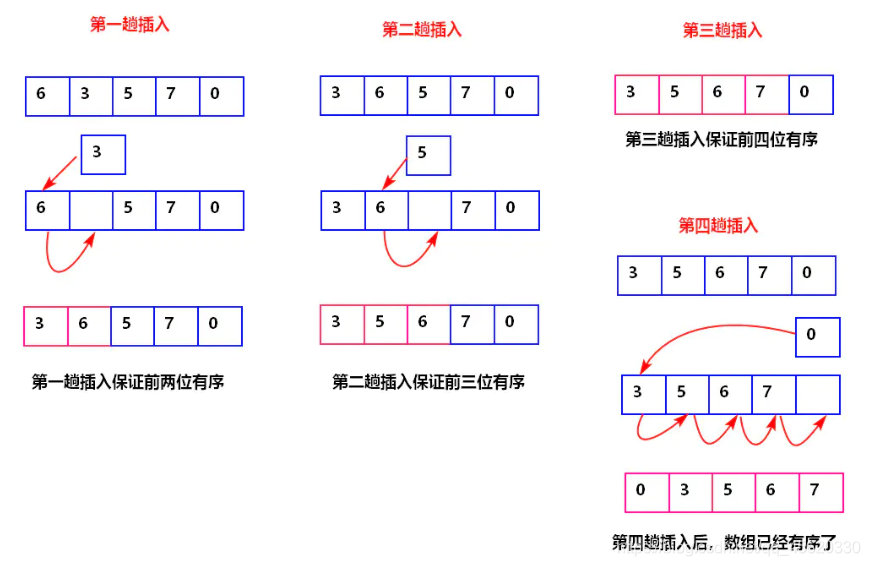
插入排序是迭代算法，逐一获得输入数据，逐步产生有序的输出序列。每步迭代中，算法从输入序列中取出一元素，将之插入有序序列中正确的位置。如此迭代直到全部元素有序。

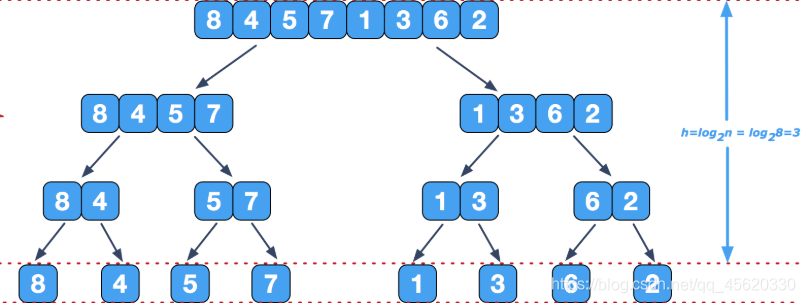
归并排序进行如下迭代操作：首先将原始序列看成 $N$ 个只包含 $1$ 个元素的有序子序列，然后每次迭代归并两个相邻的有序子序列，直到最后只剩下 $1$ 个有序的序列。

现给定原始序列和由某排序算法产生的中间序列，请你判断该算法究竟是哪种排序算法？

输入格式：

输入在第一行给出正整数 $N$ ( $\le100$ )；随后一行给出原始序列的 $N$ 个整数；最后一行给出由某排序算法产生的中间序列。这里假设排序的目标序列是升序。数字间以空格分隔。

输出格式：

首先在第 1 行中输出Insertion Sort表示插入排序、或Merge Sort表示归并排序；然后在第 2 行中输出用该排序算法再迭代一轮的结果序列。题目保证每组测试的结果是唯一的。数字间以空格分隔，且行首尾不得有多余空格。

输入样例 1：

10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0

输出样例 1：

Insertion Sort
1 2 3 5 7 8 9 4 6 0

输入样例 2：

10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6

输出样例 2：

Merge Sort
1 2 3 8 4 5 7 9 0 6

Solution

插入排序
在这里插入图片描述
将无序的数列中第一个元素与有序数列的元素从后到前比较，找到插入位置，将该元素插入到有序数列的适当位置。
在此题中，若给定的中间序列符合前半部分有序，后半部分与初始序列相同，则为插入排序，否则为归并排序。

归并排序
在这里插入图片描述
归并排序的思想就是分治再合并。

如果是插入排序，就把无序序列的第一位和有序序列排一下序，输出即可。
如果是归并排序，就对初始序列模拟一下归并排序的过程，当达到中间序列时，在归并一步即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 100 + 5;
int n,a[SZ],b[SZ];

inline bool check()
{
	for(int i = 2;i <= n;i ++)
	{
		if(b[i] < b[i - 1]) 
		{
			for(int j = i;j <= n;j ++)
			{
				if(b[j] != a[j]) return 0;
			} 
			sort(b + 1,b + i + 1);
			return 1;
		}
	}	
}
int main()
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
	for(int i = 1;i <= n;i ++) scanf("%d",&b[i]);
	if(check())
	{
		printf("Insertion Sort\n");
		for(int i = 1;i <= n;i ++) printf("%d%c",b[i],i == n ? '\n' : ' ');
	}
	else 
	{
		printf("Merge Sort\n");
		int k = 1,flag = 1;
		while(flag)
		{
			flag = 0;
			for(int i = 1;i <= n;i ++)
				if(a[i] != b[i]) flag = 1;
			k <<= 1;
			for(int i = 1;i <= n / k;i ++) sort(a + (i - 1) * k + 1,a + i * k  + 1);
			sort(a + n / k * k + 1,a + n + 1);
		}
		for(int i = 1;i <= n;i ++) printf("%d%c",a[i],i == n ? '\n' : ' ');
	}
}

1040 有几个PAT (25分)

1040 有几个PAT

题目描述

字符串 APPAPT 中包含了两个单词 PAT，其中第一个 PAT 是第 2 位§，第 4 位(A)，第 6 位(T)；第二个 PAT 是第 3 位§，第 4 位(A)，第 6 位(T)。

现给定字符串，问一共可以形成多少个 PAT？

输入格式：

输入只有一行，包含一个字符串，长度不超过 $10^5$ ，只包含 P、A、T 三种字母。

输出格式：

在一行中输出给定字符串中包含多少个 PAT。由于结果可能比较大，只输出对 1000000007 取余数的结果。

输入样例：

APPAPT

输出样例：

Solution

首先对于每一个A，我们只要计算它前面的P的数量和后面的T的数量的乘积，就是这个A对答案的贡献，所有A对答案的贡献即为答案。所以我们对每个A统计一下它前面的P的数量，然后再扫一遍序列，如果出现A,就把当前总的PA组合的数量记录，每出现一个T，形成了PAT，就把当前的PA组合的数量加入答案中去，最终扫完整个序列，即可求得答案。

注意：中间取余，而不是最后取余，防止爆int。

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 1e5 + 20;
const int MOD = 1e9 + 7;
typedef long long ll; 
int prep[SZ];
char s[SZ];

int main()
{
	scanf("%s",s);
	int nump = 0;
	for(int i = 0;i < strlen(s);i ++)
	{
		if(s[i] == 'P') nump ++;
		if(s[i] == 'A') prep[i] = nump;
	}	
	ll ans = 0,sum = 0;
	for(int i = 0;i < strlen(s);i ++)
	{
		if(s[i] == 'A') sum = (sum + prep[i]) % MOD;
		if(s[i] == 'T') ans = (ans + sum) % MOD;
	}
	printf("%lld\n",ans);
	return 0;
}

1045 快速排序 (25分)

1045 快速排序

题目描述

著名的快速排序算法里有一个经典的划分过程：我们通常采用某种方法取一个元素作为主元，通过交换，把比主元小的元素放到它的左边，比主元大的元素放到它的右边。给定划分后的 $N$ 个互不相同的正整数的排列，请问有多少个元素可能是划分前选取的主元？

例如给定 $N = 5$ , 排列是 $1 、 3 、 2 、 4 、 5$ 。则：

$1$ 的左边没有元素，右边的元素都比它大，所以它可能是主元；
尽管 $3$ 的左边元素都比它小，但其右边的 $2$ 比它小，所以它不能是主元；
尽管 $2$ 的右边元素都比它大，但其左边的 $3$ 比它大，所以它不能是主元；
类似原因， $4$ 和 $5$ 都可能是主元。
因此，有 $3$ 个元素可能是主元。

输入格式：

输入在第 $1$ 行中给出一个正整数 N（ $\le$ $10^5$ ）；第 $2$ 行是空格分隔的 $N$ 个不同的正整数，每个数不超过 $10^9$ 。

输出格式：

在第 $1$ 行中输出有可能是主元的元素个数；在第 $2$ 行中按递增顺序输出这些元素，其间以 $1$ 个空格分隔，行首尾不得有多余空格。

输入样例：

5
1 3 2 4 5

输出样例：

3
1 4 5

Solution

对于一个序列，如果当前数字是主元，比它小的数都在它前面，比它大的数都在他后面，那么排序后的序列中该数字的位置不变。
但是仅仅这样并不能判断它一定是主元，例如
$32145$
$12345$
2的位置没有发生改变，但是2前面有比它大的3，所以我们只要再判断一下当前数字是已出现数字中最大的一个即可，这样也就保证了他前面的都是比它小的，也就保证了后面的都比它大。

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 1e5 + 10;
int n,num[SZ],temp[SZ];

int main()
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i ++) 
	{
		scanf("%d",&num[i]);
		temp[i] = num[i];
	}
	sort(temp + 1,temp + n + 1);
	vector<int> vec;
	int maxn = 0;
	for(int i = 1;i <= n;i ++)
	{
		maxn = max(maxn,num[i]);
		if(num[i] == temp[i] && maxn == num[i]) vec.push_back(num[i]);
	} 
	int N = vec.size();
	printf("%d\n",N);
	for(int i = 0;i < N;i ++)
		if(i != N - 1)	printf("%d ",vec[i]);
		else printf("%d",vec[i]);
	printf("\n");
	return 0; 
}

1050 螺旋矩阵 (25分)

1050 螺旋矩阵

题目描述

本题要求将给定的 $N$ 个正整数按非递增的顺序，填入“螺旋矩阵”。所谓“螺旋矩阵”，是指从左上角第 $1$ 个格子开始，按顺时针螺旋方向填充。要求矩阵的规模为 $m$ 行 $n$ 列，满足条件： $m \times n$ 等于 $N$ ； $\ge n$ ；且 $m - n$ 取所有可能值中的最小值。

输入格式:

输入在第 $1$ 行中给出一个正整数 $N$ ，第 $2$ 行给出 $N$ 个待填充的正整数。所有数字不超过 $10^4$ ，相邻数字以空格分隔。

输出格式：

输出螺旋矩阵。每行 $n$ 个数字，共 $m$ 行。相邻数字以 $1$ 个空格分隔，行末不得有多余空格。

输入样例：

12
37 76 20 98 76 42 53 95 60 81 58 93

输出样例：

Solution

枚举找出 $m$ 和 $n$ （或者用一点简单的数学知识优化一下）
利用while循环蛇形填数。

代码

#include<bits/stdc++.h>
using namespace std;
const int SZ = 1e5 + 5; 
int num[SZ],mp[10005][1005];
/*bool cmp(int a,int  b) 
{
   return a>b;
}*/
int main()
{
    int N,m,n;
    scanf("%d",&N);
    
   	/*int temp = 0x3f3f3f3f;
	for(int i = N;i >= 1;i --)
   	{
   		if(N % i == 0) 
   		{
   			if(i >= N / i)
   			{
   				if(i - N / i < temp)
				{
					n = N / i;
					m = i;
					temp =  i - N / i;	
				} 
   			}
   			else break;
   		}
   	}*/
   	for(int i = 1;i * i <= N;i ++)
   	{
		if(N % i == 0)
		{
			n = i;
			m = N / i; 
		}   		
   	}
    
	for(int i = 1;i <= N;i ++)
    scanf("%d",&num[i]);
    sort(num + 1,num + N + 1,greater<int>());
    
	int cnt = 0,line = 1,row = 0;
    while(cnt < N) 
    { //写法上先判断是否越界
        while(row + 1 <= n && !mp[line][row + 1])
            mp[line][++ row] = num[++ cnt];
        while(line + 1 <= m && !mp[line + 1][row])
            mp[++ line][row] = num[++ cnt];
        while(row - 1 > 0 && !mp[line][row - 1])
            mp[line][-- row] = num[++ cnt];
        while(line - 1 > 0 && !mp[line - 1][row])
            mp[-- line][row] = num[++ cnt];   
    }
    
    for(int i = 1;i <= m;i ++)
	{
		for(int j = 1;j <= n;j ++)
			printf("%d%c",mp[i][j],j == n ? '\n' : ' ');
	} 
	return 0;
}

1089 狼人杀-简单版 (20分)

1089 狼人杀-简单版

题目描述

以下文字摘自《灵机一动·好玩的数学》：“狼人杀”游戏分为狼人、好人两大阵营。在一局“狼人杀”游戏中， $1$ 号玩家说：“ $2$ 号是狼人”， $2$ 号玩家说：“ $3$ 号是好人”， $3$ 号玩家说：“ $4$ 号是狼人”， $4$ 号玩家说：“ $5$ 号是好人”， $5$ 号玩家说：“ $4$ 号是好人”。已知这 $5$ 名玩家中有 $2$ 人扮演狼人角色，有 $2$ 人说的不是实话，有狼人撒谎但并不是所有狼人都在撒谎。扮演狼人角色的是哪两号玩家？

本题是这个问题的升级版：已知 $N$ 名玩家中有 $2$ 人扮演狼人角色，有 $2$ 人说的不是实话，有狼人撒谎但并不是所有狼人都在撒谎。要求你找出扮演狼人角色的是哪几号玩家？

输入格式：
输入在第一行中给出一个正整数 $\le N \le 100）$ 。随后 $N$ 行，第 $i$ 行给出第 $i$ 号玩家说的话 $\le i \le N)$ ，即一个玩家编号，用正号表示好人，负号表示狼人。

输出格式：

如果有解，在一行中按递增顺序输出 $2$ 个狼人的编号，其间以空格分隔，行首尾不得有多余空格。如果解不唯一，则输出最小序列解 —— 即对于两个序列 $A = a [1], . . ., a [M]$ 和 $B = b [1], . . ., b [M]$ ，若存在 $\le k < M$ 使得 $\le k）$ ，且 $a [k + 1] < b [k + 1]$ ，则称序列 $A$ 小于序列 $B$ 。若无解则输出 No Solution。

输入样例 1：

5
-2
+3
-4
+5
+4

输出样例 1：

1 4

输入样例 2：

6
+6
+3
+1
-5
-2
+4

输出样例 2（解不唯一）：

1 5

输入样例 3：

5
-2
-3
-4
-5
-1

输出样例 3：

No Solution

Solution

既然狼人和说谎的人的数量是一定的，而且仅有2个,那么不妨直接枚举狼人（或者枚举说谎的人）来判断该情况是否合法。

代码

#include <bits/stdc++.h>
using namespace std;
const int SZ = 100 + 10;
struct zt
{
	char a;
	int b;
}peo[SZ];
int n;

inline bool check(int a,int b)
{
	vector<int> liar; 
	for(int i = 1;i <= n;i ++)
	{
		if(peo[i].a == '+' && (peo[i].b == a || peo[i].b == b)) liar.push_back(i);
		if(peo[i].a == '-' && peo[i].b != a && peo[i].b != b) liar.push_back(i);
	}
	if(liar.size() != 2) return 0;
	int liarnum = 0;
	for(auto x: liar)
		if(x == a || x == b) liarnum ++;
	if(liarnum != 1) return 0;
	return 1;
} 

int main()
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i ++) 
	{
		getchar();
		scanf("%c%d",&peo[i].a,&peo[i].b);
	}
	bool flag = 0;
	for(int i = 1;i < n;i ++) //枚举狼 
	{
		for(int j = i + 1;j <= n;j ++)
		{
			if(check(i,j))
			{
				printf("%d %d\n",i,j);	
				flag = 1;
				break;
			}
		}
		if(flag == 1) break;
	}
	if(!flag) printf("No Solution\n");
	return 0;
}

1094 谷歌的招聘 (20分)

1094 谷歌的招聘

题目描述

2004 年 7 月，谷歌在硅谷的 101 号公路边竖立了一块巨大的广告牌（如下图）用于招聘。内容超级简单，就是一个以 .com 结尾的网址，而前面的网址是一个 $10$ 位素数，这个素数是自然常数 $e$ 中最早出现的 $10$ 位连续数字。能找出这个素数的人，就可以通过访问谷歌的这个网站进入招聘流程的下一步。
自然常数 $e$ 是一个著名的超越数，前面若干位写出来是这样的：
$e = 2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427427466391932003059921 . . .$ 其中粗体标出的 $10$ 位数就是答案。

本题要求你编程解决一个更通用的问题：从任一给定的长度为 $L$ 的数字中，找出最早出现的 $K$ 位连续数字所组成的素数。

输入格式：

输入在第一行给出 $2$ 个正整数，分别是 $L$ （不超过 $1000$ 的正整数，为数字长度）和 $K$ （小于 $10$ 的正整数）。接下来一行给出一个长度为 $L$ 的正整数 $N$ 。

输出格式：

在一行中输出 $N$ 中最早出现的 $K$ 位连续数字所组成的素数。如果这样的素数不存在，则输出 $404$ 。注意，原始数字中的前导零也计算在位数之内。例如在 $200236$ 中找 $4$ 位素数， $0023$ 算是解；但第一位 $2$ 不能被当成 $0002$ 输出，因为在原始数字中不存在这个 $2$ 的前导零。

输入样例 1：

20 5
23654987725541023819

输出样例 1：

输入样例 2：

10 3
2468024680

输出样例 2：

Solution

将字符串处理成整数，然后O（ $\sqrt{n}$ ）判断是否为素数。
注意输出的时候直接输出字符，防止漏掉前导0。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int SZ = 1e3 + 20;
char s[SZ];

inline bool check(int x)
{
	if(x == 0 || x == 1) return 0;
	for(int i = 2;i * i <= x;i ++)
		if(x % i == 0) return 0; 
	return 1;
}

int main()
{
	int n,k;
	ll sum;
	scanf("%d%d",&n,&k);
	scanf("%s",s);
	bool flag = 0;
	for(int i = 0;i < n - k + 1; i ++)
	{	
		sum = 0;
		for(int j = i;j <= i + k - 1;j ++)
		{
			sum = sum * 10 + (s[j] - '0'); 
		}
		if(check(sum)) 
		{
			for(int j = i;j <= i + k - 1;j ++) printf("%c",s[j]);
			printf("\n");
			flag = 1;
			break;
		}
	}
	if(!flag) printf("404");
 	return 0;
}

2020.7.18

PAT 乙级讲题记录

悦读