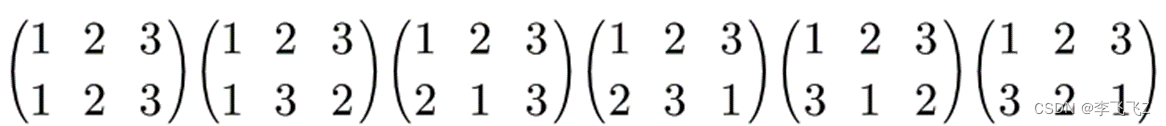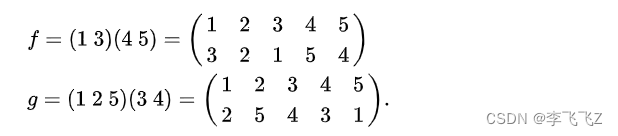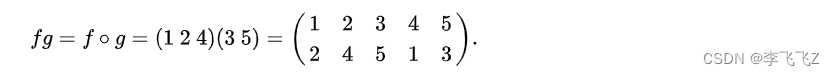1.
在群论中,对称群通常表示为Sₙ,其中 n 是集合中元素的个数。对称群 Sₙ 包含了集合 {1, 2, ..., n} 上所有可能的置换。就是说给定一个集合A,存储 n 个元素,Sₙ 中存储的是这 n 个元素的不同排列。( S 就是Symmetric 的首字母)
例如,S₃ 包含以下六个置换:
- 恒等变换:(1)(2)(3)
- 两个元素的交换:(1 2), (1 3), (2 3)
- 循环置换:(1 2 3)、(1 3 2)
下面这种表示容易理解,上面的例子是更简洁的循环表示法。
假设
g
是置换
(1 3 2)
(表示
1→3,3→2,2→1
),它的逆置换是
g
−
1=(3 2 1)
。我们可以验证:
g
∘
g
−1=(132)∘(321)=(1→3→2→1)=(123)=
e
2.
再有就是:
排列f和g的组成f∘g,发音为“f of g”,
在g 之后应用f首先将1映射到2,然后将2映射到自身;2到5,然后到4;3到4,然后到5,依此类推。所以f和g的组合给出
就是说函数组合是从右向左的
3.
参考:
这个笔记很好,直观的给出了定义:
https://whzecomjm.com/p/2020/07/symmetric-groups-notes/Symmetric-Groups.pdf
这个说的不错:
【群论入门】(10): 排列与对称群 - 知乎 (zhihu.com)
比较官方:
(中文)
https://zh.wikipedia.org/wiki/%E5%AF%B9%E7%A7%B0%E7%BE%A4_(n%E6%AC%A1%E5%AF%B9%E7%A7%B0%E7%BE%A4)
或是
(英文)