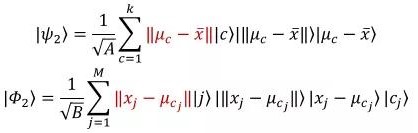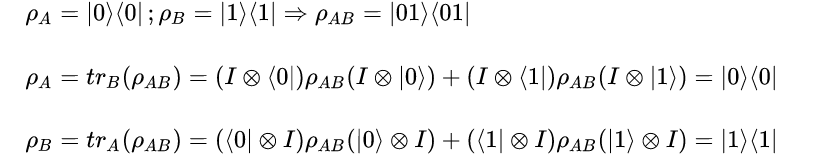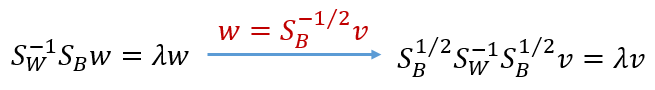前不久的线性判别分析学习过程还历历在目，转瞬间，量子判别分析的学习任务却“接踵而来”，正所谓趁热打铁，在原有的LDA基础上深入了解基于量子计算的QLDA是如何加速算法，相对来说也会更为“简单”。

一 . 前情回顾

前一期博客中，我们从感性分析到理性推导，从图像理解到代码实现，非常详细的介绍了线性判别分析的前因后果，在正式进入量子判别分析算法的学习之前，温故而知新：

LDA考虑的问题是: 对于一个多类别的分类问题，把输入数据的特征空间从高维映射到低维空间中，从而达到降维的目的。为了能够服务于后续的分类任务，LDA希望能够尽可能的保留类判别信息，即希望在原始高维空间中属于一类的数据在低维空间中也属于一类；原始高维空间中属于不同类别的数据在低维空间中也属于不同的类别。上述要求可以通过数据间的“距离”来衡量，即希望类别内的数据点“离的很近”，类别之间“离的很远”，这样两个类别就会越好区分.
具体的推导过程，我们这里也给出了图片：

其中，整个算法的核心就是求出类内散度矩阵和类间散度矩阵，并分别最小化和最大化这二者，之后扫尾工作只需要线性代数的基本水平即可；

二 . QLDA 步骤

与前面介绍的量子算法相同，例如Grover算法，HHL算法，量子LDA的目标是为了加速经典LDA算法。与经典LDA算法相比，量子LDA在训练向量个数M和特征空间维度N上达到了指数级加速效果，极大的减小了计算难度和空间利用率。

本算法的主要过程大致分四步，前期数据处理和均值等基本属性的计算还是基于传统计算机算法，这里我也是在论文中总结而来，有可能不是非常恰当：

1. 利用量子寄存器和 $Oracles$ 算子，记录数据并构建类间散度矩阵 $S_B$ 和类间散度矩阵 $S_w$ 。
2. 将原始特征方程求解问题转换一下，为后期利用相位估计算法求特征值和特征向量做铺垫，所以构建$S_B^{1/2}{S}_W^{-1}{S}_B^{1/2}$。
3. 利用$S_B^{1/2}{S}_W^{-1}{S}_B^{1/2}$ 取幂，执行相位估计算法以获取前 $p$ 个较为重要的特征值和特征向量。
4. 计算$w_r=S_B^{-1/2}{v}_r$。

1. 构建相关矩阵

第一步，我们需要处理数据，新建一种利于量子计算的新型数据存储形式，根据前面的介绍，第一个关键点就是寻找并确定类内矩阵和类间矩阵，这里想强调的是，传统的机器学习算法和其对应的量子机器学学习算法不同的地方就在于优化和提速，本质上数学原理还是共同的，所以传统的LDA有的步骤，在量子判别分析里面是一个也不能少。

本着执果索因的法子，我们先列出目标矩阵：
$$\begin{gathered} S_w=\sum _{c=1}^k(x-{\mu }_c)(x-{\mu }_c{)}^T \\ {S}_B=\sum _{c=1}^k({\mu }_c-\overline{x})({\mu }_c-\overline{x}{)}^T \end{gathered}$$

世界起源于假设，所以假设有$M$个输入数据向量，且每个数据向量有$k$个类，其中每个类中数据均值用 ${\mu }_c$ 来表示，而所有数据向量的均值用 $\overline{x}$ 表示。

曾记否，在$Grover$算法中，灵魂算子$O$将索引目标和其他指标区别开，这里很巧，也用到了大$O$算子，但此$O$非彼 $O$，这里借助量子寄存器$RAM$和$O$算子来存储原始数据。

根据类内矩阵和类间矩阵的表达方式，这里需要存储的数据为
$$\begin{gathered} d_c=x_j-{\mu }_{c_j} \\ {D}_c={\mu }_c-\bar{x} \end{gathered}$$
接下来就是将他们放在$RAM$中，即通过$Oracles$算子：

具体是啥样的呢？我特地画了一张图解释：

基于上述假设，我们可以构建二者的密度矩阵：
$$\begin{array}{c}|{\psi }_1⟩=O_2\left(\frac{1}{\sqrt{k}}{\sum }_{c=1}^k|c⟩|0⟩|0⟩\right)=\frac{1}{\sqrt{k}}{\sum }_{c=1}^k|c⟩|\Vert {\mu }_c-\bar{x}\Vert ⟩|{\mu }_c-\bar{x}⟩\\ |{\Phi }_1⟩=O_1\left(\frac{1}{\sqrt{M}}{\sum }_{j=1}^M|j⟩|0⟩|0⟩|0⟩\right)=\frac{1}{\sqrt{M}}{\sum }_{j=1}^M|j⟩|\Vert x_j-{\mu }_{c_j}\Vert ⟩|x_j-{\mu }_{c_j}⟩|c_j⟩\end{array}$$

其实这一步可以理解为对多个相同维度，数据不同的已初始化好的量子寄存器进行求和而已，其中的$k$代表类别个数，$M$代表一个类中数据个数。

接下来再将上述公式中的基态提取概率幅：

其中这里的$A={\sum }_{c=1}^k{\Vert {\mu }_c-\bar{x}\Vert }^2,B={\sum }_{j=1}^M{\Vert x_j-{\mu }_{c_j}\Vert }^2$

下面就是最重要的一步，通过对密度矩阵求偏迹得到我们想要的散度矩阵，但在这之前，而我们简单理解一下偏迹运算的原理：

它的主要作用就是“复合”和“分离”，假设最简单的两个量子态如下：

是不是非常的清晰明了？再回到刚才的话题，上述两个态构成的密度矩阵执行偏迹运算之后的得到：
$$\begin{gathered} S_B=\frac{1}{A}\sum _{c=1}^k{\Vert {\mu }_c-\bar{x}\Vert }^2|{\mu }_c-\bar{x}⟩⟨{\mu }_c-\bar{x}| \\ {S}_W=\frac{1}{B}\sum _{c=1}^k\sum _{i\in c}{\Vert x_i-{\mu }_c\Vert }^2|x_i-{\mu }_c⟩⟨x_i-{\mu }_c| \end{gathered}$$

构造矩阵就算是大功告成了，我们可以简单总结一下它是如何得到这两个目标散度矩阵的：首先假设数据存储在QRAM中，通过$)Oracle$能够获取$QRAM$中的值存到相应的量子态中；然后提取我们量子态中我们需要的数据至相应的概率幅中；最后执行偏迹运算便可得到最终的$S_B$ 和$S_W$。

2. 化简与特征方程求解

在得到我们想要的类内矩阵和类间散度矩阵之后，正所谓不忘初心，回到问题最开始的地方，我们想求的是啥？是一个方向，一个能够使得样本点在类内间距最小，类间间距最大的一个方向，方向怎么求？线性代数告诉我们使用特征方程可以求得向量的方向！所以，此时的症结应当是特征方程的求解！

由于这个数据量的巨大，用一般的方法去求解一个高阶数的特征方程不会特别的高校，这个时候，前面抓耳挠腮铺垫的相位估计算法就起到了大作用。

熟悉量子相位估计算法的小伙伴就会知道，它也叫作量子特征值估计算法，对于给定的一个$U$ 矩阵和量子态$|\psi ⟩$，量子力学基础告诉我们$U$矩阵的特征值为$e^{2\pi i\theta }$，即$U|\psi ⟩=e^{2\pi i\theta }|\psi ⟩$，这里的$\theta$就是我们的相位，知道了相位，也就知道了特征值，就知道了特征向量。。。就没了。

在这之前，我们需要对原始问题进行转化：

这里千万别懵，前面的式子只是我们传统LDA的结果之一，这里只是用了线代的办法把它变成$Hermitian$矩阵，满足相位估计的输入算法的需求：即构建密度矩阵$S_B^{1/2}{S}_W^{-1}{S}_B^{1/2}$，但是更一般的情况下，不止两个矩阵，可能换元就不是特别的方便了，所以作者又提供了一种更一般的求解方法，这也是论文作者的创新之处了，他利用了一种叫Hermitian chain product的算法来实现该矩阵的构造！

它的主要表达形式如下：
$$\left[f_k\left(A_k\right)\cdots f_1\left(A_1\right)\right]{\left[f_k\left(A_k\right)\cdots f_1\left(A_1\right)\right]}^{†}$$

这里的$A_1,\dots A_k$是已经归一化的半正定厄米矩阵，函数$f_1,\dots f_k$ 是用收敛的泰勒级数表示的，除此之外，还需设定 { λ j l } l = 1 N \left\{\lambda_{j l}\right\}_{l=1}^{N} {λjl​}l=1N​ 为矩阵$A_j$ 的特征值，那么上述公式的计算时间复杂度在：

$$O\left(\frac{X}{{ϵ}^3}\cdot \sum _{j=1}^k{\kappa }_j^2\cdot \left(\frac{{\max }_l\left|f_1\left({\lambda }_{1l}\right)\right|}{{\min }_l\left|f_1\left({\lambda }_{1l}\right)\right|}\right)\prod _{j=2}^k{\left(\frac{{\max }_l\left|f_j\left({\lambda }_{jl}\right)\right|}{{\min }_l\left|f_j\left({\lambda }_{jl}\right)\right|}\right)}^2\right)$$

其中$O(X)$ 代表构造一个符合条件矩阵的时间复杂度，${\kappa }_j^2$ 是矩阵$A_j$ 的最大特征值与其最小特征值的比值。

从这里我们可以得到，此步骤与传统LDA构造矩阵相比为$QLDA$提供了指数加速的效果！

那么基于这里理论，为了构造矩阵$S_B^{1/2}{S}_W^{-1}{S}_B^{1/2}$，只需令$$A_1=S_W,A_2=S_B,f_1(X)=X^{-1/2},f_2(X)=X^{1/2}$$

再代入上面的链积公式即可！

3. 收尾

接下来的主要收尾工作就是寻找到主特征向量，它需要先对$S_B^{1/2}{S}_W^{-1}{S}_B^{1/2}$矩阵进行取幂操作，为了避免矩阵的极小特征值所消耗的时空资源，采用预先定义的条件数进行约束，即假设一个有效的条件数 ${\kappa }_{\mathrm{e}\mathrm{f}\mathrm{f}}$，使得在$\left[1/{\kappa }_{\mathrm{e}\mathrm{f}\mathrm{f}},1\right]$之内的特征值才被我们采用。

通过QPCA中的取幂运算和相位估计，这一步可以得到：

借此得到前$p$个特征值对应的特征向量$v_r$.

再令$A_1=v_r,A_2=S_B,f_1(X)=X,f_2(X)=X^{-1/2}$，代入公式$\left[f_k\left(A_k\right)\cdots f_1\left(A_1\right)\right]{\left[f_k\left(A_k\right)\cdots f_1\left(A_1\right)\right]}^{†}$可以得到QLDA降维算法的目标映射矩阵$w_r=S_B^{-1/2}{v}_r$。也就自然确定了我们投影的方向了！

本期的博客学习就到这里，后期如果有代码的话也会积极的为大家献上！