逻辑回归
1.基本概念
在前面学习线性回归时,我们知道可以对一组测试数据来进行预测输出,线性回归模型能不能用来解决分类问题呢,答案是否定的,但是我们可以利用线性回归再配合辅助函数来构建分类器。逻辑回归是基于
S
i
g
m
o
i
d
Sigmoid
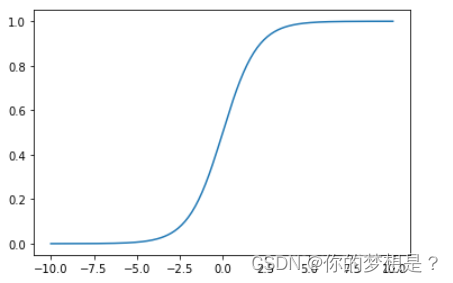
Sigmoid函数,这个函数有很明显的特点。
当
x
x
x>0时,
y
y
y>0.5,
x
x
x<0,时
y
y
y<0.5,并且
y
y
y值在左边区域1,右边趋于0。
S
i
g
m
o
i
d
Sigmoid
Sigmoid公式如下
g
(
z
)
=
1
1
+
e
−
z
(
1.1
)
g(z)=\frac{1}{1+e^{-z}}\quad\quad\quad(1.1)
g(z)=1+e−z1(1.1)
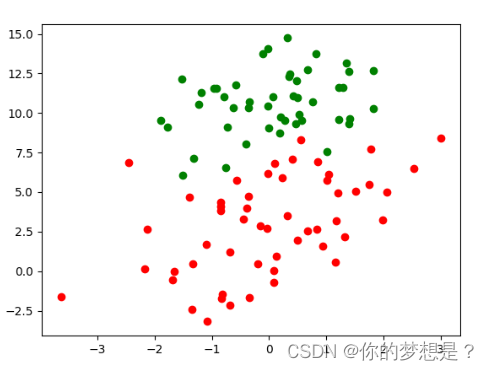
这里有一份已经分好类的数据集,不同颜色代表不同的类别,我么可以很明显的观察到在这两类中间存在这一条分割线,这条线在这里被称作决策边界。我们可以定义这条在决策边界的直线方程为
z
=
f
(
x
(
i
)
)
=
θ
1
x
1
(
i
)
+
θ
2
x
2
(
i
)
+
.
.
.
+
θ
j
x
j
(
i
)
(
1.2
)
z=f(x^{(i)})=\theta_1x_1^{(i)}+\theta_2x_2^{(i)}+...+\theta_jx_j^{(i)}\quad(1.2)
z=f(x(i))=θ1x1(i)+θ2x2(i)+...+θjxj(i)(1.2)
这里我用上标
i
i
i表示第
i
i
i个样本,用
j
j
j表示特征维度。虽然决策边界方程已经确定下来了,但是如何使用决策边界来做分类问题呢,根据我们高中所学的方程思想,在决策边界上的数据点对于1.2式的值会等于0,在决策边界上的数据点对于1.2式会大于0,对于决策边界下的数据点对于1.2式会小于0。若预测z值大于0为1类,z值小于0为0类,这样就很好的解决了二分类问题。目前的问题只需要将z值转化为0/1值
z
=
f
(
x
(
i
)
)
=
θ
T
X
(
1.3
)
z=f(x^{(i)})=\theta^TX\quad\quad\quad(1.3)
z=f(x(i))=θTX(1.3)
其中X是
m
∗
n
m*n
m∗n的矩阵
X
=
[
x
1
(
1
)
x
1
(
2
)
.
.
.
x
1
(
j
)
x
2
(
1
)
x
2
(
2
)
.
.
.
x
2
(
j
)
.
.
.
x
i
(
1
)
x
i
(
2
)
.
.
.
x
i
(
j
)
]
(
1.4
)
X=\begin{bmatrix}x_1^{(1)}&x_1^{(2)}&...&x_1^{(j)}\\x_2^{(1)}&x_2^{(2)}&...&x_2^{(j)}\\.\\.\\.x_i^{(1)}&x_i^{(2)}&...&x_i^{(j)} \end{bmatrix}(1.4)
X=
x1(1)x2(1)...xi(1)x1(2)x2(2)xi(2).........x1(j)x2(j)xi(j)
(1.4)
观察上面的sigmoid辅助函数函数的特性。令p=g(z),它可以将z值转化为一个接近于0或1的p值,
p
=
1
1
+
e
−
z
(
1.5
)
p=\frac{1}{1+e^{-z}}\quad\quad(1.5)
p=1+e−z1(1.5)
根据上式1.5可以将p视为类后验概率估计P(y=1|x),由于类别标签不是1就是0,所以类别0的后验概率也可以得出(此句来自西瓜书p59,目前还未深究)
P
(
y
=
1
∣
x
)
=
p
P
(
y
=
0
∣
x
)
=
1
−
p
(
1.6
)
P(y=1|x)=p\quad\quad\quad P(y=0|x)=1-p\quad(1.6)
P(y=1∣x)=pP(y=0∣x)=1−p(1.6)
将公式1.6一般化
P
(
y
∣
x
)
=
{
p
if
y
=
1
1
−
p
if
y
=
0
(
1.7
)
P(y|x)=\begin{cases} p & \text{if } y = 1 \\ 1-p & \text{if } y = 0 \end{cases} \quad\quad(1.7)
P(y∣x)={p1−pif y=1if y=0(1.7)
分段函数不好计算,继续转换
P
(
y
∣
x
)
=
p
y
(
1
−
p
)
(
1
−
y
)
(
1.8
)
P(y|x)=p^y(1-p)^{(1-y)}\quad\quad(1.8)
P(y∣x)=py(1−p)(1−y)(1.8)
当然只是一个样本的类别后验概率,对于训练数据集中有m个数据样本,采用极大似然法计算整个样本的总后验概率
P
总
=
P
(
y
1
∣
x
1
)
P
(
y
1
∣
x
1
)
.
.
.
P
(
y
m
∣
x
m
)
=
∏
i
=
1
m
P
(
y
i
∣
x
i
)
(
1.9
)
P_总=P(y_1|x_1)P(y_1|x_1)...P(y_m|x_m)\\=\prod_{i=1}^mP(y_i|x_i)\quad\quad(1.9)
P总=P(y1∣x1)P(y1∣x1)...P(ym∣xm)=i=1∏mP(yi∣xi)(1.9)
由于1.9式中连乘容易造成结果下溢,常采用对数似然
l
n
(
P
总
)
=
∑
i
=
1
m
y
i
l
n
(
p
)
+
(
1
−
y
i
)
l
n
(
1
−
p
)
)
(
1.10
)
ln(P_总)=\sum_{i=1}^my_iln(p)+(1-y_i)ln(1-p))\quad(1.10)
ln(P总)=i=1∑myiln(p)+(1−yi)ln(1−p))(1.10)
得到式1.10后,我们就可以开始定义损失函数,损失函数是用来衡量模型预测值与真实值的差距,我们希望这种差距越小越好,式1.10中计算出来的结果是训练集总后验概率的极大似然,我们希望这个概率越大越好,与损失函数理念违背,加个负号后就与损失函数理念相符,所以这里的损失函数定义为
J
(
θ
)
=
−
l
n
(
P
总
)
=
∑
i
=
1
m
−
y
i
l
n
(
p
)
−
(
1
−
y
i
)
l
n
(
1
−
p
)
)
(
1.11
)
J(\theta)=-ln(P_总)=\sum_{i=1}^m-y_iln(p)-(1-y_i)ln(1-p))\quad(1.11)
J(θ)=−ln(P总)=i=1∑m−yiln(p)−(1−yi)ln(1−p))(1.11)
损失函数定义出来后,求解最佳参数的决策边界方程转化求解最佳参数
θ
\theta
θ使得损失函数值最小对这里求解最佳参数方法使用梯度下降法,所谓的梯度就是损失函数对各个参数的偏导向量,其求偏导有
α
J
α
θ
j
=
∑
i
=
1
m
(
p
−
y
i
)
x
i
\frac{\alpha J}{\alpha \theta_j}=\sum_{i=1}^{m}(p-y_i)x_i
αθjαJ=i=1∑m(p−yi)xi
利用线性回归中接受的梯度下降法求解最佳
θ
\theta
θ,其中
β
\beta
β时是学习率
θ
j
n
e
w
=
θ
j
o
l
d
−
β
α
J
o
l
d
α
θ
j
\theta_j^{new}=\theta_j^{old}-\beta\frac{\alpha J^{old}}{\alpha \theta_j}
θjnew=θjold−βαθjαJold
2.代码实现
#导入科学计算包
from numpy import *
#导入matplot第三方包
import matplotlib.pyplot as plt
#读取文本文件,创建数据集
def loadDataSet():
#定义数据集,标签集
dataMat=[]
labelMat=[]
#打开文本文件
f=open("D:/学习资料\机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch05/testSet.txt")
#存储数据集
for line in f.readlines():
lineArr=line.strip().split()
#添加一列全为1的数据
dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat,labelMat
#定义sigmoid函数
def sigmoid(inx):
return 1.0/(1+exp(-inx))
#计算梯度
def get_gent(data,label,theta,m):
return dot(data.T,(sigmoid(dot(data,theta))-label))
#计算损失函数
def get_loss(data,label,theta,m):
var=ones((m,1))
print(shape(var))
return -(label.T*log(sigmoid(dot(data,theta)))+(var-label).T*log(var-sigmoid(dot(data,theta))))
#梯度下降法
def gent_dense(data,label,alpha,epochs):
#获取数据集形状
m,n=shape(data)
# 初始化theta
theta=ones((n,1))
#获取损失值
loss=get_loss(data,label,theta,m)
#定义存储损失值列表
loss_list=list()
# print(loss)
loss_list.append(loss.tolist()[0][0])
# 获取梯度
gent=get_gent(data,label,theta,m)
#迭代
for i in range(epochs):
#获取新的参数
# print(shape(gent))
theta=theta-alpha*gent
#获取梯度
gent=get_gent(data, label, theta, m)
#获取损失值
# print(shape(theta))
loss=get_loss(data,label,theta,m)
loss_list.append(loss.tolist()[0][0])
return theta,loss_list
#绘图
def ploter(data,label,theta,loss_list,epochs):
# # 设置中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(range(epochs+1),loss_list)
plt.xlabel("迭代次数")
plt.ylabel("损失函数值")
plt.show()
fig = plt.figure()
# 创建一个1X1的绘图区域
ax = fig.add_subplot(111)
x1=list()
y1=list()
x2=list()
y2=list()
x3=list()
for i in range(len(data)):
if label[i]==0:
x1.append(data[i][1])
y1.append((data[i][2]))
else:
x2.append((data[i][1]))
y2.append((data[i][2]))
x3=data[i][0]
plt.scatter(x1,y1,color='green')
plt.scatter(x2, y2, color='red')
# 创建一个等距离的一维数组,作为X轴的间隔
x = arange(-3.0, 3.0, 0.1)
# 划分最佳直线方程
print(theta.tolist()[0])
y = (-theta.tolist()[0][0] - theta.tolist()[1][0] * x) / theta.tolist()[2][0]
plt.plot(x,y)
plt.show()
#测试
if __name__=='__main__':
data,label=loadDataSet()
epchos=500
theta,loss_list=gent_dense(mat(data),mat(label).T,0.001,epchos)
print(theta,loss_list)
ploter(data,label,theta,loss_list,epchos)
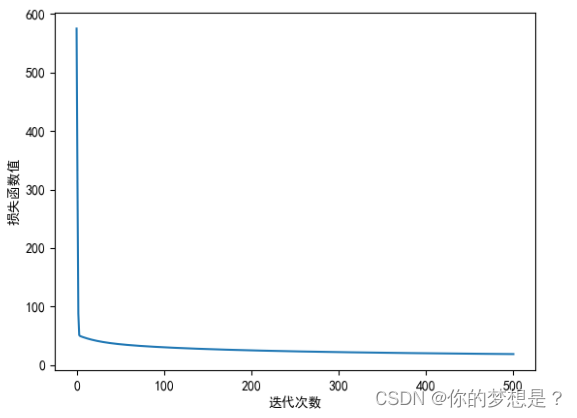
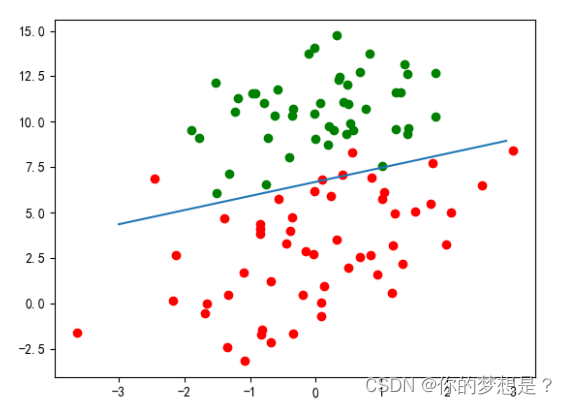
损失函数图像,决策边界拟合图像如下
可以看出仍然有几个点预测错误,但是这个拟合出来的决策边界还是相当可靠的
3.总结
求解最佳参数的方法不止有梯度下降法,还有牛顿法,BFGS等方法。
参考博客:https://zhuanlan.zhihu.com/p/44591359
参考书籍:《机器学习》周志华 《机器学习实战》Peter