SVM线性支持向量机

1.理想态线性可分支持向量机

支持向量机是一种监督学习算法，既可以用来做分类也可以用来做回归。支持向量机一般用来解决二分类问题， y i ∈ { − 1 , 1 } y_i\in\{-1,1\} yi​∈{−1,1}，为了先入门学习支持向量机，先学习线性可分的支持向量机，等掌握明白了线性可分在引入其它问题的支持向量机

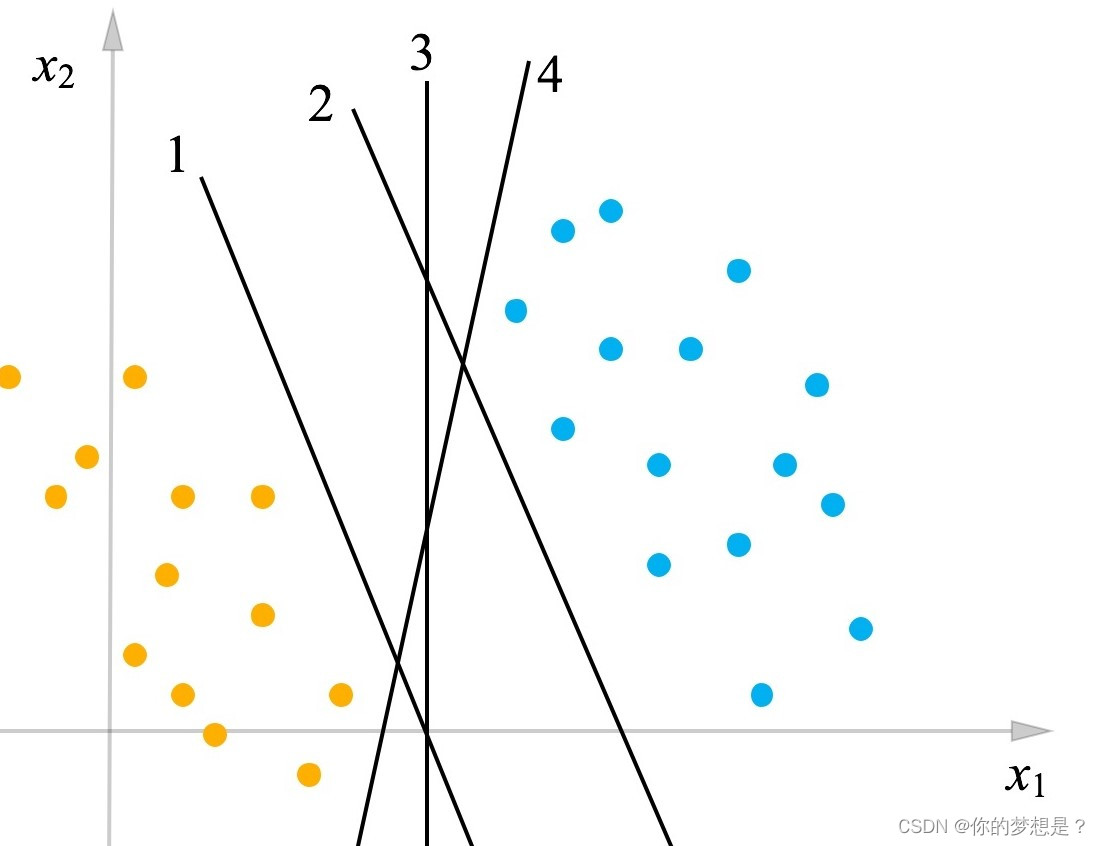
在上图中，蓝色和黄色代表不同的数据点，能够找好多条分隔这两类的数据点，就如图中的4条黑色线条，有这么多条划分的黑线，进一步就会想找一条最优的划分，这个最优在支持向量机中定义为对训练样本的容错性更好，简单的说就是到这两类最近的数据样本距离最大，这条最优的划分黑线被称做划分超平面。通过线性方程定义
$$w^T\ast x+b=0(1.1)$$
$w$是参数，$b$是位移量,根据式1.1划分超平面方程我们就可以做二分类问题了，在超平面上面的数据点代入超平面方程中是大于0的，可以认为是1类，在超平面下方的数据带入超平面方程中是小于0的，可以认为是-1类，那么对于正确分类的数据点有
$$\{\begin{array}{ll}{w}^T{x}_i+b>0& \text{if }y=1\\ w^T{x}_i+b<0& \text{if }y=-1\end{array}(1.2)$$

1.1最佳划分超平面

对于这么多的划分超平面，最佳的划分超平面需要满足在分类正确的情况下找出最小几何间隔最大化的划分超平面，

几何间隔：训练集样本点到划分超平面$w^{T}x+b$的间隔为
$${\gamma }_i=\frac{\left|w^T{x}_i+b\right|}{\left|\left|w\right|\right|}(1.3)$$
由于划分超平面需要满足分类正确，根据式1.2在分类正确的情况下
$$y_i\ast (w^T{x}_i+b)>0(1.4)$$
利用式1.4可以把式1.3绝对值去掉（yi要么是1要么是-1，式1.3乘上yi不会对计算几何间隔产生影响）
$${\gamma }_i=\frac{y_i(w^T{x}_i+b)}{\left|\left|w\right|\right|}(1.5)$$
几何间隔的最小值的数据点就是所谓的支持向量
$$\gamma =mi{n}_i{\gamma }_i=mi{n}_i\frac{y_i(w^T{x}_i+b)}{\left|\left|w\right|\right|}(1.6)$$
最小几何间隔最大化用公式描述为
$$ma{x}_{(w,b)}mi{n}_i{\gamma }_i(1.7)$$
对式1.5进一步变形
$${\gamma }_i=y_i(\frac{w^T}{\left|\left|w\right|\right|}\ast x_i+\frac{b}{\left|\left|w\right|\right|})(1.8)$$
对于式1.8，yi和xi都是已知的样本点，只有参数w,b是未知的，再结合式1.7的描述就可以将找到最佳划分超平面转的问题转化为求解最佳参数w,b的新问题
新问题： m a x ( w , b ) γ s . t y i ( w T ∣ ∣ w ∣ ∣ ∗ x i + b ∣ ∣ w ∣ ∣ ) ≥ γ i ∈ { 1 , 2.. m } ( 1.9 ) 新问题：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\max(w,b)\gamma\\s.t\quad y_i(\frac{w^T}{\left|\left|w\right|\right|}*x_i+\frac{b}{\left|\left|w\right|\right|})\geq\gamma\quad i\in\{1,2..m\}\quad(1.9) 新问题：max(w,b)γs.tyi​(∣∣w∣∣wT​∗xi​+∣∣w∣∣b​)≥γi∈{1,2..m}(1.9)
其中$\gamma$等于式1.6,其中有m个不等式约束条件，但是这个转化后的问题看上去还是有些复杂,将几何间隔替换成函数间隔，那么最佳划分超平面就是需要在分类正确的情况下找出最小函数间隔最大化的划分超平面

函数间隔：函数间隔与几何间隔之间都能反映数据样本到划分超平面的距离，但是其中存在一些问题，训练样本数据到划分超平面的函数间隔为
$${\hat{\gamma }}_i=\left|w^T{x}_i+b\right|(1.10)$$
划分超平面还需要满足对数据样本分类正确，所以还需满足式1.4的条件，结合式1.10和式1.4，可以把绝对值去掉
$${\hat{\gamma }}_i=y_i(w^T{x}_i+b)(1.11)$$
对于支持向量的函数间隔为
$$\hat{\gamma }=mi{n}_i{\gamma }_i=mi{n}_i{y}_i(w^T{x}_i+b)(1.12)$$
对比支持向量的函数间隔与几何间隔之间的关系，也就是对比式1.6和式1.12发现它们的关系
$$\gamma =\frac{\hat{\gamma }}{\left|\left|w\right|\right|}(1.13)$$
将式1.13代如式1.9中，问题可以转化为
新问题： m a x ( w , b ) γ ^ ∣ ∣ w ∣ ∣ s . t y i ( w T ∗ x i + b ) ≥ γ ^ i ∈ { 1 , 2.. m } ( 1.14 ) 新问题：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\max(w,b)\frac{\hat\gamma}{\left|\left|w\right|\right|}\\s.t\quad y_i(w^T*x_i+b)\geq\hat\gamma\quad i\in\{1,2..m\}\quad(1.14) 新问题：max(w,b)∣∣w∣∣γ^​​s.tyi​(wT∗xi​+b)≥γ^​i∈{1,2..m}(1.14)
对式1.12为了简化问题，可以令支持向量的函数间隔$\hat{\gamma }=1$,为什么要这样简化问题，目前还没有深究为什么会提出这种想法，但是经下面推导令支持向量函数间隔$\hat{\gamma }=1$不会改划分超平面方程，求解问题目标函数，及变约束条件(如果知道为什么的小伙伴请记得留言)对于式1.12将$\hat{\gamma }$换到左边去
$$1=mi{n}_i{y}_i(\frac{w^T}{\hat{\gamma }}\ast x_i+\frac{b}{\hat{\gamma }})(1.15)$$
由于支持向量函数间隔在给定的数据样本中它与最佳划分超平面有关，也就是与参数$w,b$,在给定$w,b$后，$\hat{\gamma }$就是一个常数，有关可以令$\hat{w}=\frac{w^T}{\hat{\gamma }},\hat{b}=\frac{b}{\hat{\gamma }}$经过这样转化后，原来描述最佳超平面的参数$w,b$换成了参数$\hat{w},\hat{b}$,这样同比例的变化最佳划分超平面方程$w^T\ast x+b=0$的参数，划分超平面方程并不会发生改变

再来看看式1.12，当使用$\hat{w}=\frac{w^T}{\hat{\gamma }},\hat{b}=\frac{b}{\hat{\gamma }}$变换参数后，式1.12变化为
新问题： m a x ( w , b ) γ ^ ∣ ∣ w γ ^ ∣ ∣ s . t y i ( w T γ ^ ∗ x i + b γ ^ ) ≥ γ ^ i ∈ { 1 , 2.. m } ( 1.16 ) 新问题：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\max(w,b)\frac{\hat\gamma}{\left|\left|\frac{w}{\hat\gamma}\right|\right|}\\s.t\quad y_i(\frac{w^T}{\hat\gamma}*x_i+\frac{b}{\hat\gamma})\geq\hat\gamma\quad i\in\{1,2..m\}\quad(1.16) 新问题：max(w,b) ​ ​γ^​w​ ​ ​γ^​​s.tyi​(γ^​wT​∗xi​+γ^​b​)≥γ^​i∈{1,2..m}(1.16)
当令$\hat{\gamma }$=1后，式1.14是完全等价的，所以令支持向量函数间隔$\hat{\gamma }=1$

不会改变划分超平面，求解目标函数，及约束条件，对于式1.9的问题可以转化为
新问题： m a x ( w , b ) 1 ∣ ∣ w ∣ ∣ s . t y i ( w T ∗ x i + b ) ≥ 1 i ∈ { 1 , 2.. m } ( 1.17 ) 新问题：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\max(w,b)\frac{1}{\left|\left|w\right|\right|}\\s.t\quad y_i(w^T*x_i+b)\geq1\quad i\in\{1,2..m\}\quad(1.17) 新问题：max(w,b)∣∣w∣∣1​s.tyi​(wT∗xi​+b)≥1i∈{1,2..m}(1.17)
其中$\left|\left|w\right|\right|=\sqrt{w_1^2+w_2^2+...+w_n^2}$,对于式1.13将求最大值转化为求最小值，同时为了后面求导方便还可以添加一个常数项，这对于问题模型求解最佳参数$w,b$并没有发生任何变化
新问题： m i n ( w , b ) 1 2 ∣ ∣ w ∣ ∣ 2 s . t y i ( w T ∗ x i + b ) ≥ 1 i ∈ { 1 , 2.. m } ( 1.18 ) 新问题：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\min(w,b)\frac{1}{2}\left|\left|w\right|\right|^2\\s.t\quad y_i(w^T*x_i+b)\geq1\quad i\in\{1,2..m\}\quad(1.18) 新问题：min(w,b)21​∣∣w∣∣2s.tyi​(wT∗xi​+b)≥1i∈{1,2..m}(1.18)

1.2拉格朗日函数及对偶问题

对于式1.14，这就是支持向量机的基本型，并且属于凸优化问题，为了解决这个凸优化问题，使用拉格朗日乘子法，拉格朗日乘子法能够将一种约束优化问题转化为无约束优化问题

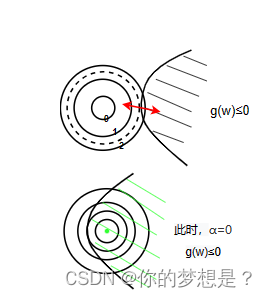
这里使用等高线表示凸函数，在等高线圈内的目标函数值f(w)越来越小，而对于约束条件g(w)$\leq$0在第一幅图情况下，当两个函数图像相切的情况下取得在约束条件下的极小值,此时两个函数的导数值成比例
$$\frac{\partial f}{\partial w}=\alpha \frac{\partial g}{\partial w}(1.19)$$
对于上图中第二种情况下在约束条件下，目标函数值f(w)在取到最小值的时候，此时约束条件g(w)没有起到任何约束作用，可以令式1.19的$\alpha =0$。根据上面两者情况的分析，构造在约束条件下$g(w)\le 0$的拉格朗日函数,其中$\alpha$为拉格朗日乘子,$\alpha \ge 0$
$$minL(w,\alpha )=f(w)-\alpha g(w)(1.20)$$
现在已经简单了解了拉格朗日乘子法，现在可以对式1.14的问题构造拉格朗日目标函数
$$minL(w,b,\alpha )=\frac{1}{2}{\left|\left|w\right|\right|}^2-\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b)){\alpha }_i\ge 0(1.21)$$

其中${\alpha }_i$是各个约束条件的拉格朗日乘子，经过构造拉格朗日函数后，拉格朗日函数中有三个参数，求解参数过程中需要使用对偶问题将求解三个参数问题转化为求解一个参数的问题，式1.18的原始问题为
$$mi{n}_{(w,b)}ma{x}_{\alpha }L(w,b,\alpha )(1.22)$$
其对偶问题是
$$ma{x}_{\alpha }mi{n}_{(w,b)}L(w,b,\alpha )(1.23)$$
根据式1.23的对偶问题先求参数$w,b$使得式1.21内部极小化，式1.21分别对$w,b$求导数并令其等于0
$$\begin{gathered} \partial L_w=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i=0 \\ \partial L_b=-\sum _{i=1}^m{\alpha }_i{y}_i=0(1.24) \end{gathered}$$
将式1.24代入式1.23中将问题转化为求解一个最优参数的目标函数
$$ma{x}_{\alpha }L(\alpha )=ma{x}_{\alpha }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{\alpha }_j{y}_j{x}_i^T{x}_j(1.25)$$
根据式1.25，问题最终转化为在约束条件下求解最优参数$\alpha$使目标函数值最大
m a x α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i y i α j y j x i T x j s . t ∑ i = 1 m α i y i = 0 ( 1.26 ) α i ≥ 0 i ∈ { 1 , 2 , . . . m } max_{\alpha}\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_iy_i\alpha_jy_jx_i^Tx_j\\ s.t\quad\sum_{i=1}^m\alpha_iy_i=0\quad\quad\quad(1.26)\\\alpha_i\geq0\quad i\in\{1,2,...m\} maxα​i=1∑m​αi​−21​i=1∑m​j=1∑m​αi​yi​αj​yj​xiT​xj​s.ti=1∑m​αi​yi​=0(1.26)αi​≥0i∈{1,2,...m}

1.3在约束条件下求解最佳参数

求解出最佳参数$\alpha$有很多种方法，比如后面介绍的SMO最小序列法，如何来求解其它两个参数呢。

注意在原问题转化为对偶问题时需要满足KKT条件
K K T 条件： ∂ ( w , b ) L = 0 α i g ( x i ) = 0 g ( x i ) ≤ 0 ( 1.27 ) α i ≥ 0 i ∈ { 1 , 2 , . . . m } KKT条件：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\\partial_{(w,b)}L=0\\ \alpha_ig(x_i)=0\\g(x_i)\leq0\quad\quad\quad(1.27)\\\alpha_i\geq0\\i\in\{1,2,...m\} KKT条件：∂(w,b)​L=0αi​g(xi​)=0g(xi​)≤0(1.27)αi​≥0i∈{1,2,...m}
参数$w$的求解利用式1.24中第一个式子，其中$x_i,y_i$都是样本数据
$$w=\sum _{i=1}^m{\alpha }_i{x}_i{y}_i(1.28)$$
参数$b$的求解需要利用到KKT条件中的第二个条件
$${\alpha }_{i}g(x_i)={\alpha }_i(1-y_i(w^T\ast x_i+b))=0(1.29)$$
在式1.29中求解出来的最佳参数${\alpha }_i$不可能全部都等于0，这里可以假设如果全部都等于0的话，那么求出来的$w$也就全部都等于0，则最佳超平面方程就是一个常数，显然这是不成立的假设，所以存在不等于0的${\alpha }_i$满足式1.29，则有
$$\begin{gathered} 1-y_i(w^T\ast x_i+b)=0 \\ =>b=y_i-w^T{x}_i=y_i-\sum _{j=1}^m{\alpha }_j{y}_j{x}_j^T{x}_i(1.30) \end{gathered}$$
对于式1.30发现$y_i$不是1就是-1,所以$w^T{x}_i+b=y_i$就是根据对支持向量来求解参数$b$

现在最优的参数$w,b$都可以根据参数$\alpha$求解，但是这里对式1.26求解最优参数$\alpha$的方法先不解释。以上解决的都是理想态的线性可分的支持向量机

2.现实状态的线性可分支持向量机

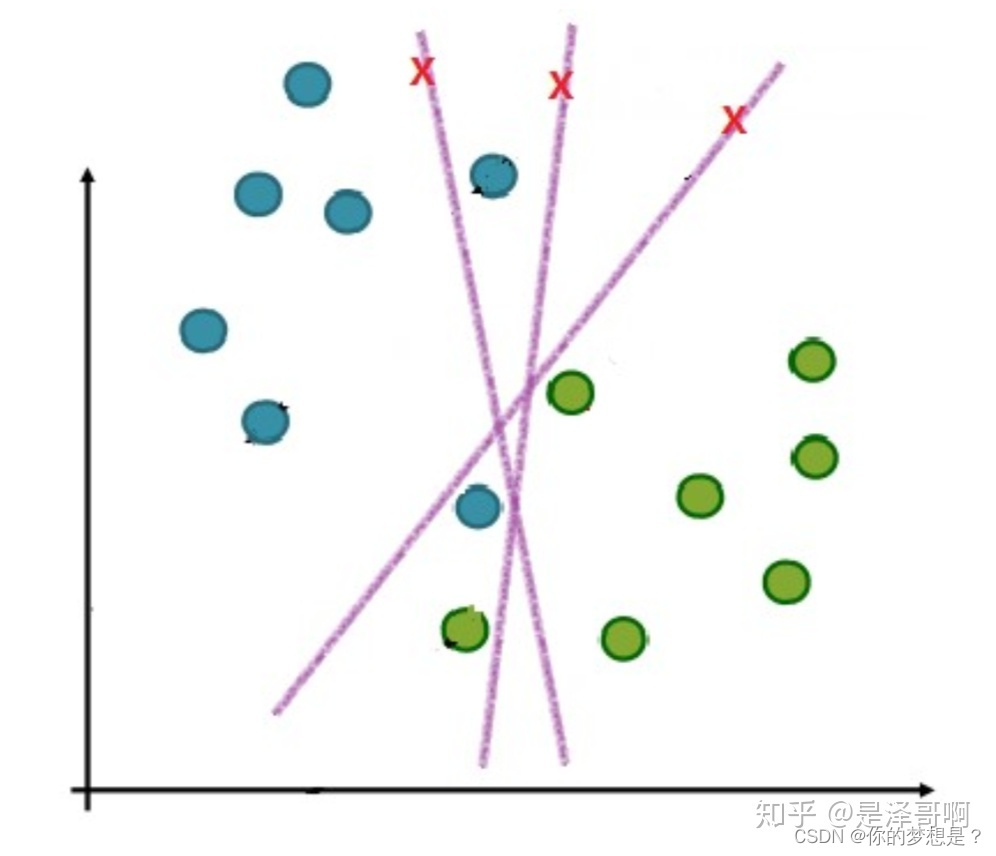
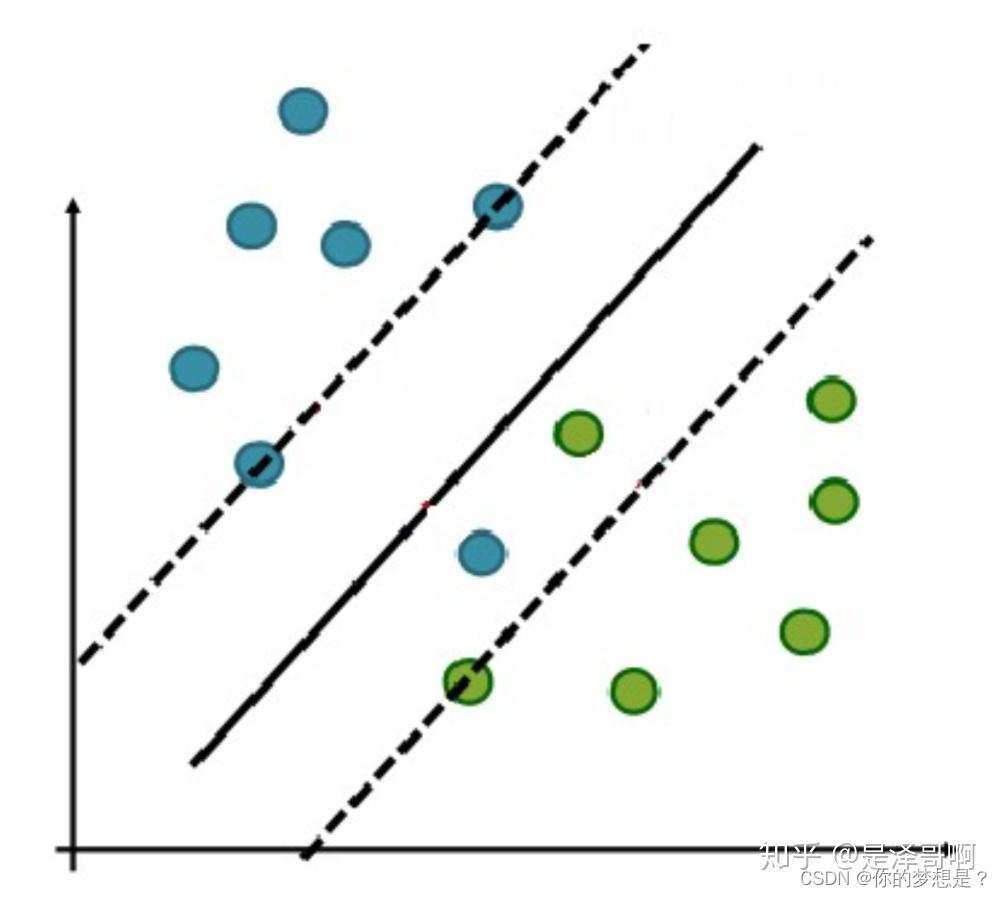
在前面所有的样本数据都式需要满足式1.18的约束条件，这被称为硬间隔，而在现实状态下往往有很多数据样本因为误差或者是噪声的存在并不一定能够满足式1.18的约束条件，那这就很难这要养满足要求的划分超平面进行划分数据集。

在上图中，无论我们如何划分数据样本，都会有一些数据点划分错误，为了解决这个问题，就希望能够容许一些划分错误的数据样本点存在，为此就引入了软间隔，对每一个样本点都指定一个松弛因子${\zeta }_i$

2.1求解加入软间隔后的最优超平面参数

对于在划分间隔外,且分类错误的数据点${\zeta }_i>1$,对于位于划分间隔内的数据点${\zeta }_i\in (0,1)$ 加入松弛化因子${\zeta }_i\ge 0$后,式1.18的约束条件也需要发生更改
$$y_i(w^T{x}_i+b)+{\zeta }_i\ge 1(2.1)$$
为了体现每个样本数据的松弛因子${\zeta }_i$的不一致,还需要引入惩罚因子C,C>0式1.18的问题就转化成
新问题： m i n ( w , b ) 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ i = 1 m ζ i s . t y i ( w T ∗ x i + b ) ≥ 1 i ∈ { 1 , 2.. m } ( 2.2 ) 新问题：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\min(w,b)\frac{1}{2}\left|\left|w\right|\right|^2+C\sum_{i=1}^m\zeta_i\\s.t\quad y_i(w^T*x_i+b)\geq1\quad i\in\{1,2..m\}\quad(2.2) 新问题：min(w,b)21​∣∣w∣∣2+Ci=1∑m​ζi​s.tyi​(wT∗xi​+b)≥1i∈{1,2..m}(2.2)
惩罚因子C越大，${\zeta }_i$就月小，数据样本点在分隔超平面内的弹性空间也就越小。就式2.2构造相应的拉格朗日函数
$$\begin{gathered} minL(w,b,\zeta ,\alpha ,\mu )=\frac{1}{2}{\left|\left|w\right|\right|}^2+C\sum _{i=1}^m{\zeta }_i \\ -\sum _{i=1}^m{\alpha }_i(1-{\zeta }_i-(y_i(w^T{x}_i+b))-\sum _{i=1}^m{\mu }_i{\zeta }_i)(2.3) \\ s.t1-{\zeta }_i-y_i(w^T{x}_i+b)\le 0 \\ -{\zeta }_i\le 0 \end{gathered}$$
式2.3的原始问题为
$$mi{n}_{(w,b,{\zeta }_i)}ma{x}_{(\alpha ,\mu )}L(w,b,\zeta ,\alpha ,\mu )(2.4)$$
对偶问题为
$$ma{x}_{(\alpha ,\mu )}mi{n}_{(w,b,\zeta )}L(w,b,\zeta ,\alpha ,\mu )(2.5)$$
根据式2.5的对偶问题先求参数$w,b,{\zeta }_i$使得式2.3内部极小化，式2.3分别对$w,b,{\zeta }_i$求导数并令其等于0
$$\begin{gathered} \partial L_w=w-\sum _{i=1}^m{\alpha }_i{y}_i{x}_i=0 \\ \partial L_b=-\sum _{i=1}^m{\alpha }_i{y}_i=0(2.6) \\ \partial L_{\zeta }=C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
根据式2.6，可以推出以下关系
$$\begin{gathered} w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i \\ \sum _{i=1}^m{\alpha }_i{y}_i=0(2.7) \\ {\mu }_i=C-{\alpha }_i \end{gathered}$$
将式2.7代入式2.5中，可以将求解多个最优参数的的目标函数转换为只求解一个最优参数的目标函数,这里为了式子看上去简洁，令$x_i^T{x}_j=K_{ij}$
$$\begin{gathered} maxL(\alpha )=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{\alpha }_j{y}_j{K}_{ij}+\sum _{i=1}^m(C-{\alpha }_i-{\mu }_i){\zeta }_i+ \\ \sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{a}_j{y}_j{K}_{ij}-\sum _{i=1}^m{\alpha }_i{y}_{i}b(2.8) \\ =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{y}_i{\alpha }_j{y}_j{K}_{ij} \\ s.t\sum _{i=1}^m{\alpha }_i{y}_i=0{\mu }_i\ge 0{\alpha }_i\ge 0 \end{gathered}$$
式2.8的约束条件看起来有些多，并且出现了不想出现的${\mu }_i$可以结合式2.7的第三个等式将约束条件进一步简化
$$s.t\sum _{i=1}^m{\alpha }_i{y}_i=00\le \alpha \le C(2.9)$$
再将原问题转换成对偶问题时需要满足下面的KKT条件
K K T 条件： ∂ ( w , b , ζ , α , μ i ) L = 0 α i g ( x i ) = 0 μ i ζ i = 0 g ( x i ) ≤ 0 ( 2.10 ) α i ≥ 0 μ i ≥ 0 i ∈ { 1 , 2 , . . . m } KKT条件：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\\partial_{(w,b,\zeta,\alpha,\mu_i)}L=0\\ \alpha_ig(x_i)=0\\\mu_i\zeta_i=0\\g(x_i)\leq0\quad\quad\quad(2.10)\\\alpha_i\geq0\\\mu_i\geq0\\i\in\{1,2,...m\} KKT条件：∂(w,b,ζ,α,μi​)​L=0αi​g(xi​)=0μi​ζi​=0g(xi​)≤0(2.10)αi​≥0μi​≥0i∈{1,2,...m}
再根据式2.8求解出最佳参数$\alpha$后，依次还需要求解出$w,b$的参数，参数$w$可以利用式2.7的第一个等式,其中$x_i,y_i$都是样本数据
$$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i(2.11)$$
参数b的求解需要利用KKT条件，在前面式1.30求解参数$b$过程中利用的是支持向量，这里同样可以利用支持向量来求此参数$b$,在加入软间隔的条件下对于支持向量有${\zeta }_i=0$，并且所有求解出的${\alpha }_i$肯定不会全为0，根据KKT条件中的第二个等式有
$$1-{\zeta }_i-y_i(w^T{x}_i+b)=0(2.12)$$
令${\zeta }_i=0$代入式2.12
$$\begin{gathered} 1-y_i(w^T\ast x_i+b)=0 \\ =>b=y_i-w^T{x}_i=y_i-\sum _{j=1}^m{\alpha }_j{y}_j{K}_{ji}(2.13) \end{gathered}$$

2.2关于${\alpha }_i,{\zeta }_i$与支持向量间的关系

在加入软间隔之后，支持向量又如何表示，下面探讨下支持向量与${\alpha }_i,{\zeta }_i$之间的关系，我们将KKT条件重新描述
K K T 条件： ∂ ( w , b , ζ , α , μ i ) L = 0 ( 2.14 ) α i g ( x i ) = 0 ( 2.15 ) μ i ζ i = 0 ( 2.16 ) g ( x i ) ≤ 0 ( 2.17 ) α i ≥ 0 ( 2.18 ) μ i ≥ 0 ( 2.19 ) i ∈ { 1 , 2 , . . . m } KKT条件：\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\\partial_{(w,b,\zeta,\alpha,\mu_i)}L=0\quad(2.14)\\\alpha_ig(x_i)=0\quad(2.15)\\\mu_i\zeta_i=0\quad(2.16)\\g(x_i)\leq0\quad(2.17)\\\alpha_i\geq0\quad(2.18)\\\mu_i\geq0\quad(2.19)\\i\in\{1,2,...m\} KKT条件：∂(w,b,ζ,α,μi​)​L=0(2.14)αi​g(xi​)=0(2.15)μi​ζi​=0(2.16)g(xi​)≤0(2.17)αi​≥0(2.18)μi​≥0(2.19)i∈{1,2,...m}
1.若$\alpha =0$,根据式2.7中第三个等式知道${\mu }_i=C\ne 0$,根据式2.16知道${\zeta }_i=0$,再根据式2.17知道$ y_i(w^Tx_i+b)\geq1$,此时知道样本$(x_i，y_i)$在划分间隔外，或者在分隔边界上。

2.若$0<\alpha <C$,根据式2.7中第三个等式知道$0<{\mu }_i<C$,根据2.16知道${\zeta }_i=0$,再根据式2.17再根据式2.17知道$ y_i(w^Tx_i+b)\geq1$,同时对于式2.15，即$ y_i(w^Tx_i+b)=1$，即说明样本在分隔边界上

3.若$\alpha =C$,根据式2.7中第三个等式知道${\mu }_i=0$,根据式2.16知道${\zeta }_i\ge 0$，根据式2.15有$ y_i(w^Tx_i+b)=1-\zeta_i\leq1$,此时知道样本$(x_i,y_i)$在划分边界内或者在划分边界上

结合上面三种情况，可以推出
$$\begin{gathered} {\alpha }_i=0<=>y_i(w^T{x}_i+b)\ge 1 \\ 0<{\alpha }_i<C<=>y_i(w^T{x}_i+b)=1(2.20) \\ {\alpha }_i=C<=>y_i(w^T{x}_i+b)\le 1 \end{gathered}$$

参考视频：简博士8 支持向量机（31）：SMO算法中参数变量的选择.MP4_哔哩哔哩_bilibili

参考书籍：《机器学习实战》peter,《机器学习》周志华，《统计学习方法》李航

参考博客：(33条消息) 支持向量机（SVM）—— 详细推导及案例应用可视化_svm算法应用实例_不会三刀流的索隆的博客-CSDN博客

​ 【机器学习】支持向量机 SVM（非常详细） - 知乎 (zhihu.com)

​ 支持向量机原理详解(一): 间隔最大化，支持向量 - 知乎 (zhihu.com)

​ 支持向量机原理详解(二): 拉格朗日对偶函数，SVM的对偶问题 - 知乎 (zhihu.com)

​ 支持向量机原理详解(七): 序列最小最优化(SMO)算法(Part II) - 知乎 (zhihu.com)

​ 支持向量机原理详解(六): 序列最小最优化(SMO)算法(Part I) - 知乎 (zhihu.com)