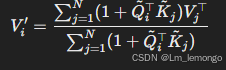一、摘要
Transformer 网络因全局感受野和adaptability to input逐渐取代 CNN，但 softmax-attention 的二次复杂度限制其在高分辨率图像去雾中的应用。为此，提出了一种名为 MB-TaylorFormer 的新型 Transformer 变体，通过泰勒展开近似 softmax-attention，实现线性复杂度，并结合多尺度注意力模块纠正误差。此外，引入多分支架构和多尺度补丁嵌入，以可变形卷积嵌入不同感受野和语义特征。在多个去雾基准上，MB-TaylorFormer 展现出领先性能和较低计算成本。
二、背景
图像去雾任务中的直接应用面临以下挑战：
1）Transformer 的计算复杂度随特征图分辨率呈二次增长，限制了其在像素级任务中的适用性；2）现有视觉 Transformer 通常通过固定卷积核生成固定尺度的特征标记，缺乏灵活性。为了解决这些问题，作者提出了基于泰勒展开的 Transformer 变体 TaylorFormer 和多分支结构 MB-TaylorFormer。
TaylorFormer 通过对 softmax 进行泰勒展开实现线性计算复杂度，同时保持全局建模能力，并在像素级交互中提供更精细的特征处理。为修正泰勒展开的误差，加入了多尺度注意力细化模块（MSAR），通过卷积提取局部信息，生成与多头自注意力对应的缩放因子，提高性能的同时计算开销极低。
针对特征标记的固定尺度问题，MB-TaylorFormer 采用多分支编码器-解码器架构，结合多尺度补丁嵌入模块，通过变形卷积生成具有多尺度、多维度特征的标记，并利用深度可分离方法减少计算复杂度。多分支结构可以同时处理不同尺度的特征标记，捕获更强大的特征。
实验结果表明，MB-TaylorFormer 在多种合成和真实去雾数据集上实现了参数量和计算量较低的同时，达到了最先进（SOTA）的性能。
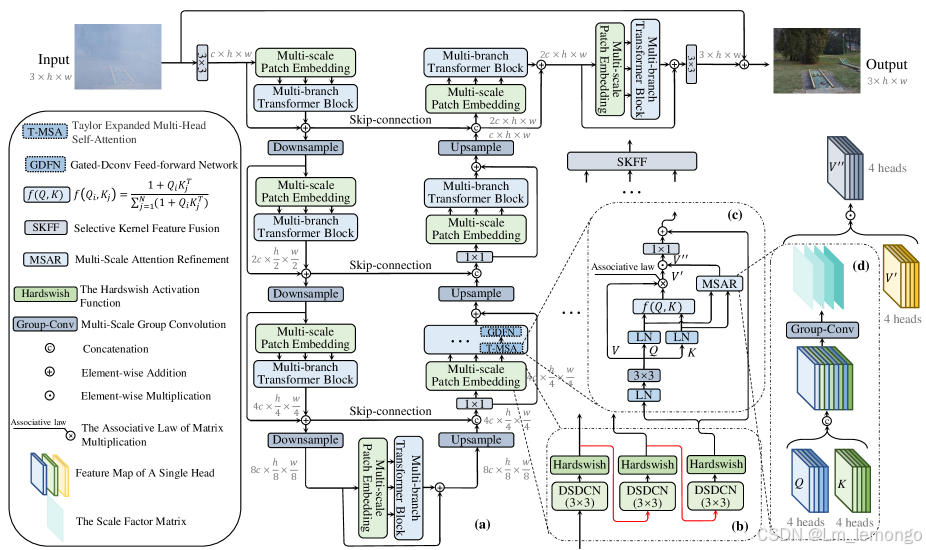
图 ：MB-TaylorFormer 的架构
(a) MB-TaylorFormer 采用了基于多尺度补丁嵌入的多分支分层设计。
(b) 多尺度补丁嵌入 实现从粗略到精细的特征嵌入。
(c) TaylorFormer 提供线性计算复杂度的注意力机制。
(d) MSAR 模块 用于补偿泰勒展开中的误差。
三、MB-TaylorFormer
MB-TaylorFormer 是一种高效轻量级的基于 Transformer 的去雾网络，旨在降低计算复杂度。通过对 Softmax-attention 的泰勒展开，满足结合律并结合类似 Restormer 的 U-net 结构。此外，为了弥补泰勒展开误差的影响，提出了 MSAR 模块。核心模块包括多尺度 patch 嵌入（Multi-scale Patch Embedding）、泰勒展开自注意力（Taylor Expanded Self-Attention）以及 MSAR 模块。
3.1 多分支主干网络
给定输入雾图 
- 初始通过卷积提取浅层特征，生成
。
- 每个阶段包含一个残差块，该块由多尺度 patch 嵌入和多分支 Transformer 块组成：
- 多尺度 patch 嵌入：生成多尺度的视觉 token。
- 多分支 Transformer 块：每个分支包含多个 Transformer 编码器。
- 使用 SKFF 模块融合分支生成的特征。
- 采样操作：采用像素重排列（pixel-unshuffle 和 pixel-shuffle）进行下采样和上采样。
- 跳跃连接：结合编码器和解码器的信息，除第一阶段外使用 1×1卷积降维。
- 在编码-解码后添加残差块，恢复结构和纹理细节。
- 最终用 3×3 卷积生成残差图
，并通过 I′=I+R 输出去雾后的图像。
为进一步压缩计算量，模型采用深度可分离卷积（Depthwise Separable Convolutions, DSDCN）。
3.2 多尺度 Patch 嵌入
针对固定卷积核的问题，提出了一种新的多尺度 patch 嵌入，具有以下特点：
- 多种感受野尺寸：使用不同尺度的可变形卷积核（DCN）并行生成粗细粒度的视觉 token。
- 多层语义信息：堆叠小核的可变形卷积层，提升深度和语义信息。
- 灵活的感受野形状：通过限制偏移范围（如 [−3,3]），实现对局部区域的关注。
通过引入 DSDCN（深度可分离与可变形卷积），显著降低了计算复杂度和参数量：
- DSDCN 的计算复杂度和参数量分别比标准 DCN 更低。
感受野范围的限制实验表明，合理地设置 token 的感受野可提升模型性能。
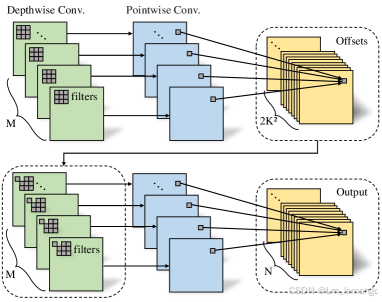
DSDCN 的结构说明
DSDCN 的流程可以分为两个主要部分：偏移生成和特征提取。
偏移生成：
- 首先，使用标准的 K×K深度卷积（Depthwise Convolution） 提取空间特征。
- 然后，通过 逐点卷积（Pointwise Convolution, 1×1 卷积） 生成每个位置的偏移量。
- 偏移量用于灵活调整卷积核的采样位置，以增强局部感受野的适应性。
特征提取：
- 利用 K×K 的 深度可变形卷积（Depthwise Deformable Convolution, DCN） 进行特征提取。DCN 使用偏移量调整卷积核的位置，从而适应不同的局部区域特性。
- 最后，通过一个逐点卷积整合深度卷积生成的特征，输出结果。
3.3 泰勒展开的多头自注意力（T-MSA）
传统的自注意力（MSA）计算复杂度为
核心方法：
-
将 Softmax 替换为泰勒公式的一阶展开：
其中，Q~i和 K~j是经过归一化的向量。
-
通过矩阵乘法的结合律进行优化，显著减少计算复杂度。
-
使用深度卷积生成 Q、K、V，强调局部上下文，并逐层增加多头结构的数量。
实验结果表明，在处理高分辨率图像时，T-MSA 能接近 MSA 的性能，同时大幅降低计算成本。
3.4 多尺度注意力优化
在多尺度注意力优化（MSAR）模块中，为了解决 T-MSA（Taylor-Multi-Scale Attention）中的近似误差，采用了局部信息学习来校正误差并提升高频信息处理能力。具体来说，通过将多头注意力机制中的 Q 和 K 矩阵重塑为 Qm,
其中
论文地址：2308.14036