前言

1. 猴群 (Monkey Algorithm,MA)算法。由 Ruiqing 和 Wansheng 等于 2008 年提出。
2. 主要模仿了猴群爬山过程的行为。

截止到 2023 年，算法引用趋势

1. 猴群相关的生物群行为

猴群爬山的行为模式

• 攀爬过程：猴子通过攀爬达到一个山顶
• 瞭望过程：如果爬到山顶则向四周瞭望以寻找更高的山峰
• 跳跃过程：找到了更高的山峰则跳跃过去继续攀登
• 空翻过程：为了发现更高的山峰猴子需要空翻到更远的地方

2. 算法仿生设计

2.1 概述

根据猴群的爬山行为表现，MA 的过程也分为三种过程：攀爬过程，望-跳过程和空翻过程。

1. 首先将猴群的位置进行初始化。
2. 攀爬：每只猴子都找到一个山顶。
3. 望-跳：猴子瞭望四周，寻找是否有比当前更高的点，有则跳过去。
4. 空翻：猴子望一个支点的方向进行空翻，以到达新的搜索区域。
5. 对上述每个步骤进行迭代，并且对整个过程进行迭代。

2.2 攀爬过程

1.猴子个体 $i$ 首先探查依据伪梯度方向从点 $X_i=(X_i,1,X_i,2,X_i,3,\dots ,X_i,d)$ 前进一步到达的位置 $P_i$

• 随机产生序列向量 $\Delta X_i:$
  $$\Delta X_i=(\Delta X_{i,1},\Delta X_{i,2},...,\Delta X_{i,Di})$$

• 计算伪梯度：
  $$f_{i,d}(X_{i,d})=\frac{(f(X_{i,d}+\Delta X_{i,d})-(f(X_{i,d}-\Delta X_{i,d})}{2\Delta X_{i,d}}$$

• 更新位置信息：
  $$P{{}^{\prime }}_{i,d}=X{{}^{\prime }}_{i,d}+a\ast sign(f_{i,d}(X_{i,d}))$$

2.若 $P_i$ 超出 $X$ 的取值范围：$[X_{l}d,X_{u}d]$，则 $P_i$ 取边界值。

3.计算该猴子个体在 $P_i$ 位置上的目标函数值 $F(P_i)$ 。若 $F(P_i)<F(X_i)$ ，则 $X_i$ 替换为 $P_i$ ，否则不变。

4.重复执行这些操作步骤，直到达到最大攀爬次数 $T_{max}$ 或者目标函数值没有什么变化。

2.3 望-跳过程

1. 猴子个体 $i$ 从当前所在位置点 $X_i=(X_i,1,X_i,2,X_i,3,\dots ,X_i,d)$ 向四周望去，视线的落脚点位置为 $P_i$ ，其中，$P_{i,d}$ 的值为：
   $$P_{i,d}=rand(0,1)\ast (X_{i,d}-\phi X_{i,d}+\phi )$$
   其中 $\phi$ 为视野宽度，即猴子从所在点出发向外能观望的最远的距离。
2. 若 $P_i$ 超出 $X$ 的取值范围：$[X_{ld},X_{ud}]$，则 $P_i$ 取边界值。
3. 若 $P_i\in [X_{ld},X_{ud}]$，计算目标函数值 $F(P_i)$ 。若 $F(P_i)<F(X_i)$ ，则猴子 跳至点 $P_i$ ，更新位置信息。
4. 否则不跳， 重复望跳行为

1. 猴子个体以空翻半径 $\mu$ 的长度进行空翻行为，其中 $\mu$ 在空翻区域 $[b,c]$ 内取任意值：
   $$\mu =rand(0,1)\ast [b,c]$$
2. 空翻的支点为群体的重心 $X=(X_1,X_2,\dots ,X_{Di})$ , 则 空 翻 后 得 到 的 位 置 点 为 $P_i$ ，其中
   $$P_{i,d}=X_{i,d}+\mu \ast (X_{i,d}–X_{i,d})$$
3. 若 $P_i$ 超出 $X$ 的取值范围：$[X_{ld},X_{ud}]$ ，则 $P_i$ 取边界值。
4. 若空翻落点 $P_i\in [X_{ld},X_{ud}]$ ，计算目标函数值 $F(P_i)$ 。
5. 若 $F(P_i)<F(X_i)$ ， 则空翻成功，更新位置信息。否则，不空翻，继续上述操作。

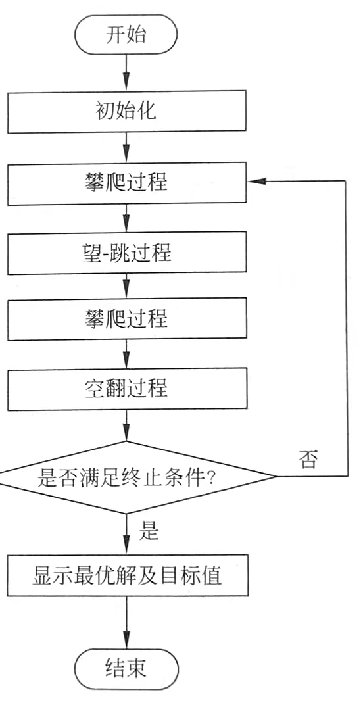
3. 算法流程

1. 猴群位置 $X_i$ 初始化。设置种群中个体总数 $SN$，变量数目 $D_i$，攀爬步长 $a$ ，视野宽度 $\phi$ ，空翻区域 $[b,c]$，最大攀爬次数 $T_{max}$ 以及最大迭代数 $K_{max}$ 。 位置点 $X_i=(X_{i,1},X_{i,2},X_{i,3},\dots ,X_{i,d})$ 的初始化公式为：
   $$X_{i,d}=rand(0,1)\ast (X_{u,d}-X_{i,d})+X_{i,d}$$
2. 第 $i$ 只猴子个体从当前位置出发，执行攀爬行为，更新位置信息。
3. 执行望跳行为，更新位置信息。
4. 执行空翻行为，更新位置信息。
5. 判断是否满足结束条件(到达求解精度)或者是否到达最大迭代次数 $K_{max}$ 。若满足，则终止算法。否则，返回 2。
6. 输出全局最优解及它相应的位置信息。

4. 算法特点

• MA 能够有效地求解高维的、非线性不可微的函数优化问题。
• 调控参数少，结构简单易操作，CPU消耗低等特点。
• 算法本身的“空翻”特点，使得它在算法收敛后期易跳出局部最优。
• 观跳行为和空翻行为存在很多的随机性，这中间的过程可能会耗费较多的时间
• 虽然猴群算法特有的空翻行为能帮助它很好地跳出局部最优值，但是空翻行为也存在极大的随机性，导致求解精度不佳。

5. 算法相关改进

• 解决离散变量组合问题时可能存在失效的问题，将猴群个体的位置信息运用整数编码方法，改进了算法的初始化方式

• 在攀爬行为中引进了“好动算法”，通过细微随机地调整猴子位置信息中的若干变量，进行精细的目标搜寻

• 对攀爬行为中依靠伪梯度计算前进的缺陷，重新定义攀爬行为

• 在算法后期观望行为中运用循环次数递增机制，提高了算法的求解效率

• 在猴群算法的攀爬、 观跳行为中引入混沌特征

• 将病毒算法和猴群算法相融合

• 将病毒算法和鱼群算法较强的局部寻优能力结合

• 对于算法本身的思想、原理、参数设置以及种群多样性的研究，仍停留在实验探索阶段，并未有更深入的分析与讨论。关于算法收敛性的分析与证明的研究还未出现。对猴群算法的改进技术主要集中于增加参数、与其它算法混合等方面，对于算法框架、迭代进化方式等的改进的研究较少。

Reference

Zhao, Ruiqing & Tang, Wansheng. (2008). Monkey algorithm for global numerical optimization. Journal of Uncertain Systems. 2. 165-176.