文章目录
1.插入排序(Insertion Sort)
1.1 简介
插入排序(Insertion Sort)是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,找到合适位置并插入。
插入排序(Insertion Sort)是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,找到合适位置并插入。
1.2 插入排序的步骤
- 初始状态:假设第一个元素已经排序(即长度为1的数组是有序的)。
- 遍历未排序部分:从第二个元素开始,依次取出每一个元素。
- 插入元素:
- 将已取出的元素(记为key)与已排序部分的元素从后向前比较。
- 如果已排序部分的元素大于key,则将该元素向后移动一位。
- 重复上述步骤,直到找到key的合适位置,将其插入。
- 重复:重复步骤2和3,直到所有元素均已排序。
1.3 插入排序的C实现
#include <stdio.h>
// 插入排序函数
void insertionSort(int arr[], int n) {
int i, key, j;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
// 将arr[i]插入到已排序的arr[0..i-1]部分
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
// 打印数组函数
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// 主函数
int main() {
int arr[] = {12, 11, 13, 5, 6};
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序前的数组: \n");
printArray(arr, n);
insertionSort(arr, n);
printf("排序后的数组: \n");
printArray(arr, n);
return 0;
}
1.4 插入排序的时间复杂度
- 最佳情况:O(n)(数组已经是有序的)
- 最坏情况:O(n2)(数组是逆序的)
- 平均情况:O(n2)
1.5 插入排序的空间复杂度
- 插入排序是in-place排序算法,因此其空间复杂度为O(1)。
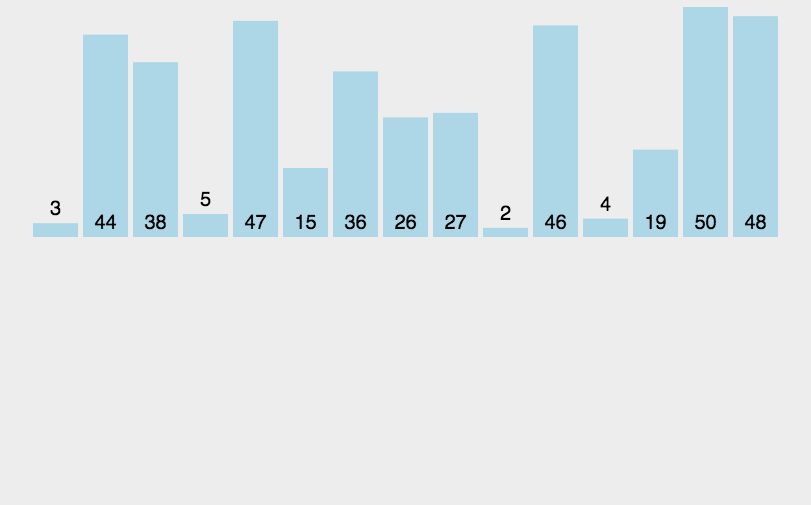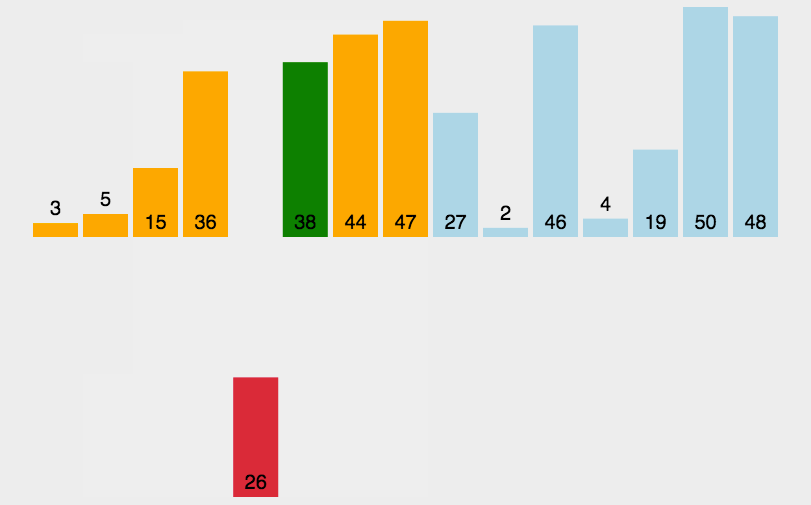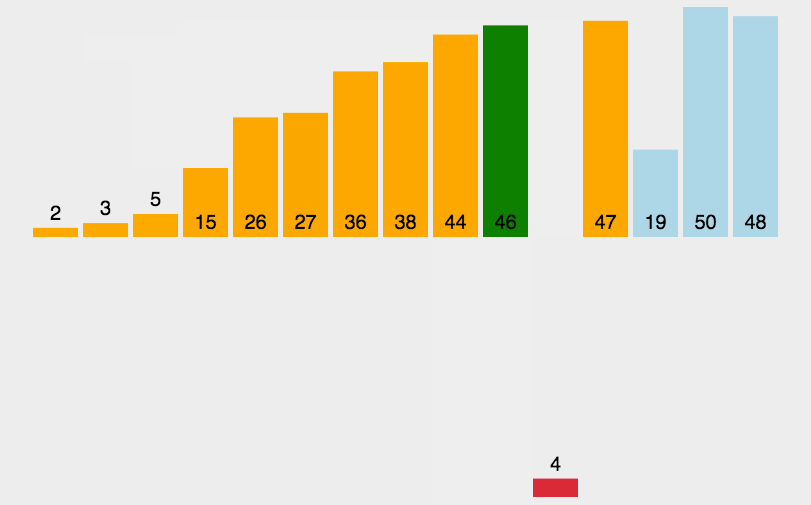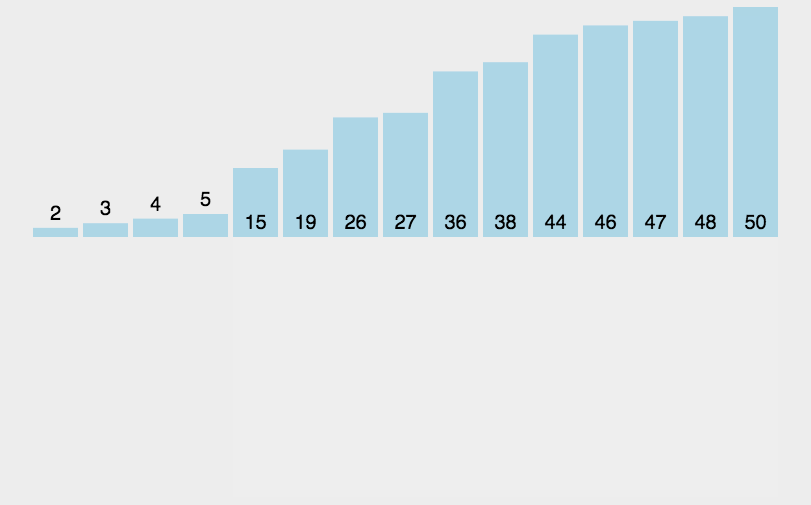
1.6 插入排序的动画
2. 二分插入排序(Binary Insertion Sort)
2.1 简介
它通过引入二分查找(Binary Search)算法来优化查找插入位置的过程。在标准的插入排序中,为了将当前元素插入到已排序部分的正确位置,算法需要从后向前扫描已排序部分,直到找到比当前元素大的第一个元素或到达数组的开头。
2.2 二分插入排序步骤
- 从数组的第二个元素开始,将每个元素视为待插入元素。
- 使用二分查找算法在已排序部分中查找待插入元素的正确位置。
- 将已排序部分中大于待插入元素的元素向后移动一位,以腾出空间。
- 将待插入元素插入到正确位置。
- 重复步骤1-4,直到数组完全排序。
2.3 二分插入排序C语言实现
#include <stdio.h>
// 二分查找函数,返回插入位置的前一个索引
int binarySearch(int arr[], int item, int low, int high) {
if (high <= low)
return (item > arr[low]) ? (low + 1) : low;
int mid = (low + high) / 2;
if (item == arr[mid])
return mid + 1;
if (item > arr[mid])
return binarySearch(arr, item, mid + 1, high);
return binarySearch(arr, item, low, mid - 1);
}
// 二分插入排序函数
void binaryInsertionSort(int arr[], int n) {
int i, j, key, loc;
for (i = 1; i < n; i++) {
key = arr[i];
// 使用二分查找找到插入位置
loc = binarySearch(arr, key, 0, i - 1);
// 移动元素以腾出空间
for (j = i - 1; j >= loc; j--) {
arr[j + 1] = arr[j];
}
arr[loc] = key;
}
}
// 打印数组函数
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
// 主函数
int main() {
int arr[] = {37, 23, 0, 17, 12, 72, 31, 46, 100, 88, 54};
int n = sizeof(arr) / sizeof(arr[0]);
printf("排序前的数组: \n");
printArray(arr, n);
binaryInsertionSort(arr, n);
printf("排序后的数组: \n");
printArray(arr, n);
return 0;
}
二分插入排序的时间和空间复杂度分析如下:
2.4 二分插入排序的时间复杂度
二分插入排序的时间复杂度主要由两部分组成:二分查找和元素移动。
- 二分查找:在每次插入时,使用二分查找来确定插入位置。二分查找的时间复杂度是对数级别的,即O(log n),其中n是已排序部分的长度。然而,需要注意的是,这里的n并不是整个数组的长度,而是已排序部分的长度。在插入排序的过程中,已排序部分的长度是逐渐增加的。
- 元素移动:当找到插入位置后,需要将该位置及其之后的元素向后移动一位,以腾出空间插入新元素。这个过程的时间复杂度是线性的,即O(n),其中n是已排序部分的长度(在插入当前元素之前的长度)。在最坏情况下,当前元素可能需要被插入到已排序部分的开头,导致所有已排序的元素都需要向后移动一位。
由于二分插入排序在每次插入时都需要进行二分查找和元素移动,因此其总体时间复杂度仍然是O(n2)。这是因为,虽然二分查找减少了比较次数,但元素移动的次数并没有减少。在插入n个元素的过程中,每个元素都可能需要进行O(n)次的移动(在最坏情况下),因此总的时间复杂度是O(n2)。
2.5 二分插入排序的时间复杂度
二分插入排序是就地排序算法(in-place sorting algorithm),它不需要额外的存储空间来存储中间结果。算法在排序过程中只需要几个额外的变量来存储临时值和索引,因此其空间复杂度是O(1)。
综上所述,二分插入排序的时间复杂度是O(n2),空间复杂度是O(1)。这些复杂度特性使得二分插入排序在处理小规模数据集或几乎已排序的数据集时可能表现出较好的性能,但在处理大规模数据集时则不是最优选择。