基本介绍&快速入门&张量Tensor&数据集Dataset&数据变换Transforms&网络构建&函数式自动微分&模型训练&保存与加载

模型训练

模型训练一般分为四个步骤：

1. 构建数据集。
2. 定义神经网络模型。
3. 定义超参、损失函数及优化器。
4. 输入数据集进行训练与评估。

构建数据集

首先从数据集 Dataset加载代码，构建数据集。

import mindspore
from mindspore import nn
from mindspore.dataset import vision, transforms
from mindspore.dataset import MnistDataset

# 下载数据
from download import download

url = "https://mindspore-website.obs.cn-north-4.myhuaweicloud.com/" \
      "notebook/datasets/MNIST_Data.zip"
path = download(url, "./", kind="zip", replace=True)


def datapipe(path, batch_size):
    image_transforms = [
        vision.Rescale(1.0 / 255.0, 0),
        vision.Normalize(mean=(0.1307,), std=(0.3081,)),
        vision.HWC2CHW()
    ]
    label_transform = transforms.TypeCast(mindspore.int32)

    dataset = MnistDataset(path)
    dataset = dataset.map(image_transforms, 'image')
    dataset = dataset.map(label_transform, 'label')
    dataset = dataset.batch(batch_size)
    return dataset

train_dataset = datapipe('MNIST_Data/train', batch_size=64)
test_dataset = datapipe('MNIST_Data/test', batch_size=64)

输出：

file_sizes: 100%|███████████████████████████| 10.8M/10.8M [00:00<00:00, 150MB/s]
Extracting zip file...
Successfully downloaded / unzipped to ./

定义神经网络模型

从网络构建中加载代码，构建一个神经网络模型。

class Network(nn.Cell):
    def __init__(self):
        super().__init__()
        self.flatten = nn.Flatten()
        self.dense_relu_sequential = nn.SequentialCell(
            nn.Dense(28*28, 512),
            nn.ReLU(),
            nn.Dense(512, 512),
            nn.ReLU(),
            nn.Dense(512, 10)
        )

    def construct(self, x):
        x = self.flatten(x)
        logits = self.dense_relu_sequential(x)
        return logits

model = Network()

定义超参、损失函数和优化器

超参

超参（Hyperparameters）是可以调整的参数，可以控制模型训练优化的过程，不同的超参数值可能会影响模型训练和收敛速度。目前深度学习模型多采用批量随机梯度下降算法进行优化，随机梯度下降算法的原理如下：

$$w_{t+1}=w_t-\eta \frac{1}{n}\sum _{x\in \mathcal{B}}\nabla l\left(x,w_t\right)$$

公式中，$n$是批量大小（batch size），$\eta$是学习率（learning rate）。另外，$w_t$为训练轮次$t$中的权重参数，$\nabla l$为损失函数的导数。除了梯度本身，这两个因子直接决定了模型的权重更新，从优化本身来看，它们是影响模型性能收敛最重要的参数。一般会定义以下超参用于训练：

• 训练轮次（epoch）：训练时遍历数据集的次数。

• 批次大小（batch size）：数据集进行分批读取训练，设定每个批次数据的大小。batch size过小，花费时间多，同时梯度震荡严重，不利于收敛；batch size过大，不同batch的梯度方向没有任何变化，容易陷入局部极小值，因此需要选择合适的batch size，可以有效提高模型精度、全局收敛。

• 学习率（learning rate）：如果学习率偏小，会导致收敛的速度变慢，如果学习率偏大，则可能会导致训练不收敛等不可预测的结果。梯度下降法被广泛应用在最小化模型误差的参数优化算法上。梯度下降法通过多次迭代，并在每一步中最小化损失函数来预估模型的参数。学习率就是在迭代过程中，会控制模型的学习进度。

epochs = 3
batch_size = 64
learning_rate = 1e-2

损失函数

损失函数（loss function）用于评估模型的预测值（logits）和目标值（targets）之间的误差。训练模型时，随机初始化的神经网络模型开始时会预测出错误的结果。损失函数会评估预测结果与目标值的相异程度，模型训练的目标即为降低损失函数求得的误差。

常见的损失函数包括用于回归任务的nn.MSELoss（均方误差）和用于分类的nn.NLLLoss（负对数似然）等。 nn.CrossEntropyLoss 结合了nn.LogSoftmax和nn.NLLLoss，可以对logits 进行归一化并计算预测误差。

在数学上，MSE定义为：
$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$

• $n$为记录数
• $i$是从1开始的记录索引
• $y_i$表示实际值
• $\widehat{y_i}$是记录的预测值

二元交叉熵损失：
$$-\frac{1}{N}\sum _{i=1}^N(y_i\cdot log(p_i)+(1-y_i)log(1-p_i))$$

• $y_i$true标签
• $p_i$模型预测的概率

多类交叉熵损失：
$$-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^C(y_{i,j}\cdot log(p_{i,j}))$$

loss_fn = nn.CrossEntropyLoss()

• $C$是类别的数量
• $y_{i,j}$是$j$类实例$i$的真是标签
• $p_{i,j}$是针对实例$i$的类别$j$的预测概率

优化器

模型优化（Optimization）是在每个训练步骤中调整模型参数以减少模型误差的过程。MindSpore提供多种优化算法的实现，称之为优化器（Optimizer）。优化器内部定义了模型的参数优化过程（即梯度如何更新至模型参数），所有优化逻辑都封装在优化器对象中。在这里，我们使用SGD（Stochastic Gradient Descent）优化器。

我们通过model.trainable_params()方法获得模型的可训练参数，并传入学习率超参来初始化优化器。

optimizer = nn.SGD(model.trainable_params(), learning_rate=learning_rate)

在训练过程中，通过微分函数可计算获得参数对应的梯度，将其传入优化器中即可实现参数优化，具体形态如下：

grads = grad_fn(inputs)
optimizer(grads)

训练与评估

设置了超参、损失函数和优化器后，我们就可以循环输入数据来训练模型。一次数据集的完整迭代循环称为一轮（epoch）。每轮执行训练时包括两个步骤：

1. 训练：迭代训练数据集，并尝试收敛到最佳参数。
2. 验证/测试：迭代测试数据集，以检查模型性能是否提升。

接下来我们定义用于训练的train_loop函数和用于测试的test_loop函数。

使用函数式自动微分，需先定义正向函数forward_fn，使用value_and_grad获得微分函数grad_fn。然后，我们将微分函数和优化器的执行封装为train_step函数，接下来循环迭代数据集进行训练即可。

# 定义前向传播
def forward_fn(data, label):
    logits = model(data)
    loss = loss_fn(logits, label)
    return loss, logits

# 梯度函数
grad_fn = mindspore.value_and_grad(forward_fn, None, optimizer.parameters, has_aux=True)

# 定义一步训练函数
def train_step(data, label):
    (loss, _), grads = grad_fn(data, label)
    optimizer(grads)
    return loss

def train_loop(model, dataset):
    size = dataset.get_dataset_size()
    model.set_train()
    for batch, (data, label) in enumerate(dataset.create_tuple_iterator()):
        loss = train_step(data, label)

        if batch % 100 == 0:
            loss, current = loss.asnumpy(), batch
            print(f"loss: {loss:>7f}  [{current:>3d}/{size:>3d}]")

test_loop函数同样需循环遍历数据集，调用模型计算loss和Accuray并返回最终结果。

def test_loop(model, dataset, loss_fn):
    num_batches = dataset.get_dataset_size()
    model.set_train(False)
    total, test_loss, correct = 0, 0, 0
    for data, label in dataset.create_tuple_iterator():
        pred = model(data)
        total += len(data)
        test_loss += loss_fn(pred, label).asnumpy()
        correct += (pred.argmax(1) == label).asnumpy().sum()
    test_loss /= num_batches
    correct /= total
    print(f"Test: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")

我们将实例化的损失函数和优化器传入train_loop和test_loop中。训练3轮并输出loss和Accuracy，查看性能变化。

loss_fn = nn.CrossEntropyLoss()
optimizer = nn.SGD(model.trainable_params(), learning_rate=learning_rate)

for t in range(epochs):
    print(f"Epoch {t+1}\n-------------------------------")
    train_loop(model, train_dataset)
    test_loop(model, test_dataset, loss_fn)
print("Done!")

输出：

Epoch 1
-------------------------------
loss: 2.316752  [  0/938]
loss: 1.718842  [100/938]
loss: 0.854982  [200/938]
loss: 0.664822  [300/938]
loss: 0.522135  [400/938]
loss: 0.594073  [500/938]
loss: 0.536049  [600/938]
loss: 0.300968  [700/938]
loss: 0.295295  [800/938]
loss: 0.264794  [900/938]
Test: 
 Accuracy: 91.1%, Avg loss: 0.311748 

Epoch 2
-------------------------------
loss: 0.556006  [  0/938]
loss: 0.326711  [100/938]
loss: 0.242640  [200/938]
loss: 0.230652  [300/938]
loss: 0.347568  [400/938]
loss: 0.107691  [500/938]
loss: 0.463003  [600/938]
loss: 0.234526  [700/938]
loss: 0.211332  [800/938]
loss: 0.260454  [900/938]
Test: 
 Accuracy: 93.1%, Avg loss: 0.244732 

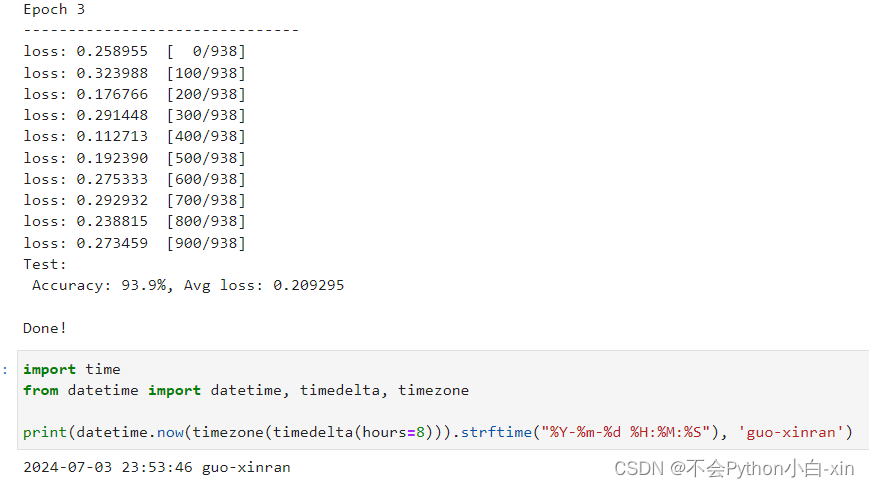
Epoch 3
-------------------------------
loss: 0.258955  [  0/938]
loss: 0.323988  [100/938]
loss: 0.176766  [200/938]
loss: 0.291448  [300/938]
loss: 0.112713  [400/938]
loss: 0.192390  [500/938]
loss: 0.275333  [600/938]
loss: 0.292932  [700/938]
loss: 0.238815  [800/938]
loss: 0.273459  [900/938]
Test: 
 Accuracy: 93.9%, Avg loss: 0.209295 

Done!