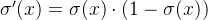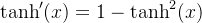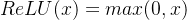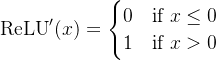1. Sigmoid函数

• 范围：输出值在0到1之间。
• 导数：
• 优点：简单直观，适用于二分类问题的输出层。
• 缺点：在输入值较大或较小时，梯度会变得非常小（梯度消失），这会导致深层网络训练困难。同时，Sigmoid函数的输出不是以0为中心的，这可能会导致梯度下降过程中的不稳定。

应用场景：常用于二分类问题的输出层，早期的全连接层中也会使用。

2.  Tanh（双曲正切函数）

• 范围：输出值在-1到1之间。
• 导数：
• 优点：相比Sigmoid，tanh函数的输出以0为中心，这有助于梯度的传播。对于输入值较小或较大的情况，梯度的消失问题相对较轻。
• 缺点：当输入值非常大或非常小时，tanh函数的梯度仍然会接近于零（梯度消失）。

应用场景：适用于中间层的激活函数，尤其是在需要负值和正值的情况中。

3.  ReLU()激活函数

• 范围：输出值在0到正无穷之间。
• 导数：
• 优点：计算简单，梯度计算效率高，减少了梯度消失的问题，有助于加速网络的收敛。
• 缺点：可能导致“死亡神经元”问题，即大量神经元输出恒为0，无法进行有效的训练。

应用场景：广泛应用于隐藏层的激活函数，是现代深度学习模型中的默认选择。