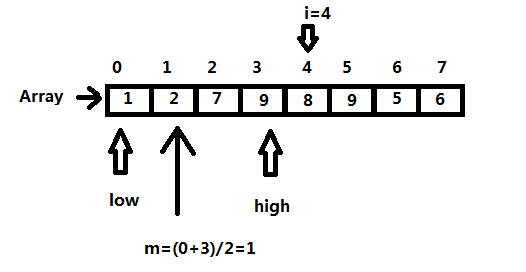
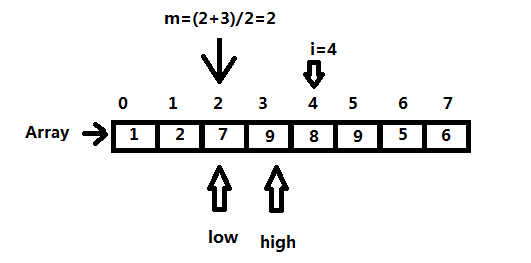
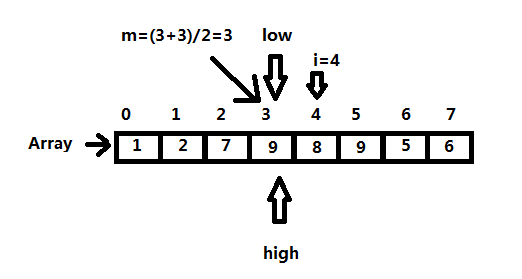
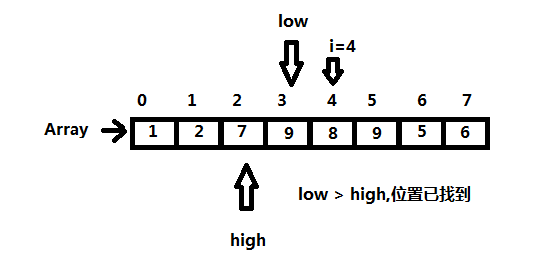
二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

是稳定的排序方法

时间复杂度:O(n^2)

 二、查找过程
首先计算表中间的位置，将表中间位置处的关键字与查找的关键字进行比较，如果相等，则查找成功；否则利用中间位置将表分为前、后两个子表，如果中间位置的关键字大于查找的关键字，则查找前子表，否则查找后子表。重复上面的过程，直到找到要查找的关键字为止，否则查找失败不存在此关键字。
 

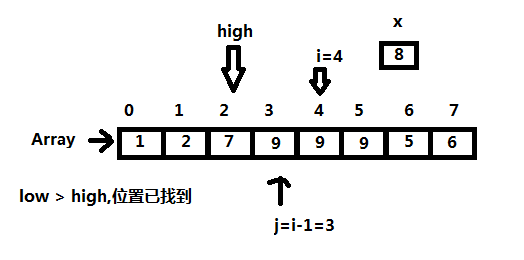
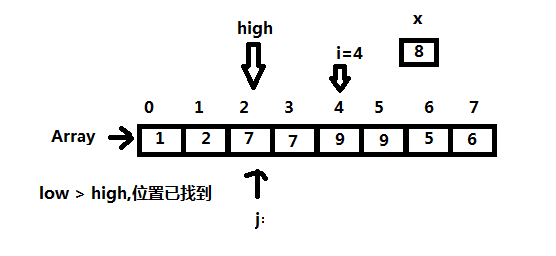
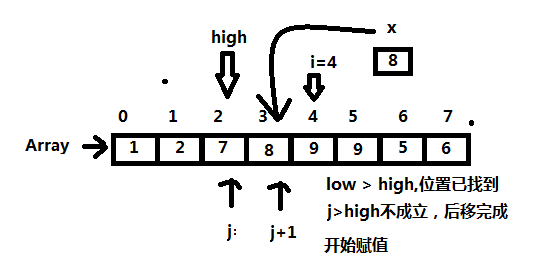
图示：以i=4时为例：

阅读者可仔细思考一下里面的逻辑，理清思路

第一步

第二步

第三步：

第四步：

第五步：

第六步：

第七步：

public class InsertSort {

    public static void main(String[] arg) {
        int[] a=new int[] {49,38,65,97,76,13,27};
        int n=a.length;
        InsertSort1(a,n);
    }


     static void InsertSort1(int a[],int n) {
        int i,j,low,high,mid,temp;
        int h=1;
        for (i=1;i<n;i++){
            //将a[i]暂存到中间变量，从第二个数开始与前面的数开始依次比较并排序
            temp=a[i];
            low=0;high=i-1;
            //判断low是否小于high,如果小于则执行while循环
            while(low<=high){
                mid=(low+high)/2;
                //取中间索引位置与temp比较,不断寻找它要插入的位置，知道不满足low<high退出循环
                if (a[mid]>temp) high=mid-1;
                else low=mid+1;
            }
            //位置寻找完毕，开始进行数据插入，然后进行到下一个最外层的for循环
            for (j=i-1;j>=high+1;--j){
                a[j+1]=a[j];
            }
            a[high+1]=temp;

            //遍历打印每一次插入排序的结果
            for(int c=0;c<n;c++) {
                System.out.print(a[c]+" ");
            }

            //第几次排序
            System.out.println("第"+ h++ +"次排序");
        }
   }
}


38 49 65 97 76 13 27 第1次排序
38 49 65 97 76 13 27 第2次排序
38 49 65 97 76 13 27 第3次排序
38 49 65 76 97 13 27 第4次排序
13 38 49 65 76 97 27 第5次排序
13 27 38 49 65 76 97 第6次排序