一、题目：

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

二、解答：

1. 暴力破解但是算法的时间复杂度为O(m+n)。

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) 
    {
        int m = nums1.size();
        int n = nums2.size();
        vector<int>::iterator it1 = nums2.begin();
        //合并两个数组
        while(it1 != nums2.end())
        {
            //nums1.resize(m+n);
            nums1.push_back(*it1);
            it1++;
        }
        //对合并完成的数组进行排序
        sort(nums1.begin(),nums1.end());
        //偶数情况
        if((m+n)%2 == 0)
        {
            vector<int>::iterator pose1 = nums1.begin();
            int count = (m+n) / 2 - 1;
            pose1 += count;
            double avg = (*pose1 + *(pose1 + 1)) / 2.0;
            return (avg > 0.0) ? avg : 0.00000;
        }
        //奇数情况
        else
        {
            vector<int>::iterator pose2 = nums1.begin();
            int count = (m+n-1)/2;
            pose2 += count;
            return (double)*pose2;
        }
    }
};

2.利用二分法来缩减时间复杂度。

解题思路：

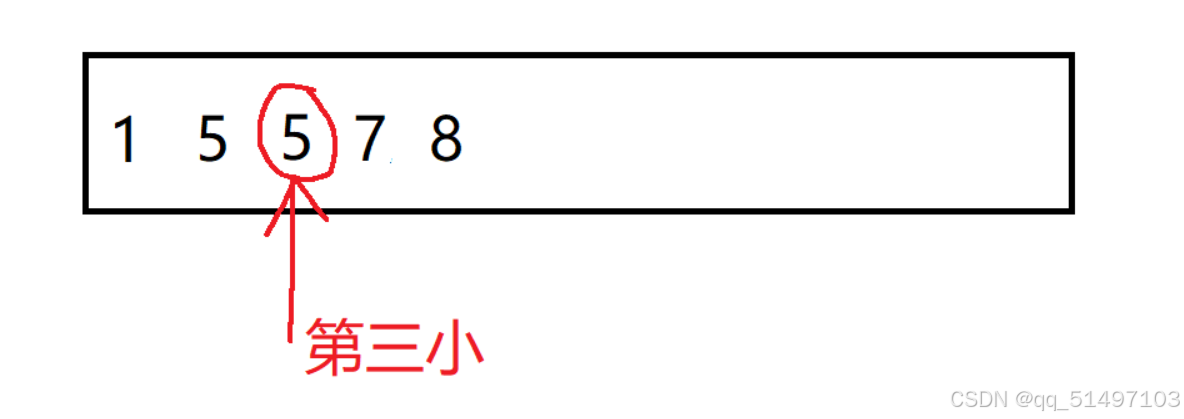
首先这是两个正序数组，我们想要找到中位数也就等价于找到第k小的数。

那么两个数组也是一样的思想，想要找到两个数组合并后的中位数也就等价于找到第k小的数。

假设两个数组的长度分别为m和n，那么中位数也就是第（m+n+1）/2小的数。当两个数组的长度之和为奇数时，我们只需要找到一个第k小的，它的值就是中位数的值。二当两个数组的长度之和为偶数时，那我们就需要找到第k小的数和第k+1小的数，把他们的和除以二就是中位数的值。这个算法的核心思路就是getkth函数，采用递归的思想去不断排除元素从而逼近中位数，递归的终止条件为找到第1小的数。

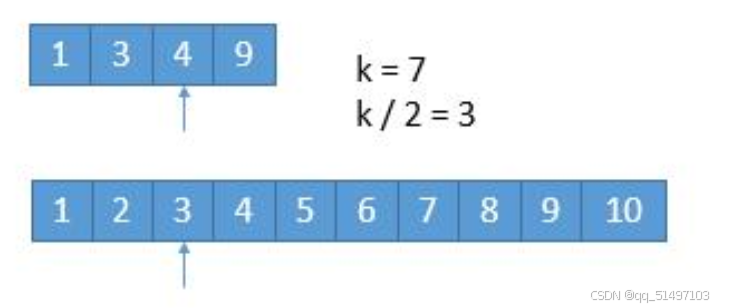
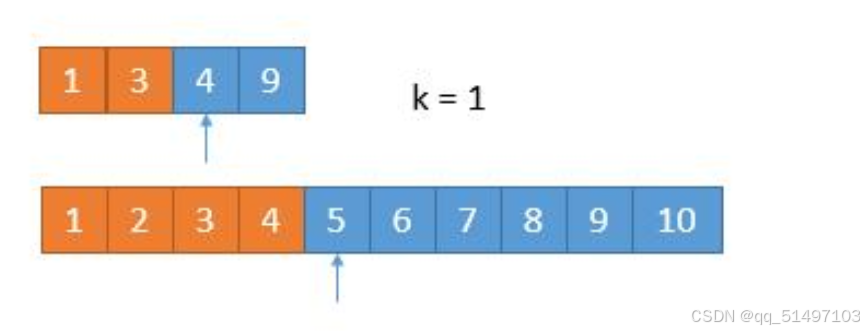
假设第一个数组为1、3、4、9

第二个数组为1、2、3、4、5、6、7、8、9、10

那么根据k = （m+n+1）/2 = 7

所以我们要找第7小的数。每次都取两个数组的前k/2个，也就是前三个。通过对比两个数组的前三个我们发现4是大于3的，也就是说第二个数组的3是不可能成为第7小的，那么由于数组时正序的，第二个数组的前三个元素就可以删除，从而减少了k/2个元素。

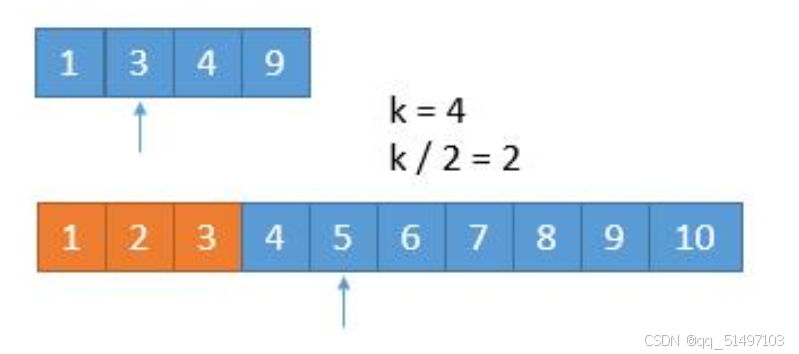
去除了第二个数组的前三个元素后任务也会发生改变，从原来的寻找第7小变成了（7-3=4）第4小的数，那么这一步需要对比的数位4/2 = 2。将两个数组的前两个数中最大的数进行对比，发现5是大于3的，那么第一个数组的前两个数不可能是第4小的数，就可以将第一个数组的前两个数删除。

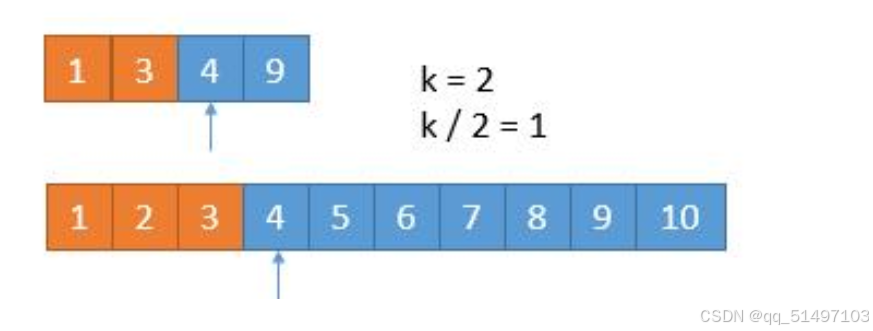
去除了第一个数组的前两个元素后任务也会发生改变，从原来的寻找第4小变成了（4-2=2）第2小的数，那么这一步需要对比的数位2/2 =1。但此时出现了两个都是4，我们假设第一个的4大于第二个的4，将第二个数组的4删除。

最终我们需要找到第一小的数，也就是来到了递归的判定点，我们只需要取出两个数组的第一个元素进行比对，谁小那么他就是我们要寻找的中位数。

代码：

class Solution {
public:
    double findMedianSortedArrays(std::vector<int>& nums1, std::vector<int>& nums2) {
        int n = nums1.size();
        int m = nums2.size();
        //当n+m为偶数时，left=right
        //当n+m为奇数时，left+1=right
        int left = (n + m + 1) / 2;
        int right = (n + m + 2) / 2;
        
        return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
    }
    
    int getKth(std::vector<int>& nums1, int start1, int end1, std::vector<int>& nums2, int start2, int end2, int k) {
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;
        //当第一个数组的长度大于第二个数组的长度，将两个数组进行交换为了后续的运算
        if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);
        //当第一个数组为空时，只需要返回第二个数组中第start2 + k - 1小的数
        if (len1 == 0) return nums2[start2 + k - 1];
        //递归的终止条件
        if (k == 1) return std::min(nums1[start1], nums2[start2]);
        
        int i = start1 + std::min(len1, k / 2) - 1;
        int j = start2 + std::min(len2, k / 2) - 1;
        
        if (nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));
        } else {
            return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));
        }
    }
};