目录
150栈操作,239队列操作,347大顶堆小顶堆
150. 逆波兰表达式求值
逆波兰表达式:是一种后缀表达式,所谓后缀就是指运算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
-
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
-
适合用栈操作运算:遇到数字则入栈;遇到运算符则取出栈顶两个数字进行计算,并将结果压入栈
逆波兰表达式相当于是二叉树中的后序遍历。
(中缀表达式对于计算机来说就不是很友好,因为计算机判断出运算符后不能直接运算,还要比较优先级,后缀表达式不需要考虑优先级了,直接利用栈来顺序处理。)
Integer.valueOf(s) 功能:将一个字符串解析为一个 Integer 对象。
class Solution {
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList<>();
for (String s : tokens) {
if ("+".equals(s)) { // leetcode 内置jdk的问题,不能使用==判断字符串是否相等
stack.push(stack.pop() + stack.pop());
} else if ("-".equals(s)) { // 注意 - 和/ 需要特殊处理
stack.push(-stack.pop() + stack.pop());
} else if ("*".equals(s)) {
stack.push(stack.pop() * stack.pop());
} else if ("/".equals(s)) {
int temp1 = stack.pop();
int temp2 = stack.pop();
stack.push(temp2 / temp1);
} else {
stack.push(Integer.valueOf(s));
}
}
return stack.pop();
}
}239. 滑动窗口最大值(有点难)
感觉自己独立很难code出来,虽然思路是理解了。
这是使用单调队列的经典题目。需要一个队列,将元素放进窗口,随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值即可。
需要我们自己来实现一个单调队列。单调队列,即单调递减或单调递增的队列。因为队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。
例如 {2, 3, 5, 1 ,4} ,单调队列里只维护 {5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
- pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
- push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
方法1:自定义数组
重点理解在add(),主要作用是向双端队列中添加元素,同时确保队列中的元素按降序排列。每次添加新元素时,移除所有小于新元素的末尾元素,从而保持队列的顺序。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
//方法1:自定义数组
if (nums.length == 1) {
return nums;
}
int len = nums.length - k + 1;
//存放结果元素的数组
int[] res = new int[len];
int num = 0;
//自定义队列
MyQueue myQueue = new MyQueue();
//先将前k的元素放入队列
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
//滑动窗口移除最前面的元素,移除是判断该元素是否放入队列
myQueue.poll(nums[i - k]);
//滑动窗口加入最后面的元素
myQueue.add(nums[i]);
//记录对应的最大值
res[num++] = myQueue.peek();
}
return res;
}
}
class MyQueue {
Deque<Integer> deque = new LinkedList<>();
//弹出元素时,比较当前要弹出的数值是否等于队列出口的数值,如果相等则弹出
//同时判断队列当前是否为空
void poll(int val) {
if (!deque.isEmpty() && val == deque.peek()) {
deque.poll();
}
}
//添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出
//保证队列元素单调递减
//比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
void add(int val) {
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
deque.add(val);
}
//队列队顶元素始终为最大值
int peek() {
return deque.peek();
}
}方法2:双端队列实现
理解一下。
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
//方法2:利用双端队列手动实现单调队列
/**
* 用一个单调队列来存储对应的下标,每当窗口滑动的时候,直接取队列的头部指针对应的值放入结果集即可
* 单调队列类似 (tail -->) 3 --> 2 --> 1 --> 0 (--> head) (右边为头结点,元素存的是下标)
*/
ArrayDeque<Integer> deque = new ArrayDeque<>();
int n = nums.length;
int[] res = new int[n - k + 1];
int idx = 0;
for (int i = 0; i < n; i++) {
// 根据题意,i为nums下标,是要在[i - k + 1, i] 中选到最大值,只需要保证两点
// 1.队列头结点需要在[i - k + 1, i]范围内,不符合则要弹出
while (!deque.isEmpty() && deque.peek() < i - k + 1) {
deque.poll();
}
// 2.既然是单调,就要保证每次放进去的数字要比末尾的都大,否则也弹出
while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
deque.offer(i);
// 因为单调,当i增长到符合第一个k范围的时候,每滑动一步都将队列头节点放入结果就行了
if (i >= k - 1) {
res[idx++] = nums[deque.peek()];
}
}
return res;
}
}347.前 K 个高频元素
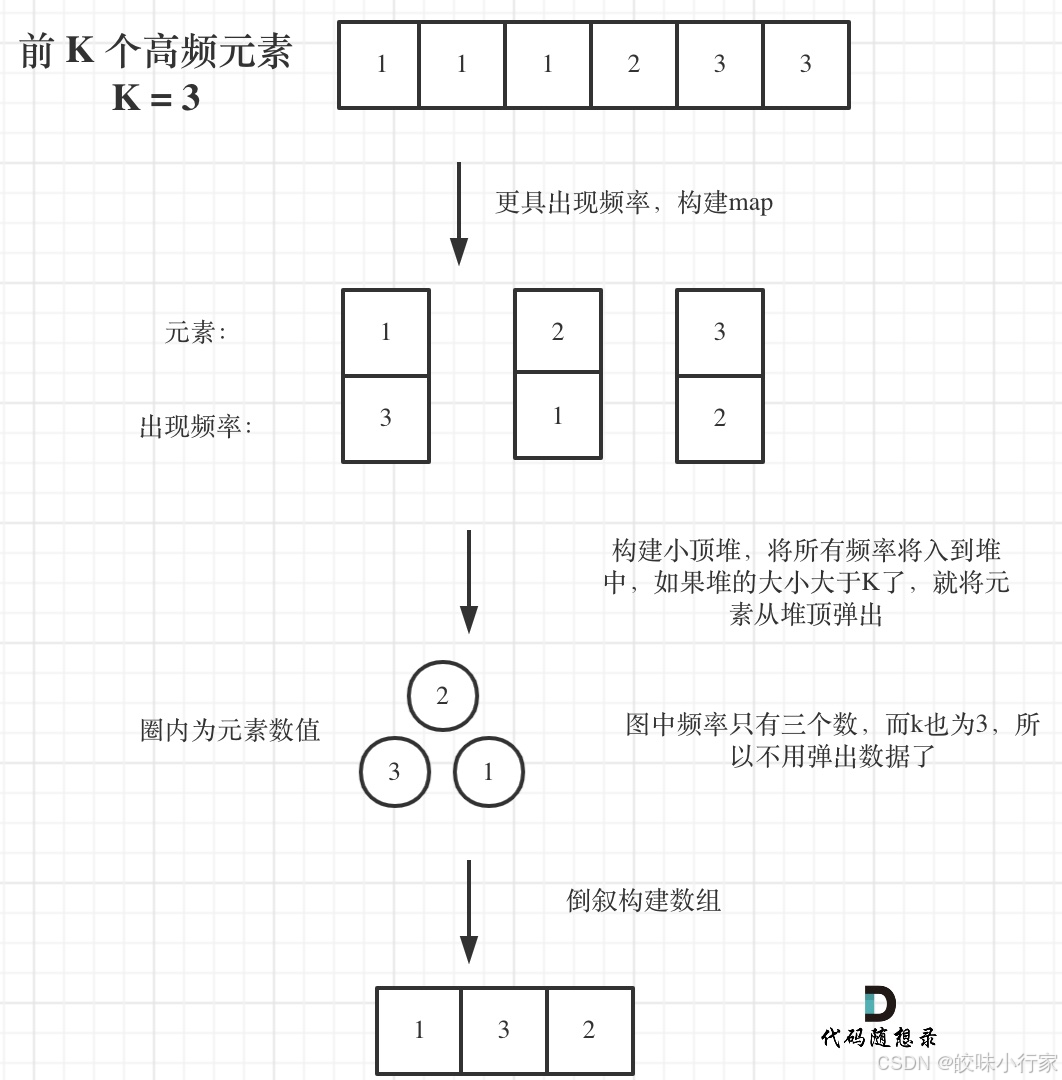
思路主要涉及到如下三块内容:
- 统计元素出现频率(使用map(key,value))
- 对频率排序(优先级队列-->小顶堆)
- 找出前K个高频元素
优先级队列:
其实就是一个披着队列外衣的堆,因为优先级队列对外接口只是从队头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列。缺省情况下priority_queue利用max-heap(大顶堆)完成对元素的排序,这个大顶堆是以vector为表现形式的complete binary tree(完全二叉树)。
堆是一棵完全二叉树,大顶堆(堆头是最大元素),小顶堆(堆头是最小元素)。优先级队列从小到大排就是小顶堆,从大到小排就是大顶堆。
(为什么不用快排呢, 使用快排要将map转换为vector的结构,然后对整个数组进行排序, 而这种场景下,我们其实只需要维护k个有序的序列就可以了,所以使用优先级队列是最优的。)
· 是使用小顶堆呢,还是大顶堆?
要用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。(pop的是堆顶的元素)
总体流程如图所示:
Code注释详解:
在Java中,PriorityQueue 是一个基于堆的数据结构,它的排序是在元素插入和删除时自动进行的。
实现小顶堆:PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair2[1] - pair1[1]);
这段代码创建了一个 PriorityQueue,其元素为 int[] 数组,并使用自定义的比较器来决定队列中元素的顺序。具体来说,队列中元素按每个数组的第二个元素(索引为1)进行升序排序。
pair1[1] - pair2[1] 的结果决定了 PriorityQueue 的排序规则。如果结果为负数,表示 pair1 的第二个元素小于 pair2 的第二个元素,pair1 应排在 pair2 之前。
实现大顶堆:PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair2[1] - pair1[1]);
这段代码创建了一个 PriorityQueue,其元素为 int[] 数组,并使用自定义的比较器来决定队列中元素的顺序。具体来说,队列中元素按每个数组的第二个元素(索引为1)进行降序排序。
PriorityQueue 是 Java 中的一个类,实现了优先队列的数据结构。优先队列是一种基于堆的数据结构,支持在对元素进行排序的基础上进行快速插入和删除操作。
(pair1, pair2) -> pair2[1] - pair1[1] 是一个自定义的比较器,使用 lambda 表达式来定义。pair2[1] - pair1[1] 的结果决定了 PriorityQueue 的排序规则:如果结果为负数,表示 pair2 的第二个元素小于 pair1 的第二个元素,pair2 应排在 pair1 之后。
遍历 Map 集合:for(Map.Entry<Integer, Integer> entry : map.entrySet())
Map.Entry是Map接口的一个内部接口,用于表示Map中的一个键值对(entry)。map.entrySet()方法返回一个Set集合,这个集合包含了map中的所有键值对(Map.Entry对象)。entry.getKey()获取当前键值对的键,entry.getValue()获取当前键值对的值。
var 关键字:for (var x : map.entrySet())
var 关键字:这里的 var 关键字使得编译器自动推断变量 x 的类型。在这个例子中,var entry 的类型会被推断为 Map.Entry<Integer, Integer>。
var是 Java 10 引入的一个关键字,用于局部变量类型推断。它可以根据变量的初始值来自动推断变量的类型。var只能用于局部变量声明,不能用于字段、方法参数、返回类型等。
在Java中,PriorityQueue 是一个基于堆的数据结构,它的排序是在元素插入和删除时自动进行的。
计算频次:
map.put(num, map.getOrDefault(num, 0) + 1);
方法1:基于大顶堆实现
大顶堆需要对所有元素进行排序,将所有数据加入大顶堆中,最终取出前k个元素,即就是出现频率前k高的元素。
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 方法1:基于大顶堆实现
Map<Integer, Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
//在优先队列中存储二元组(num, cnt),cnt表示元素值num在数组中的出现次数
//出现次数按从队头到队尾的顺序是从大到小排,出现次数最多的在队头(相当于大顶堆)
PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair2[1] - pair1[1]);
for (Map.Entry<Integer, Integer> entry : map.entrySet()) { //大顶堆需要对所有元素进行排序
pq.add(new int[]{entry.getKey(), entry.getValue()});
}
int[] ans = new int[k];
for (int i = 0; i < k; i++) { //依次从队头弹出k个,就是出现频率前k高的元素
ans[i] = pq.poll()[0];
}
return ans;
}
}方法2:基于小顶堆实现
不再需要在队列中添加所有元素,而是只需要维护k个元素。元素大于k的时候做比较,弹出堆头即最小元素。最终做了一个倒序输出,因为队列中是从小到大排列的。
创建数组的方法:
- 静态初始化
int[] arr = {1, 2, 3, 4, 5};
- 动态初始化
int[] arr = new int[5]; // 创建一个包含5个元素的数组
arr[0] = 1;
arr[1] = 2;
- 创建并立即初始化
int[] arr = new int[]{1, 2, 3, 4, 5};
String[] strArr = new String[]{"Hello", "World"};
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 方法2:基于小顶堆实现
Map<Integer, Integer> map = new HashMap<>();//key为数组元素值,val为对应出现次数
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
//在优先队列中存储二元组(num, cnt),cnt表示元素值num在数组中的出现次数
//出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair1[1] - pair2[1]);
for (Map.Entry<Integer, Integer> entry : map.entrySet()) { //小顶堆只需要维持k个元素有序
if (pq.size() < k) { //小顶堆元素个数小于k个时直接加
pq.add(new int[]{entry.getKey(), entry.getValue()});
} else {
if (entry.getValue() > pq.peek()[1]) { //当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
pq.poll(); //弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
pq.add(new int[]{entry.getKey(), entry.getValue()});
}
}
}
int[] ans = new int[k];
// 倒叙弹出
for (int i = k - 1; i >= 0; i--) { //依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
ans[i] = pq.poll()[0];
}
return ans;
}
}方法3:基于小顶堆的简化实现
最后倒不倒序都可以,因为本题目中不限制输出顺序,若需要求,则可考虑。
class Solution {
public int[] topKFrequent(int[] nums, int k) {
// 方法3:基于小顶堆的简化实现
// 优先级队列,为了避免复杂 api 操作,pq 存储数组
// lambda 表达式设置优先级队列从大到小存储 o1 - o2 为从小到大,o2 - o1 反之
PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
int[] res = new int[k]; // 答案数组为 k 个元素
Map<Integer, Integer> map = new HashMap<>(); // 记录元素出现次数
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
for (var x : map.entrySet()) { // entrySet 获取 k-v Set 集合
// 将 kv 转化成数组
int[] tmp = new int[2];
tmp[0] = x.getKey();
tmp[1] = x.getValue();
pq.offer(tmp);
// 下面的代码是根据小根堆实现的,我只保留优先队列的最后的k个,只要超出了k我就将最小的弹出,剩余的k个就是答案
if (pq.size()>k){
pq.poll();
}
}
for (int i = 0; i <k; i++) {
res[i] = pq.poll()[0];
}
return res;
}
}第十一天的总算是结束了,直冲Day13!(12是休息Day✌)