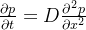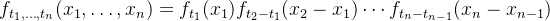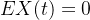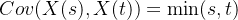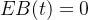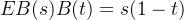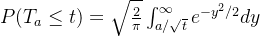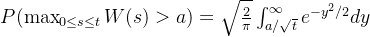随机过程基础：4.Brown(布朗)运动

一、定义

Brown运动，也称为Wiener过程，是由英国植物学家Robert Brown在1827年发现的。他观察到悬浮在液体中的小颗粒粒子进行非常不规则的运动。这种运动是因为颗粒受到液体中分子的不断碰撞。这种运动后来被称为Brown运动。Brown运动的数学解释由爱因斯坦在1905年提出，并在1918年由维纳精确地数学公式化。

数学定义：设X(t) 表示一个粒子在Brown运动中的 x 方向分量， x0为粒子在时刻 t0 的位置，即 X(t0)=x0。设 p(x;t∣x0) 表示在给定X(t0)=x0 的条件下 X(t+t0) 的条件概率密度。我们假设所给的转移概率是平稳的，从而 p(x;t∣x0) 不依赖于起始时刻t0。

扩散方程：爱因斯坦证明了p(x;t∣x0) 必然满足偏微分方程：

$\frac{\partial p}{\partial t} = D \frac{\partial^2 p}{\partial x^2}$

p：表示在某个位置和某个时间，颗粒出现的概率密度。
t：表示时间。
x：表示位置。
D：是扩散系数，它表示颗粒扩散的速度。
这个方程的意思是：某个位置的颗粒浓度（概率密度）随时间的变化，取决于颗粒在该位置周围的分布情况。具体来说，位置变化的二阶导数（表示位置上的变化率）乘以一个扩散系数D，决定了颗粒浓度随时间的变化率。

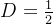
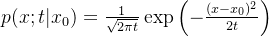
选择适当的单位，我们可以取 $D = \frac{1}{2}$ ，于是我们可以直接验证 $p(x; t|x_0) = \frac{1}{\sqrt{2\pi t}} \exp \left( -\frac{(x - x_0)^2}{2t} \right)$ 是上述扩散方程的解。

随机游动逼近：考虑对称随机游动，每次移动Δx，其中Xn表示粒子在第n时刻运动的方向， Sn=(X1+⋯+Xn)Δx 表示在时刻n 粒子的位置。通过适当的极限过程，可以让单位转移时间趋于0，同时让步长适当收缩到0，从而由随机游动逼近Brown运动。

就像你手里有一枚硬币。每次你抛硬币，如果是正面，你就向前走一小步；如果是反面，你就向后走一小步。

每次移动Δx：这就像是你每次抛硬币后，决定走的那一小步的距离。
Xn表示粒子在第n时刻运动的方向：这就像是每次抛硬币的结果，决定了你是向前还是向后。
Sn=(X1+⋯+Xn)Δx：这就像是你在玩了n次抛硬币游戏后，你总共走了多少步。如果正面多，你就向前走了多步；如果反面多，你就向后走了多步。
单位转移时间趋于0：这就像是每次抛硬币的时间间隔变得非常非常短。
步长适当收缩到0：这就像是每次走的步子变得非常非常小。这样，你的运动就会变得非常复杂，就像是在做Brown运动。

随机过程{X(t); t>0} 称为Brown运动，如果它满足如下三个条件：

X(0) = 0
随机过程 X 有平稳独立增量
对每个 t > 0，X(t) 服从均值为0，方差为t 的正态分布

二、性质

1.连续性：Brown运动的几乎每条样本轨道是连续的，但几乎点点都没有导数。

2.Markov性质：Brown运动是一个齐次Markov过程，即在给定现在状态 X(s) 的条件下，过去 X(v);0≤v<s 与将来 X(t+s);t>0 独立。也就是上一篇介绍的马尔科夫的性质：你到达一个岔路口（这就是“现在状态 X(s)”），你要向左走还是向右走。这个决定只基于你当前的位置，而不依赖于你之前是如何到达这个岔路口的（这就是“过去 X(v); 0 ≤ v < s”），也不关心你将来会到达哪里（这就是“将来 X(t+s); t > 0”）。

3.联合分布：Brown运动的联合分布密度函数满足：

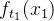
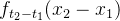
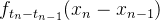
$f_{t_1, \ldots, t_n}(x_1, \ldots, x_n) = f_{t_1}(x_1)f_{t_2-t_1}(x_2 - x_1) \cdots f_{t_n-t_{n-1}}(x_n - x_{n-1})$

$f_{t_1}(x_1)$ ：这是粒子在时间t1时在位置x1的几率。

$f_{t_2-t_1}(x_2 - x_1)$ ：这是粒子在时间t2时，相对于时间t1的位置变化的几率。即：在t1时粒子在x1，经过(t2 - t1)的时间后，粒子移动到x2。

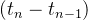
$f_{t_n-t_{n-1}}(x_n - x_{n-1})$ ：这是粒子在时间tn时，相对于时间 $t_{n-1}$ 的位置变化的几率。即：在 $t_{n-1}$ 时粒子在 $x_{n-1}$ ，经过 $(t_n - t_{n-1})$ 的时间后，粒子移动到 x_n 。

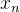
而粒子在不同时间点的移动是一个接一个的独立事件，每个事件只取决于前一个位置和时间差。联合分布函数就是把这些独立事件的概率乘起来，得到粒子在一系列时间点上同时出现在一系列位置上的总几率。

4.Gauss过程：Brown运动是一个Gauss过程，Gauss过程是一种随机过程，其中任意有限个时间点的随机变量的联合分布是正态分布。对于Brown运动，它是一个Gauss过程，这意味着在任何时间点上，粒子的位置是一个正态分布的随机变量。其均值函数和协方差函数分别为：

EX(t) = 0

$Cov(X(s), X(t)) = \min(s, t)$

即在任何时间点 t，粒子的位置的期望值是0。在两个不同时间点 s 和 t 上，粒子位置的协方差是这两个时间点中较小的那个。

5.Brown桥：定义 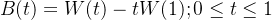$B(t) = W(t) - tW(1); 0 \leq t \leq 1$ 则 B 称为Brown桥过程。Brown桥过程也是Gauss过程，其均值函数和协方差函数分别为：

EB(t) = 0

EB(s)B(t) = s(1 - t)

想象你在公园里散步，你的小狗在你前面自由地跑来跑去。我们设定一个规则：小狗必须在散步的开始和结束时回到你的身边。小狗的运动可以看作是一个布朗桥过程。

开始时：小狗在你的身边，位置为0。
结束时：小狗再次回到你的身边，位置为0。
W(t)：小狗在时间 t 时的位置。
tW(1)：想象小狗在时间 1 时的位置的 t 倍。这相当于小狗在时间 1 时的位置被拉伸或压缩到时间t 的比例。
开始时（ t = 0 ）：
- W(0) = 0（因为布朗运动在时间0时的位置是0）。
- 0W(1) = 0（任何数乘以0都是0）。
- 所以，B(0) = W(0) - 0W(1) = 0 - 0 = 0。
结束时（ t = 1 ）：
- W(1) 是布朗运动在时间1时的位置。
- 1W(1) = W(1)（任何数乘以1都是它本身）。
- 所以，B(1) = W(1) - 1W(1) = W(1) - W(1) = 0。
B(t)：所以，小狗在时间 t 时的位置减去这个拉伸或压缩后的位置，确保了小狗在开始和结束时都在你的身边，即位置为0。

6.首达时：首达时Ta是Brown运动首次到达a的时刻。其分布为：

$P(T_a \leq t) = \sqrt{\frac{2}{\pi}} \int_{a/\sqrt{t}}^{\infty} e^{-y^2/2} dy$

7.最大值：Brown运动在 [0, t] 上的最大值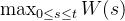 $\max_{0 \leq s \leq t} W(s)$ 的分布为：

$P(\max_{0 \leq s \leq t} W(s) > a) = \sqrt{\frac{2}{\pi}} \int_{a/\sqrt{t}}^{\infty} e^{-y^2/2} dy$

这两个表达式都是通过变量变换和积分推导出来的，涉及到标准正态分布的积分。首达时关注的是粒子首次到达某个位置的时间，而最大值关注的是粒子在某个时间区间内达到的最大位置。这些表达式在随机过程和概率论中非常重要，用于描述和预测粒子在随机运动中的行为。