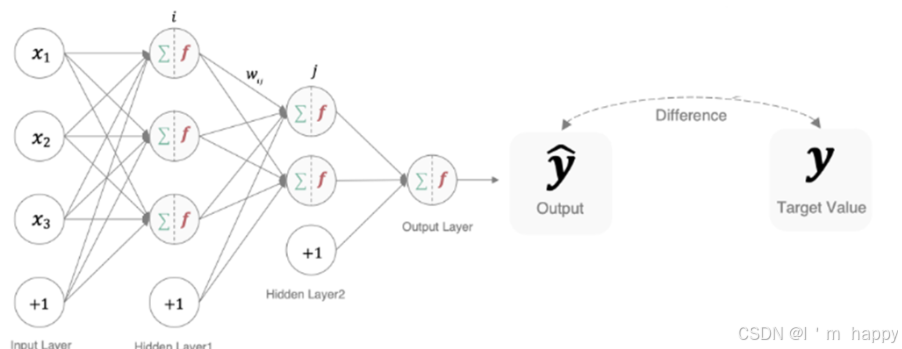
神经网络基础
1.损失函数
1.损失函数的概念
什么是损失函数
在深度学习中,**损失函数是用来衡量模型参数质量的函数,**衡量方式是比较网络输出和真实输出之间的差异.
不同文献中有不同命名方式
loss function:损失函数
cost function:代价函数
objective function:目标函数
error function:误差函数
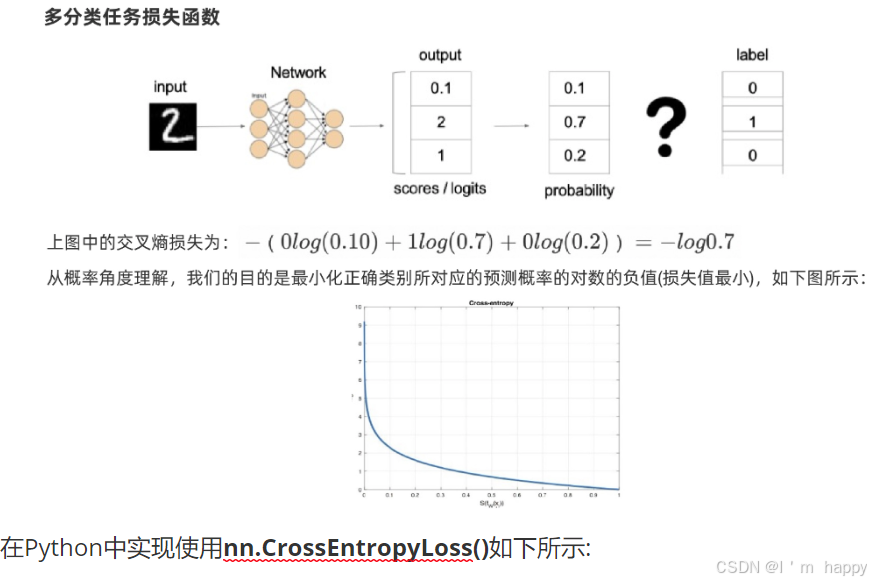
2.分类任务损失函数-多分类损失:
使用nn.CrossEntropyLoss()计算交叉熵损失值
多分类任务中通常使用softmax将logits(逻辑值)转换为概率形式,多分类的交叉熵损失也叫softmax 损失,计算方法是
L
=
−
∑
i
=
1
n
y
i
l
o
g
(
f
θ
(
X
i
)
)
L = -\sum_{i=1}^n{y_i}{log(f_θ(X_i))}
L=−i=1∑nyilog(fθ(Xi))
y是样本x属于某一个类别的真实概率
而f(x)是样本属于某一个类别的预测分数
s为softmax激活函数,将属于莫一类别的预测分数转换成概率
L是用来衡量真实值y与预测值f(x)之间差异性的损失结果
计算 L交叉熵的值越小越与真实值更加接近
在Python中实现使用nn.CrossEntropyLoss()如下所示:
# 构建多分类损失函数-CrossEntropy
import torch
from torch import nn
# 多分类任务交叉熵损失:使用nn.CrossEntropyLoss()实现
def test01():
# 设置真实值:可以是热编码后的结果也可以不是
y_true = torch.tensor([[0, 1, 0], [0, 0, 1]], dtype=torch.float32)
# 注意的类别必须是64为整数型
# y_true = torch.tensor([1, 2], dtype=torch.int64)
# 构建预测值计算损失结果
y_pred = torch.tensor([[0.2, 0.6, 0.2], [0.1, 0.8, 0.1]], dtype=torch.float32)
# 实例化交叉熵损失
loss = nn.CrossEntropyLoss()
# 计算损失结果:默认情况下,CrossEntropyLoss()会自动将预测值进行one-hot编码。
# 转换为numpy类型
my_loss = loss(y_pred, y_true).numpy()
print('loss', my_loss)
3.分类任务损失函数-二分类损失:
使用nn.BCELoss()计算二分类交叉熵
在处理二分类任务时使用sigmoid激活函数,使用二分类的交叉熵损失函数:
L = − y l o g y ^ − ( 1 − y ) l g ( 1 − y ^ ) L = -ylog\hat y - (1-y)lg(1-\hat y) L=−ylogy^−(1−y)lg(1−y^)
- y样本x属于某一个类别的真实概率
- 而y^是样本属于某一类别的预测概率
- L是衡量真实值与预测值之间差异性的损失结果
在Python实现nn.BCELoss()结果:如下所示
# 2-二分类-BCELoss.py
import torch
from torch import nn
def test01():
# 1.设置真实值与预测值
# 预测值为sigmoid()函数的输出结果
# requires_grad=True:表示需要计算梯度,用于反向传播。
y_pred = torch.tensor([0.6901, 0.5459, 0.2469], requires_grad=True)
y_true = torch.tensor([0, 1, 0], dtype=torch.float32)
# 2.实例化二分类交叉熵
loss = nn.BCELoss()
# 3,计算损失值
# 在 PyTorch 中,如果一个张量需要梯度(即 requires_grad=True),
# 则不能直接调用 .numpy() 方法,因为这会导致梯度信息丢失,从而影响反向传播
# 需要使用 .detach() 方法
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss', my_loss)
4.回归任务损失函数计算-MAE损失
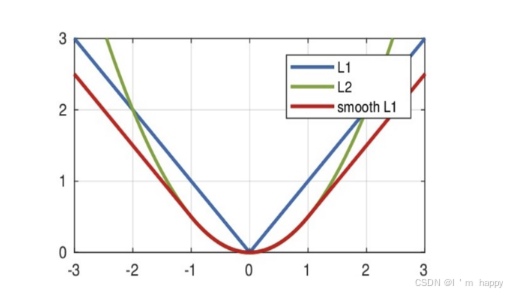
Mean absolute loss (MAE)被称为L1 Loss,以绝对误差作为距离,损失函数公式
L
=
1
n
∑
i
=
1
n
∣
y
i
−
f
θ
(
x
i
)
∣
L = \frac{1}{n}\sum_{i=1}^n|y_i-f_θ(x_i)|
L=n1i=1∑n∣yi−fθ(xi)∣
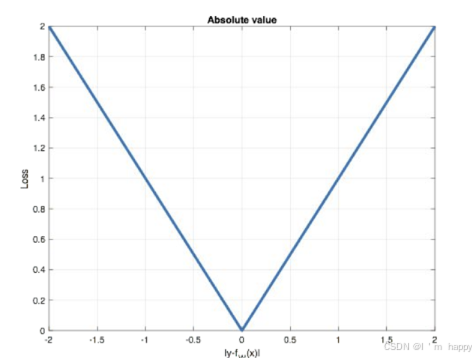
曲线图如下:
特点是
-
1.由于 LI Loss具有稀疏性,为了惩罚较大的值常作为正则化添加到其他loss中作为约束
-
2. L1 Loss最大问题就是零点梯度不平滑,导致会跳过极小值
在python中实现使用nn.L1Loss()实现
import torch
from torch import nn
def test01():
# 1.设置真实值与预测值
# requires_grad=True:表示需要计算梯度,前向传播会记录梯度,用于反向传播。
y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
y_true = torch.tensor([2.0, 2.0, 2.9], dtype=torch.float32)
# 2.实例化MAE损失对象
loss = nn.L1Loss()
# 3.计算损失
my_loss = loss(y_pred,y_true).detach().numpy()
print('loss',my_loss)
if __name__ == '__main__':
test01()
5.回归任务损失函数-MSE损失
MSE:L2 Loss 损失或者叫欧式距离,以误差的平方和的均值作为距离
损失公式
L
=
1
n
∑
i
=
1
n
(
y
i
−
f
θ
(
x
i
)
)
2
L = \frac{1}{n}\sum_{i=1}^n(y_i-fθ(x_i))^2
L=n1i=1∑n(yi−fθ(xi))2
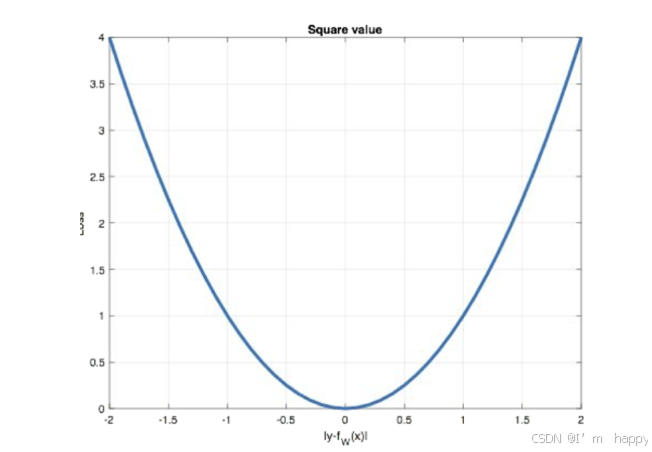
曲线图如下:
特点是:
1.L2 loss也常作为正则化项
2.当预测值与目标值相差较大时,梯度容易发生爆炸
在 python中使用nn.MSELoss()实现,如下所示
import torch
from torch import nn
def test01():
# 1.设置真实值与预测值
y_pred = torch.tensor([1.0, 1.0, 1.9], requires_grad=True)
y_true = torch.tensor([2.0, 2.0, 2.0], dtype=torch.float32)
# 2.实例化MSE损失对象
loss = nn.MSELoss()
# 3.计算损失
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss', my_loss)
if __name__ == '__main__':
test01()
6.回归任务损失函数-Smooth L1损失
smooth L1说的是光滑之后的L1,损失函数公式:
s
m
o
o
t
h
L
1
(
x
)
=
{
0.5
(
x
)
2
if
∣
x
∣
<
1
∣
x
∣
−
0.5
otherwise
smooth_{L1}(x) = \begin{cases} 0.5(x )^2 & \text{if } |x | < 1 \\ |x | - 0.5 & \text{otherwise} \end{cases}
smoothL1(x)={0.5(x)2∣x∣−0.5if ∣x∣<1otherwise
x = f(x) - y 为真实值 和 预测值之间的差值
从下图可以看出该函数实际为一个分段函数
1.在区间[-1,1]实际是L2损失,解决了L1不光滑问题
2.在区间[-1,1]外,实际就是L1损失,这就解决离群点爆炸问题
在python中使用 nn.SmoothL1Loss()实现,如下所示
import torch
from torch import nn
def test01():
# 1.设置真实值与预测值
y_pred = torch.tensor([0.6, 0.4], requires_grad=True)
y_true = torch.tensor([0, 3])
# 2.实例化SmoothL1损失对象
loss = nn.SmoothL1Loss()
# 3.计算损失
# detach():将损失张量从计算图中分离出来,不影响梯度计算
my_loss = loss(y_pred, y_true).detach().numpy()
print('loss', my_loss)
if __name__ == '__main__':
test01()
2.网络优化方法
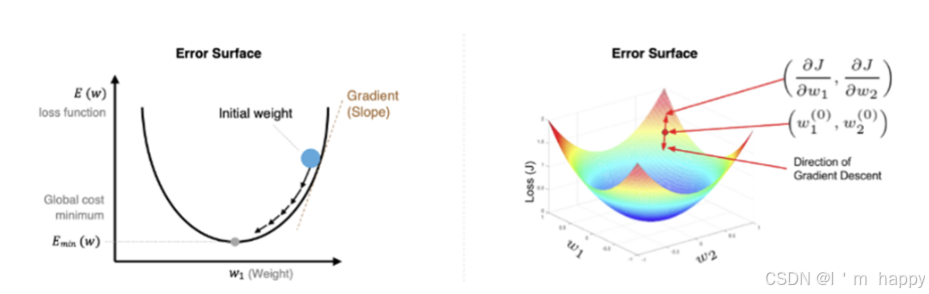
1.梯度下降算法
梯度下降法是一种寻找使损失函数最小化的方法,从数学的角度看,梯度方向是函数增长最快的方向, 梯度的反方向就是函数减少最快的方向,所以有:
W
i
j
n
e
w
=
W
i
j
o
i
d
−
α
∂
E
∂
W
i
j
W_{ij}^{new} = W_{ij}^{oid} - α\frac{∂E}{∂W_{ij}}
Wijnew=Wijoid−α∂Wij∂E
其中α为学习率,如果学习率太小,得到的效果就太小,增大训练成本.学习率太大可能跳过最优解,解决方法是,让学习率需要需要随着训练的进行而变化.
在进行模型训练时,有三个基础概念:
-
Epoch:使用全部数据对模型进行完整的训练,训练轮次
-
Batch_size:使用 训练集中小部分样本对模型权重进行以此反向传播的参数的更新,每次训练每批次的数据
-
Iteration:使用一个Batch的数据对模型进行一次参数的更新的过程
# 假设数据集有 50000 个训练样本,现在选择 Batch Size = 256 对模型进行训练。
- 每个 Epoch 要训练的图片数量:50000
- 训练集具有的 Batch 个数:50000/256+1=196
- 每个 Epoch 具有的 Iteration 个数:196
- 10个 Epoch 具有的 Iteration 个数:1960
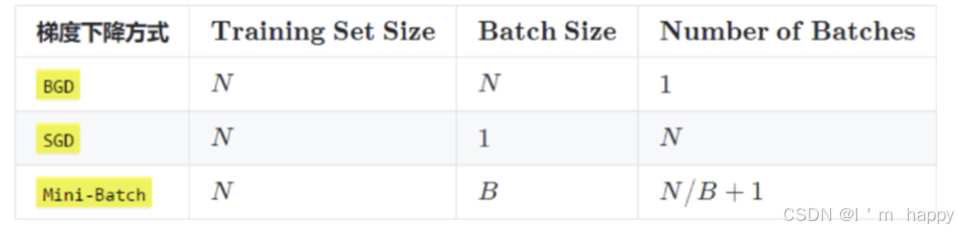
在深度学习过程中,梯度下降的几种方式根本区别在于Batch_size的不同,如下表所示:
注:上表中Mini-Batch的Batch个数为N/B+1是针对未整除的情况,整除则是N/B
2.反向传播算法(BP算法)
**前向传播:**指的是数据输入的神经网络中,逐层向前传输,一直=运输到输出层为止
**反向传播:利用损失函数从后往前,结合梯度下降算法,**依次对各个参数的偏导,并进行参数更新
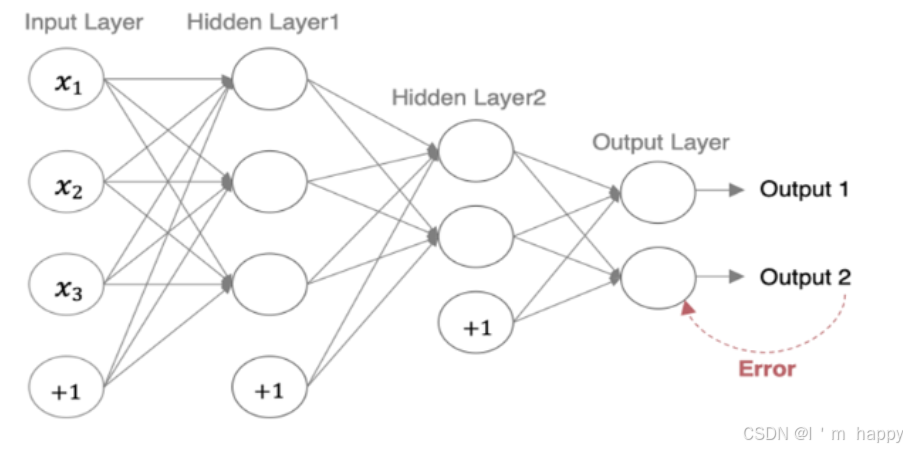
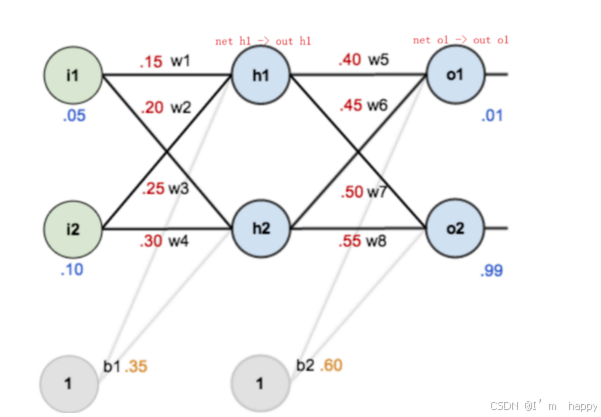
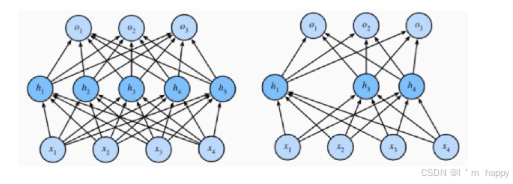
**反向传播对神经网络中的各个节点的权重进行更新.**一个简单的神经网络 用来举例:激活函数为sigmoid
前向传播运算过程:
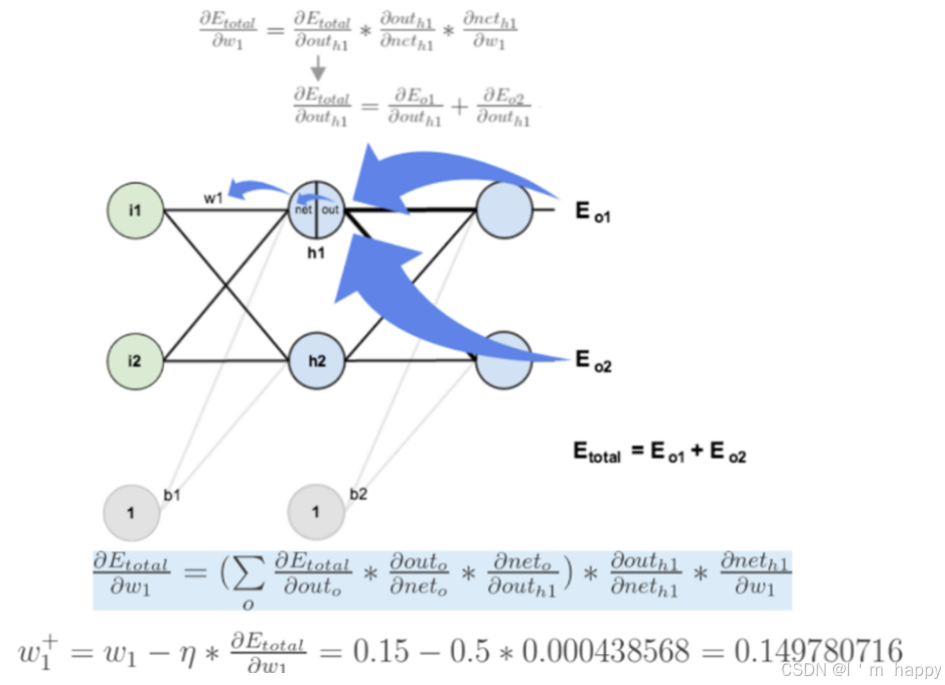
反向传播:我们先来求最简单的,求误差E对w5的导数。要求误差E对w5的导数,需要先求误差E对out o1的导数,再求out o1对net o1的导数,最后再求net o1对w5的导数,经过这个处理,我们就可以求出误差E对w5的导数(偏导),如下图所示:
导数(梯度)计算出来,下面就是反向传播与参数更新过程:
如果要想求误差E对W1的导数,误差E对W1的求导路径不止一条,计算过程如图所示:
- 代码实现
# 构建神经元网络
# 导入数据包
import torch
# 导入神经元nn模块
import torch.nn as nn
# 优化器
from torch import optim
# 创建神经元网络类
class Model(nn.Module):
# 初始化两个方法
# 初始化参数
def __init__(self):
# 调用父类初始化方法
super(Model, self).__init__()
# 构建网络层
self.linear1 = nn.Linear(2, 2)
self.linear2 = nn.Linear(2, 2)
# 初始化权重参数
nn.init.kaiming_normal_(self.linear1.weight)
nn.init.xavier_normal_(self.linear2.weight)
# 前向传播
def forward(self, x):
# 数据经过第一层网络
x = self.linear1(x)
# 计算第一层激活值
x = torch.relu(x)
# 数据经过第二层网络
x = self.linear2(x)
# 计算第二层激活值
x = torch.sigmoid(x)
return x
if __name__ == '__main__':
# 定义输入值和目标值
inputs = torch.tensor([[0.05, 0.10]])
target = torch.tensor([0.01, 0.99])
# 实例化神经元网络对象
model = Model()
# 预测值
output = model(inputs)
# 计算误差
loss = nn.MSELoss()
my_loss = loss(output, target)
print('loss', my_loss)
# 优化方法和反向传播方法
optimizer = optim.SGD(model.parameters(), lr=1e-2)
optimizer.zero_grad()
# 自己计算的损失函数进行反向传播
my_loss.backward()
print('梯度', model.linear1.weight.grad)
print('梯度', model.linear2.weight.grad)
optimizer.step()
# 打印神经网络参数
# state_dict():于获取模型参数状态字典的方法
print(model.state_dict())
总结
前向传播:指的就是数据输入的神经网络中,逐层向前传输,一直运算到输出层为止
反向传播(Back Propagation):利用损失函数ERROR,从后往前,结合梯度下降算法,一次求各个参数的偏导数
3.梯度下降优化方法
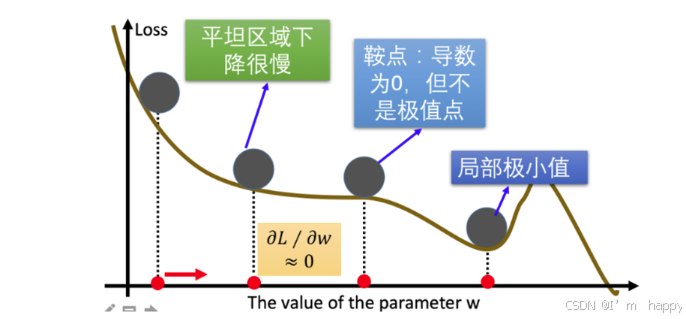
梯度下降优化算法中,可能碰到以下情况:
1.碰到平缓区域,梯度值较小,参数优化变慢
2.碰到’‘鞍点’',梯度为0,参数无法优化
3.碰到局部最小值,参数不是最优
对于以下问题,出现一些梯度下降算法的优化方法,例如: Monmentum,AdaGrad,RMSprop,Adqam等.
1.指数加权平均
指数移动加权平均则是参考各数值 ,并且各数值权重都不同,距离越远的数字对平均计算贡献越小,距离越近则对平均数的计算贡献越大.
计算公式为:
S t = { Y 1 , t = 0 β ∗ S t − 1 + ( 1 − β ) ∗ Y t t>0 S_t = \begin{cases} Y_1, & \text t =0 \\ β*S_{t-1} + (1-β)*Y_t & \text{t>0} \end{cases} St={Y1,β∗St−1+(1−β)∗Ytt=0t>0
St表示指数加权平均值
Yt表示t时刻的值
β 调节权重系数,该值越大平均数越平缓
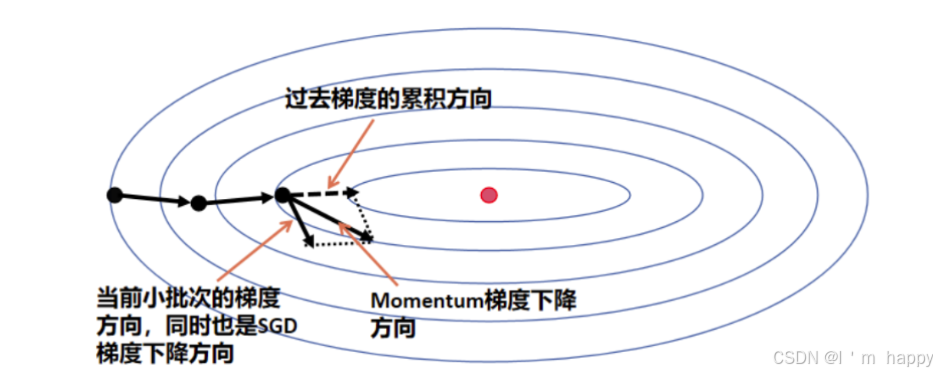
2.动量算法Momentum:
梯度计算公式:Dt = β * St-1 + (1- β) * Wt
梯度更新公式为:
St-1 表示历史梯度移动加权平均值
Wt 表示当前时刻的梯度值
Dt 为当前时刻的指数加权平均梯度值
β 为权重系数
假设:权重 β 为 0.9,例如:
- 第一次梯度值:D1 = S1 = W1
- 第二次梯度值:D2=S2 = 0.9 * S1 + W2 * 0.1
- 第三次梯度值:D3=S3 = 0.9 * S2 + W3 * 0.1
- 第四次梯度值:D4=S4 = 0.9 * S3 + W4 * 0.1
梯度下公式中的梯度计算,不在是当前时刻的t的梯度值,而是历史梯度值而历史梯度值的指数移动加权平均值,公式修改为:
W
i
j
n
e
w
=
W
i
j
o
i
d
−
α
D
t
W_{ij}^{new} = W_{ij}^{oid} - αD_t
Wijnew=Wijoid−αDt
Monmentum 优化方法是如何一定程度上克服 “平缓”、”鞍点” 的问题呢?
当处于鞍点位置时,由于当前的梯度为 0,参数无法更新。但是 Momentum 动量梯度下降算法已经在先前积累了一些梯度值,很有可能使得跨过鞍点
由于 mini-batch 普通的梯度下降算法,每次选取少数的样本梯度确定前进方向,可能会出现震荡,使得训练时间变长。Momentum 使用移动加权平均,平滑了梯度的变化,使得前进方向更加平缓,有利于加快训练过程。
import torch
import matplotlib.pyplot as plt
def test03():
# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()
# 2 实例化优化方法,SGD指定参数beta=0.9
optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)
# 3 第一次更新计算梯度,并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f,更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度,并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy())
3.AdaGrad:通过对不同的参数分量使用不同的学习率,AdaGrad学习率总体会逐渐减小
计算步骤如下:
import torch
import matplotlib.pyplot as plt
def test04():
# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()
# 2 实例化优化方法:adagrad优化方法
optimizer = torch.optim.Adagrad([w], lr=0.01)
# 3 第1次更新 计算梯度,并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度,并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
1.初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6(表示为10的-6次方)
2.初始化梯度累积变量 s = 0
3.从训练集中采样 m 个样本的小批量,计算梯度 g
4.累积平方梯度 s = s + g ⊙ g,⊙ 表示各个分量相乘
学习率计算α的计算公式为:
α
=
α
s
+
σ
α = \frac{α}{\sqrt{s} + σ}
α=s+σα
参数更新公式为:
w
=
w
−
α
s
+
σ
w = w - \frac{α}{\sqrt{s} + σ}
w=w−s+σα
注:AdaGrad缺点是可能使得学习率过早,过量的降低,导致模型 训练到后期学习率太小,难以找到最优解.
4.RMSProp
RMSProp优化算法是对AdaGrad的优化,使用指数移动加权平均梯度替换历史梯度的平方和,计算如下:
# alpha=0.9 初始化β权重系数
"""
初始化学习率 α、初始化参数 θ、小常数 σ = 1e-6
初始化参数 θ
初始化梯度累计变量 s
从训练集中采样 m 个样本的小批量,计算梯度 g
使用指数移动平均累积历史梯度,
"""
公式如下:
s
=
β
∗
s
+
(
1
−
β
)
g
⊙
g
(
⊙
表示各个分量相乘
)
s = β*s + (1-β)g⊙g (⊙ 表示各个分量相乘)
s=β∗s+(1−β)g⊙g(⊙表示各个分量相乘)
学习率计算公式为:
α
=
α
s
+
σ
α = \frac{α}{\sqrt{s} + σ}
α=s+σα
参数更新公式为:
w
=
w
−
α
s
+
σ
.
g
w = w - \frac{α}{\sqrt{s} + σ}.g
w=w−s+σα.g
import torch
import matplotlib.pyplot as plt
def test05():
# 1 初始化权重参数
w = torch.tensor([1.0], requires_grad=True, dtype=torch.float32)
y = ((w ** 2) / 2.0).sum()
# 2 实例化优化方法:RMSprop算法,其中alpha对应这beta
optimizer = torch.optim.RMSprop([w], lr=0.01, alpha=0.9)
# 3 第1次更新 计算梯度,并对参数进行更新
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第1次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
# 4 第2次更新 计算梯度,并对参数进行更新
# 使用更新后的参数机选输出结果
y = ((w ** 2) / 2.0).sum()
optimizer.zero_grad()
y.backward()
optimizer.step()
print('第2次: 梯度w.grad: %f, 更新后的权重:%f' % (w.grad.numpy(), w.detach().numpy()))
5.Adam:使用动量和RMSProp来动态调整每个参数的学习率
- Momentum使用指数加权平均计算当前梯度值
- AdaGrad , RMSProp 使用自适应的学习率
- Adam优化算法将Momentum 和RMSProp算法结合一起
- 修正梯度:使用梯度的指数加权平均
- 修正学习率:使用梯度平方的指数加权平均
# 2 实例化优化方法:Adam算法,其中betas是指数加权的系数
optimizer = torch.optim.Adam([w], lr=0.01, betas=[0.9, 0.99])
4.学习率衰减方法
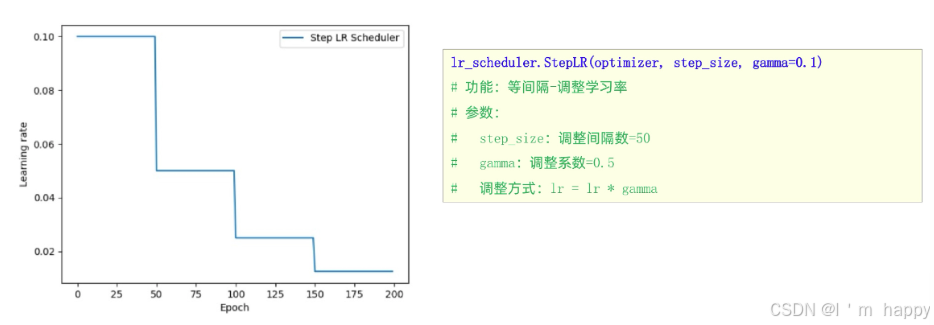
1.等间隔学习率衰减
学习率衰减方法-等间隔学习率衰减
如图所示
def test_StepLR():
# 0.参数初始化
LR = 0.1 # 设置学习率初始化值为0.1
iteration = 10
max_epoch = 200
# 1 初始化参数
y_true = torch.tensor([0])
x = torch.tensor([1.0])
w = torch.tensor([1.0], requires_grad=True)
# 2.优化器
optimizer = optim.SGD([w], lr=LR, momentum=0.9)
# 3.设置学习率下降策略
scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.5)
# 4.获取学习率的值和当前的epoch
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_last_lr()) # 获取当前lr
epoch_list.append(epoch) # 获取当前的epoch
for i in range(iteration): # 遍历每一个batch数据
loss = ((w*x-y_true)**2)/2.0 # 目标函数
optimizer.zero_grad()
# 反向传播
loss.backward()
optimizer.step()
# 更新下一个epoch的学习率
scheduler_lr.step()
# 5.绘制学习率变化的曲线
plt.plot(epoch_list, lr_list, label="Step LR Scheduler")
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
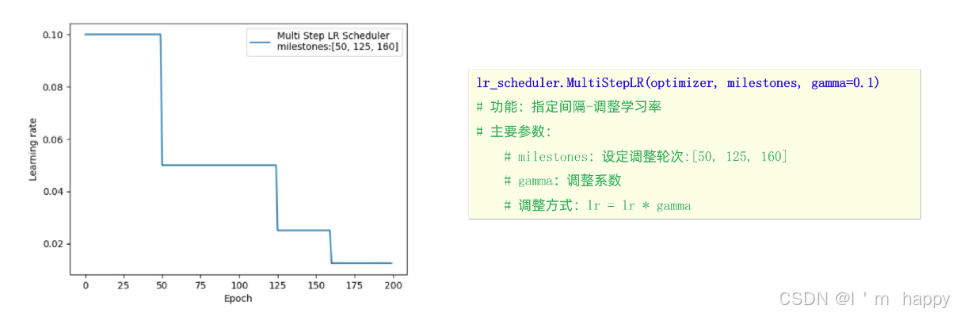
2.指定间隔学习率衰减
学习率优化方法-指定间隔学习率衰减
如图所示
def test_MultiStepLR():
torch.manual_seed(1)
LR = 0.1
iteration = 10
max_epoch = 200
weights = torch.randn((1), requires_grad=True)
target = torch.zeros((1))
print('weights--->', weights, 'target--->', target)
optimizer = optim.SGD([weights], lr=LR, momentum=0.9)
# 设定调整时刻数
milestones = [50, 125, 160]
# 设置学习率下降策略
scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.5)
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_last_lr())
epoch_list.append(epoch)
for i in range(iteration):
loss = torch.pow((weights - target), 2)
optimizer.zero_grad()
# 反向传播
loss.backward()
# 参数更新
optimizer.step()
# 更新下一个epoch的学习率
scheduler_lr.step()
plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler\nmilestones:{}".format(milestones))
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
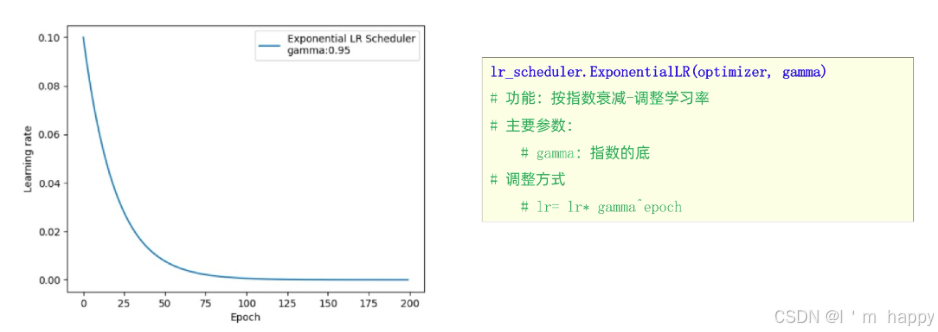
3.按指数学习率衰减
学习率优化方法-按指数学习率衰减
如图所示
def test_ExponentialLR():
# 0.参数初始化
LR = 0.1 # 设置学习率初始化值为0.1
iteration = 10
max_epoch = 200
# 1 初始化参数
y_true = torch.tensor([0])
x = torch.tensor([1.0])
w = torch.tensor([1.0], requires_grad=True)
# 2.优化器
optimizer = optim.SGD([w], lr=LR, momentum=0.9)
# 3.设置学习率下降策略
gamma = 0.95
scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)
# 4.获取学习率的值和当前的epoch
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_last_lr())
epoch_list.append(epoch)
for i in range(iteration): # 遍历每一个batch数据
loss = ((w * x - y_true) ** 2) / 2.0
optimizer.zero_grad()
# 反向传播
loss.backward()
optimizer.step()
# 更新下一个epoch的学习率
scheduler_lr.step()
# 5.绘制学习率变化的曲线
plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler")
plt.xlabel("Epoch")
plt.ylabel("Learning rate")
plt.legend()
plt.show()
3.正则化方法
正则化作用:防止神经网络表示过拟合
Dropout(随机失活)
在神经网络中模型参数较多,在数据不足的情况下,容易过拟合,**Dropout(随机失活)**是一个简单有效的正则化方法.
在训练过程中,Dropout的实现是让神经元 以超参数p的概率停止工作或者 激活被置为0,未被置为0的进行缩放,缩放比例为1/(1-p)
在测试过程中,随机失活不起作用
import torch
import torch.nn as nn
def test():
# 初始化随机失活层
dropout = nn.Dropout(p=0.4)
# 初始化输入数据:表示某一层的weight信息
inputs = torch.randint(0, 10, size=[1, 4]).float()
layer = nn.Linear(4,5)
y = layer(inputs)
print("未失活FC层的输出结果:\n", y)
y = dropout(y)
print("失活后FC层的输出结果:\n", y)
# 上述代码将 Dropout 层的概率 p 设置为 0.4,此时经过 Dropout 层计算的张量中就出现了很多 0 , 未变为0的按照(1/(1-0.4))进行处理。