RNN模型介绍
1.RNN模型介绍
1.1什么是RNN模型
RNN模型:循环神经网络,以序列数据为输出,通过网络内部设计有效捕捉序列之间关系特征,一般序列特征进行输出
-
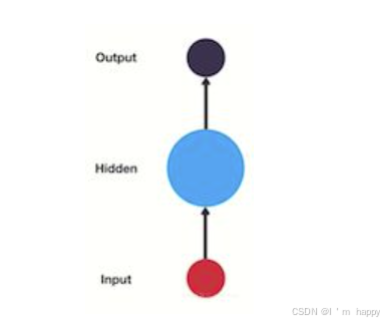
单层神经网络结构;
-
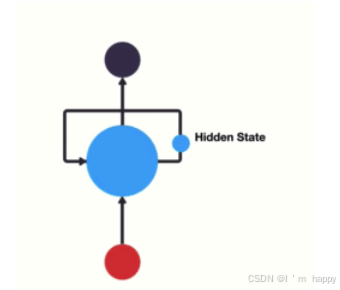
RNN单层网络结构:
-
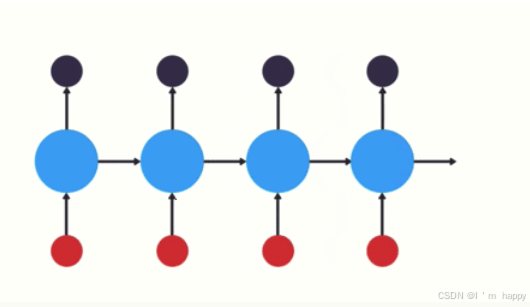
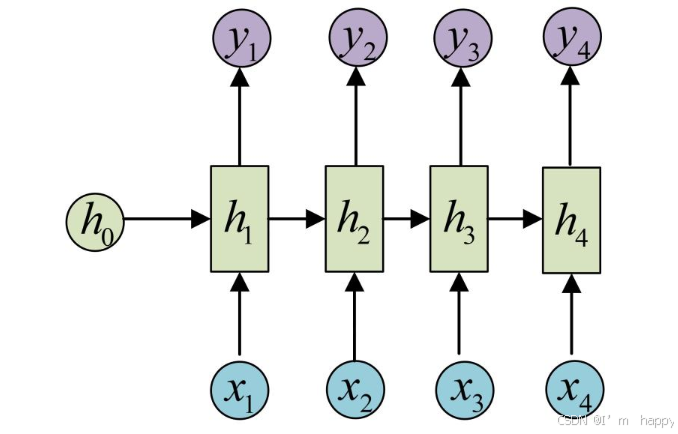
以时间步对RNN展开单层网络结构:
解析:
RNN模型使隐层上一个时间步产生的结果能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上步隐层输出)对当下时间步产生影响
1.2RNN模型作用
RNN结构能够很好利用序列之间的关系,因此针对自然界连续性的输入序列,如:人类语言,语音等,广泛应用于NLP领域,如文本分类,情感分析,意图识别等
-
举例说明:
-
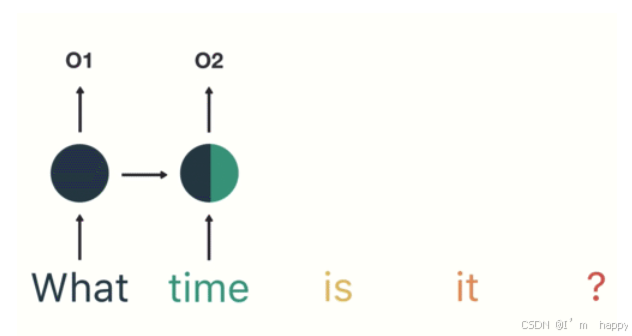
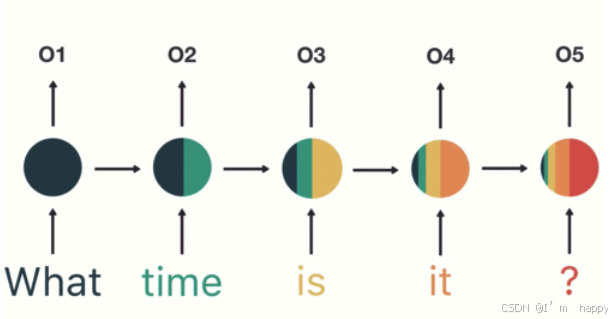
第一步:用户输入了"What time is it ?", 我们首先需要对它进行基本的分词, 因为RNN是按照顺序工作的, 每次只接收一个单词进行处理.
- 第二步:首先将单词"What"输送给RNN, 它将产生一个输出O1.
- 第三步: 继续将单词"time"输送给RNN, 但此时RNN不仅仅利用"time"来产生输出O2, 还会使用来自上一层隐层输出O1作为输入信息.
- 第四步:重复这样步骤,知道处理完所有单词
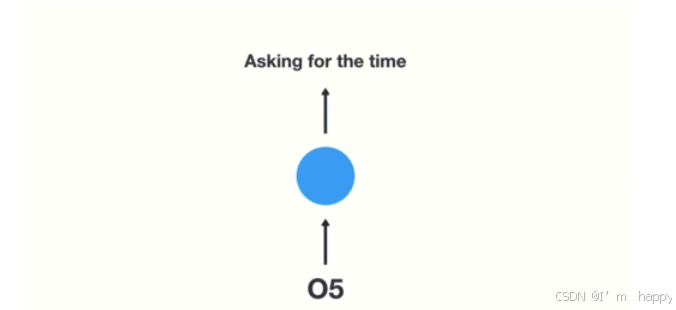
- 第五步:将最终的隐层输出05进行处理来解析用户意图
1.3RNN模型分类
-
按照输入和输出结构分类
-
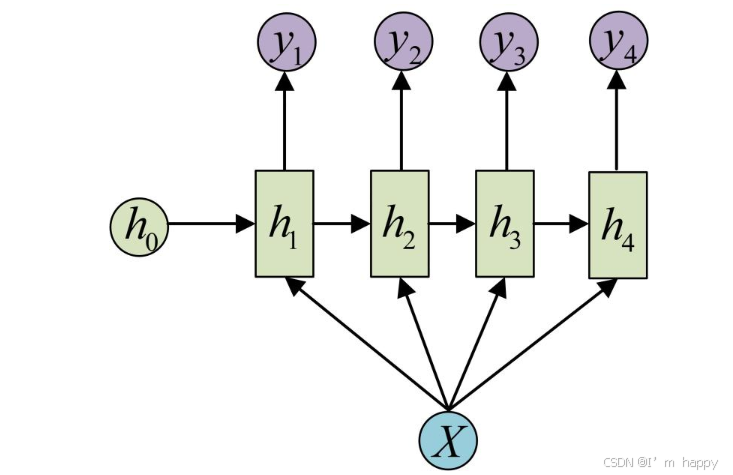
N vs N:输入和输出等长,可用于生成等长度的合辙诗句
-
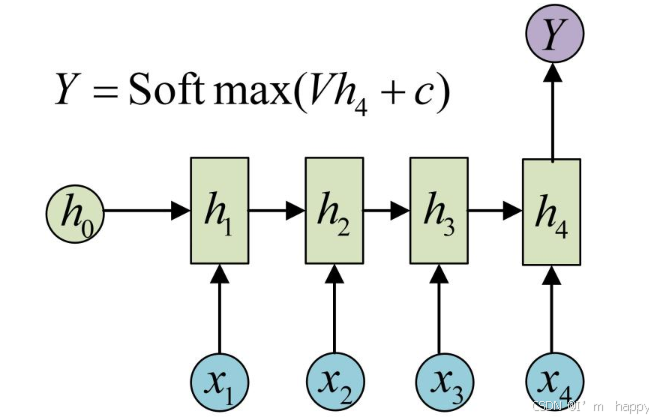
N vs1:要求输出的是一个单独的值而不是序列,在最后一个隐藏层h上进行线性变换,还可明确使用sigmoid(多分类多标签)或则softmax进行处理
-
**1 vs N:**可用于将图片生层文字
<img
-
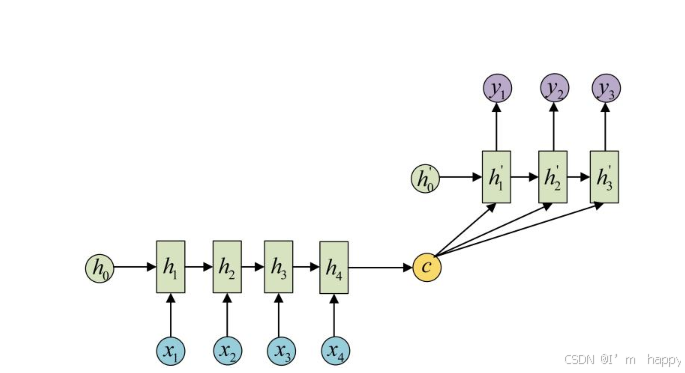
N vs M:由编码器和解码器组成,可称为:seq2seq(序列到序列) 输入数据首先通过编码器, 输出一个隐含变量c, 最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上, 保证输入信息被有效利用.
-
-
按照RNN内部构造进行分类
-
传统RNN
-
LSTM
-
Bi-LSTM
-
GRU
-
Bi-GRU
2.传统RNN模型
2.1RNN结构图
1.内部结构分析
输入由两部分为:h(t-1)上一个时间步的隐层输出和x(t)此时间步输入,到RNN内部融合到一起后,形成新的张量[x(t),h(t-)],通过一个全连接线性层使用tanh激活函数,得到该时间步输出h(t),将下一个时间步的输入和x(t-1)一起进入到结构体中,以此类推
- 过程演示
计算公式
h
t
=
tanh
(
x
t
W
i
h
T
+
b
i
h
+
h
t
−
1
W
h
h
T
+
b
h
h
)
h_t = \tanh(x_t W_{ih}^T + b_{ih} + h_{t-1}W_{hh}^T + b_{hh})
ht=tanh(xtWihT+bih+ht−1WhhT+bhh)
- 激活函数tanh:用于调节流经网络的值,将值压缩到-1和1之间
2.使用Pytorch构建RNN模型
def dem_rnn_for_first():
# rnn 参数说明
# 输入维度:5
# 输出维度:6
# 隐藏层维度:2
# batch_first = True 是否交换输入和批次维度,默认为False
# bidirectional = True 双向循环神经网络,默认为False
rnn = nn.RNN(5, 6, 1, batch_first=True,bidirectional=True)
# 查看参数
# all_weights:包含两个元素,第一个元素是输入门参数,第二个元素是输出门参数
print(rnn.all_weights)
print(rnn.all_weights[0][0].shape)
print(rnn.all_weights[0][1].shape)
# input参数:(seq_len, batch, input_size)
input = torch.randn(3, 20, 5)
h0 = torch.randn(2, 3, 6)
out, hn = rnn(input, h0)
print(out.shape)
print(hn.shape)
2.2RNN优缺点
优势:
内部结构简单,对资源要求低,在短序列任务上性能和效果优异
缺点:
在进行反向传播时,多长的序列会导致梯度计算异常,发生梯度爆炸或消失
梯度消失或爆炸
sigmoid导数值域是固定的在[0,0.25]而公式中w也小于1,通过公式后最后的结果会非常小,被称为梯度消失,如果我们人为增大w的值,使其大于1,那么连乘后的造成的梯度过大,称为梯度爆炸.
3.LSTM模型
3.1什么是LSTM模型
LSTM模型:长短时记忆网络:为RNN变体,能有效捕捉长序列之间的语义关联,缓解梯度消失或爆炸现象,核心结构分为
- 遗忘门
- 输入门
- 输出门
- 细胞结构
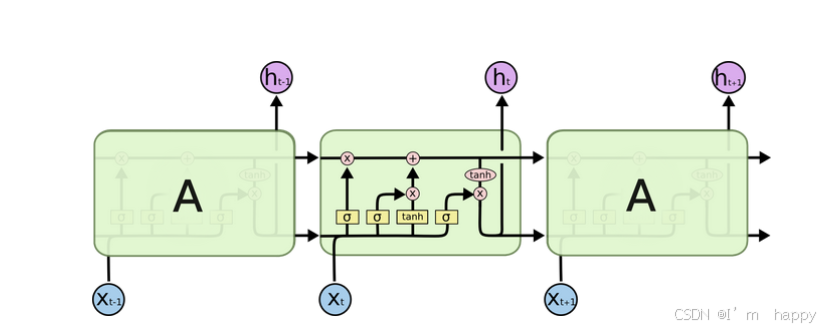
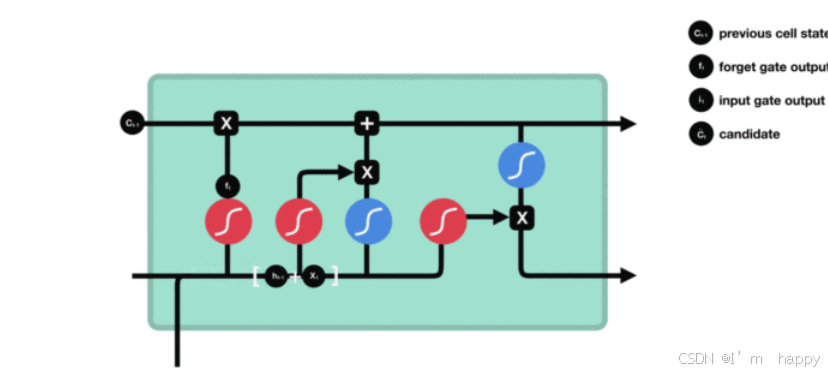
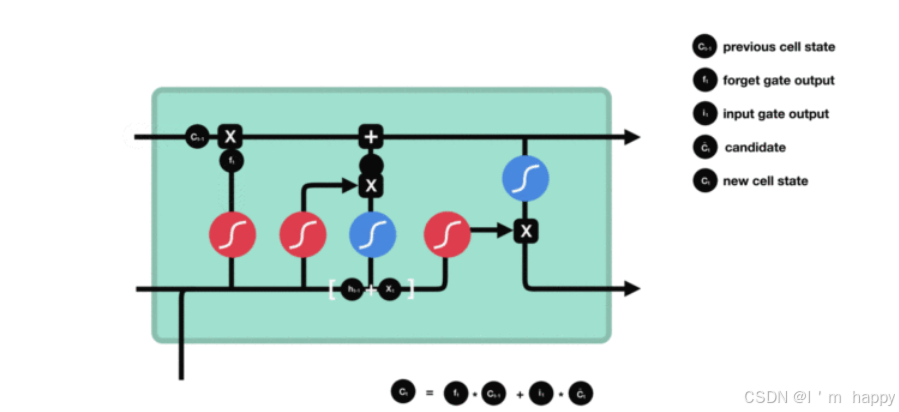
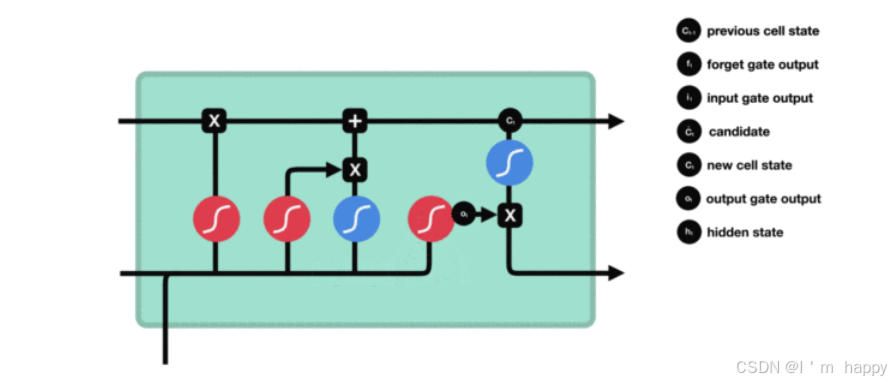
3.2LSTM内部结构图
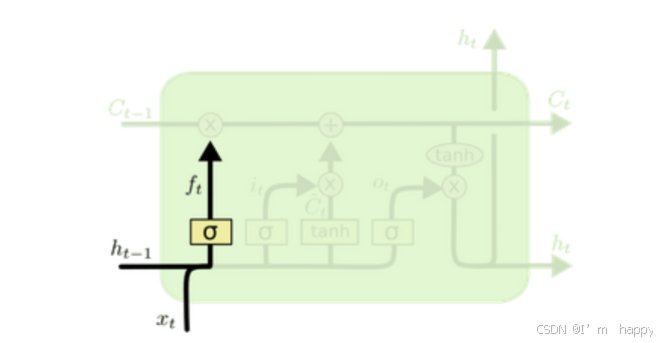
- 遗忘门结构分析
将当前时间输入x(t)与上一个时间步隐含状态h(t-1)拼接,得到通过线性层做变换,以及sigmoid函数激活得到f(t),遗忘门作用的是上一层细胞状态上,代表遗忘多少信息,由x(t),h(t-1),计算得到,以及计算携带多少信息
计算公式:
f
t
=
σ
(
W
i
f
x
t
+
b
i
f
+
W
h
f
h
t
−
1
+
b
h
f
)
f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\
ft=σ(Wifxt+bif+Whfht−1+bhf)
内部结构演示
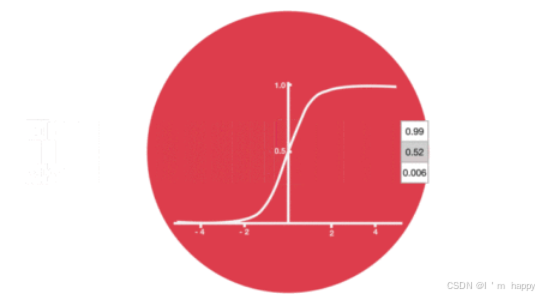
经过激活函数sigmoid作用:将数据压缩到0和1之间
- 输出门部分结构与计算公式
计算公式:
i
t
=
σ
(
W
i
i
x
t
+
b
i
i
+
W
h
i
h
t
−
1
+
b
h
i
)
i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\
it=σ(Wiixt+bii+Whiht−1+bhi)
结构分析
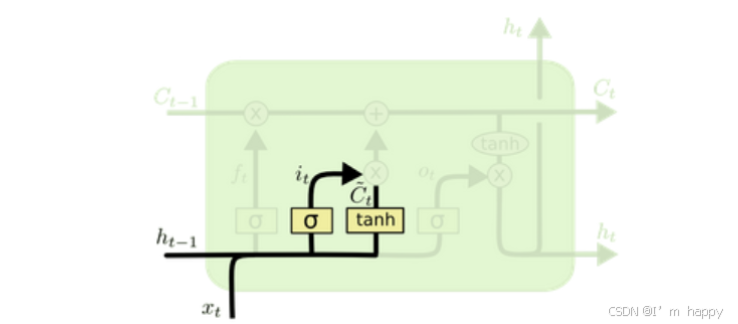
看到输入门的计算公式有两个, 第一个就是产生输入门门值的公式, 它和遗忘门公式几乎相同, 区别只是在于它们之后要作用的目标上. 输入信息有多少需要进行过滤. 对于LSTM来讲, 它得到的是当前的细胞状态, 而不是像经典RNN一样得到的是隐含状态.
输入门内部结构演示
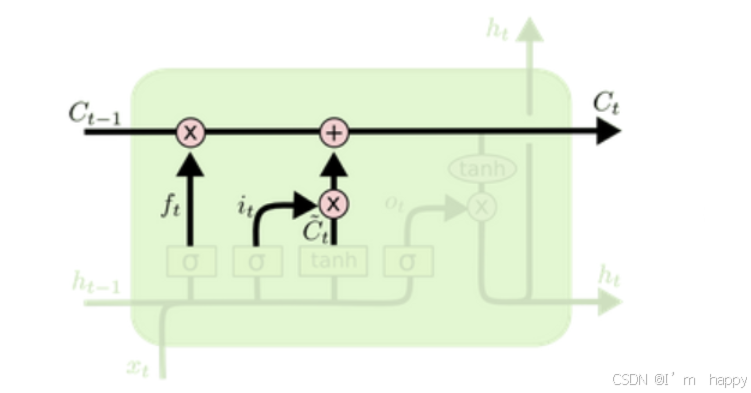
- 细胞状态更新分析
将得到的遗忘门的值和上一个时间步的到的C(t-1)相乘,加上输入门门值与当前时间步得到的未更新C(t)相乘的结果. 最终得到更新后的C(t)作为下一个时间步输入的一部分.
计算公式
c
t
=
f
t
⊙
c
t
−
1
+
i
t
⊙
g
t
c_t = f_t \odot c_{t-1} + i_t \odot g_t \\
ct=ft⊙ct−1+it⊙gt
细胞状态更新过程
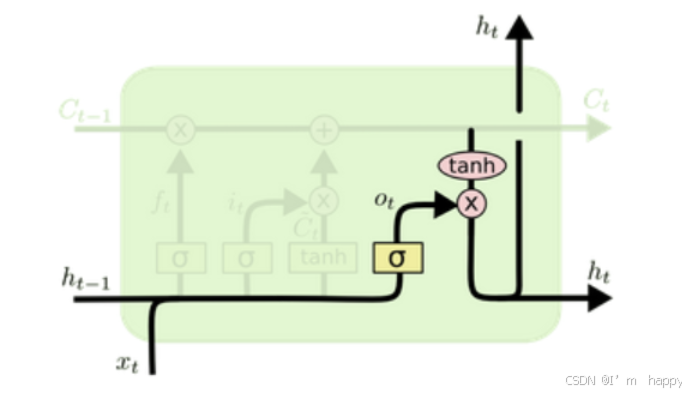
- 输出门部分结构图
结构分析
- 输出门部分的公式也是两个, 第一个即是计算输出门的门值, 它和遗忘门,输入门计算方式相同. 第二个即是使用这个门值产生隐含状态h(t), 他将作用在更新后的细胞状态C(t)上, 并做tanh激活, 最终得到h(t)作为下一时间步输入的一部分. 整个输出门的过程, 就是为了产生隐含状态h(t).
计算公式
o
t
=
σ
(
W
i
o
x
t
+
b
i
o
+
W
h
o
h
t
−
1
+
b
h
o
)
o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\
ot=σ(Wioxt+bio+Whoht−1+bho)
h t = o t ⊙ tanh ( c t ) h_t = o_t \odot \tanh(c_t) \\ ht=ot⊙tanh(ct)
输出们演示过程
3.3使用Pytorch构建LSTM模型
BI-LSTM 两次得到的LSTM结果进行拼接作为最终输出.
-
参数说明
-
nn.LSTM类初始化主要参数解释:
- input_size: 输入张量x中特征维度的大小.
- hidden_size: 隐层张量h中特征维度的大小.
- num_layers: 隐含层的数量.
- bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
- batch_first = True 是否交换输入和批次维度,默认为False
-
nn.LSTM类实例化对象主要参数解释:
- input: 输入张量x.
- h0: 初始化的隐层张量h.
- c0: 初始化的细胞状态张量c.
-
nn.LSTM使用示例:
def dm_lstm_first():
lstm = nn.LSTM(5, 6, 1, batch_first=True, bidirectional=True)
input = torch.randn(4, 2, 5)
h0 = torch.randn(2, 4, 6)
c0 = torch.randn(2, 4, 6)
out, (hn, cn) = lstm(input, (h0, c0))
print(out)
print(out.shape)
print(hn)
print(hn.shape)
print(cn)
print(cn.shape)
3.4LSTM优缺点
LSTM优势:
有效减缓长序列中出现的梯度消失或爆炸,在更长序列问题优于传统RNN
缺点
内部结构相对复杂,训练效率在同等算力要低于RNN
4.GRU模型
4.1什么是GRU模型
GRU称为门控制单元结构,同LStm一样有效捕捉长序列之间的语义关联,缓解梯度消失或爆炸的可能,结构与计算要比LSTM简单,核心结构分为:
- 更新门
- 重置门
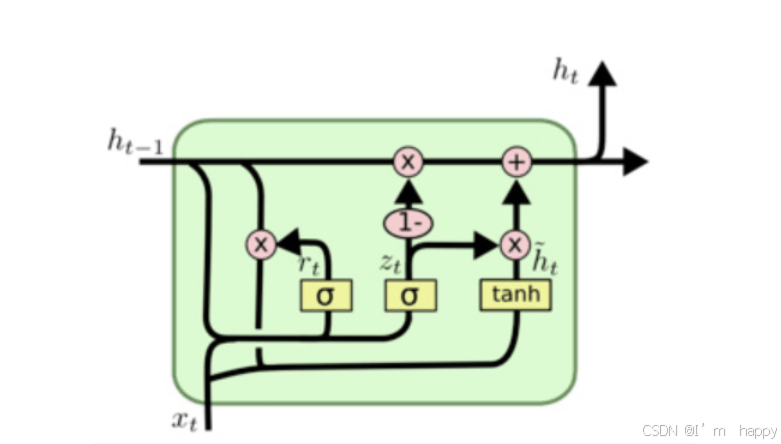
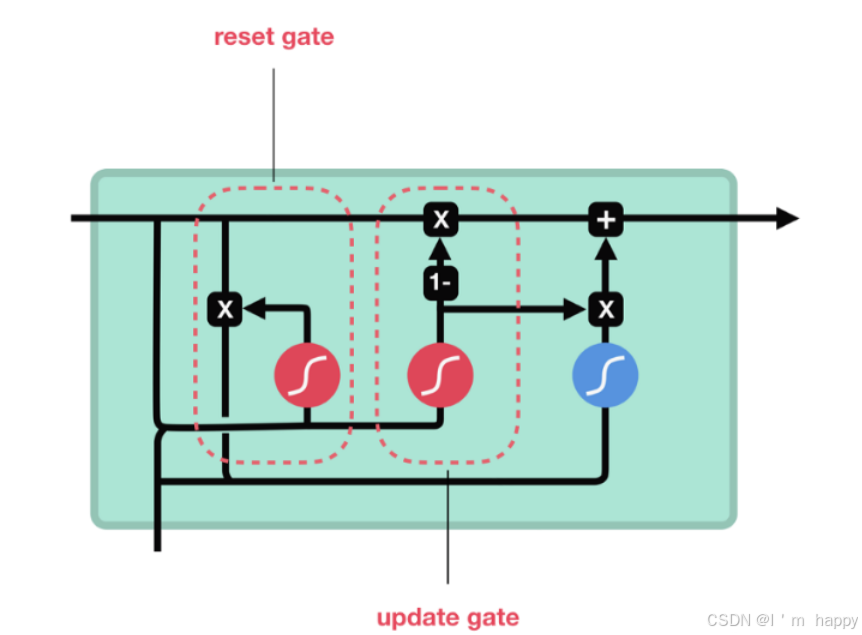
4.2GRU内部图
结构分析
计算更新门和重置门的门值,分别计算Z(t)和r(t),使用X(t)与h(t-)拼接进行线性变换,在经过sigmoid激活,表示上一个时间步传来的信息有多少被利用,接着使用重置后的h(t-1)与当前时间步x(t)拼接线性变换经过tanh的h(t),1-门值会作用在h(t-1)上, 随后将两者的结果相加, 得到最终的隐含状态输出h(t), 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的h(t), 而当门值趋于0时, 输出就是上一时间步的h(t-1).
计算公式
r
t
=
σ
(
W
i
r
x
t
+
b
i
r
+
W
h
r
h
(
t
−
1
)
+
b
h
r
)
z
t
=
σ
(
W
i
z
x
t
+
b
i
z
+
W
h
z
h
(
t
−
1
)
+
b
h
z
)
n
t
=
tanh
(
W
i
n
x
t
+
b
i
n
+
r
t
∗
(
W
h
n
h
(
t
−
1
)
+
b
h
n
)
)
h
t
=
(
1
−
z
t
)
∗
n
t
+
z
t
∗
h
(
t
−
1
)
r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr} h_{(t-1)} + b_{hr}) \\ z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz} h_{(t-1)} + b_{hz}) \\ n_t = \tanh(W_{in} x_t + b_{in} + r_t * (W_{hn} h_{(t-1)}+ b_{hn})) \\ h_t = (1 - z_t) * n_t + z_t * h_{(t-1)}
rt=σ(Wirxt+bir+Whrh(t−1)+bhr)zt=σ(Wizxt+biz+Whzh(t−1)+bhz)nt=tanh(Winxt+bin+rt∗(Whnh(t−1)+bhn))ht=(1−zt)∗nt+zt∗h(t−1)
4.3使用Pytorch构建GRU模型
-
参数说明
-
nn.GRU类初始化主要参数解释:
- input_size: 输入张量x中特征维度的大小.
- hidden_size: 隐层张量h中特征维度的大小.
- num_layers: 隐含层的数量.
- bidirectional: 是否选择使用双向LSTM, 如果为True, 则使用; 默认不使用.
-
nn.GRU类实例化对象主要参数解释:
- input: 输入张量x.
- h0: 初始化的隐层张量h.
def dm_gru():
gru = nn.GRU(4, 5, 1, batch_first=True, bidirectional=True)
input = torch.randn(2, 4, 4)
h0 = torch.randn(2, 2, 5)
out, hn = gru(input, h0)
print(out)
print(out.shape)
print(hn)
print(hn.shape)
4.4GRU优势
优势
GRU和LSTM在捕捉长序列语义关联时,能有效抑制梯度消失或爆炸,效果优于RNN其计算复杂度相比于LSTM要小
缺点
- GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈.