前言:
在最近发布的两篇文章中,我们讲了两种判断矩阵是否可逆的方法,我们提到了矩阵的逆,那么很自然的就能想到,如何求解矩阵的逆,这篇文章中将会给出答案!
一、线性代数知识回顾:
1. 如果矩阵可逆,那么矩阵的逆是唯一的
这个简单的定理我们给出证明:(一些证明起来比较麻烦的定理我们一般不给出证明)
若 n 阶矩阵
可逆,记
的一个逆为
,另一个逆为
,则:
由此可见,
的逆唯一,因此我们可以记为
2. n 阶矩阵 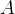
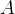
(其中
为初等矩阵,
)
3. 对矩阵左乘单位矩阵就相当于对矩阵做一次初等行变换
4. 若矩阵 A 可逆 ,则可以经过一系列初等行变换将其化为单位矩阵。见下面推理(重点)
若矩阵
可逆,则根据上面第二条,存在初等矩阵
(
)使得:
(1)
由于初等矩阵都是可逆的,则:
(2)
而初等矩阵的逆仍为初等矩阵,根据上面第三条,我们知道,对矩阵
做一系列初等行变换可以化为单位矩阵,定理得证。不过我们仍然要继续推理一下:
将上式继续变化得到:
(3)
根据(2)(3)式可知,对可逆矩阵
作一系列初等行变换将其化为单位矩阵
,对单位矩阵做同样的初等行变换可以将单位矩阵化为
,这便给出了一个求矩阵的逆的方法!
二、算法描述:
我们知道了方法后想一想,如何将一个可逆矩阵通过初等行变换化为单位矩阵呢?
我们只需将矩阵自上向下地化为上三角矩阵,然后每一行除一个非零常数使得主对角线元素为 1 (也可以化好一行后将这一行除以一个非零常数使得这一行中位于主对角线上的元素的值为 1,也就是先将矩阵化为单位上三角矩阵),然后自下向上将矩阵主对角线以上的元素全部化为 0 即可,并且对该矩阵做的每一步变换都要对单位矩阵做相同的变换,最后即可将单位矩阵化为所求矩阵的逆!
三、代码实现:
类定义:(若有人不太了解类,也请往下看,不要被这个吓住了,程序的核心是算法!)
class Mat
{
public:
int m = 1, n = 1; //行数和列数
double mat[N][N] = { 0 }; //矩阵开始的元素
Mat() {}
Mat(int mm, int nn)
{
m = mm; n = nn;
}
void create();//创建矩阵
void Print();//打印矩阵
void eye();//令矩阵行列下标相同时值为 1,不同时为 0
bool inv(Mat a);//求矩阵的逆
};其中,eye函数主要是为了方便定义单位矩阵,其代码如下:
void Mat::eye()
{
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j)
mat[i][j] = 1;
else
mat[i][j] = 0;
}
}
}重头戏!!!求矩阵的逆的函数 inv(Mat a)即将登场,我们这个函数其实本身也可以判断是否是可逆矩阵,这里面融合判断可逆的方法,因为如果先判断是否可逆,如果可逆再求逆,那么这样其实是多余进行了好多次行变换,我们这样直接融合判断可逆和求解逆矩阵为一体的函数更加省时。
代码如下:
bool Mat::inv(Mat a)
{
if (a.n != a.m)
{
cout << "不可逆!" << endl;
return false;
}
m = a.m; n = a.n;
eye(); //创建单位矩阵
//下来进行自上而下的初等行变换,使得矩阵 a.mat 变成单位上三角矩阵
for (int i = 1; i <= m; i++) //注意这里要 i<=m,和之前的上三角矩阵有不同
{ //因为要判断最后一行化为上三角矩阵的最后一行最后一列元素是否为 0
//寻找第 i 列不为零的元素
int k;
for (k = i; k <= m; k++)
{
if (fabs(a.mat[k][i]) > 1e-10) //满足这个条件时,认为这个元素不为0
break;
}
if (k <= m)//说明第 i 列有不为0的元素
{
if (k != i)//说明第 i 行 第 i 列元素为零,需要和其他行交换
{
//交换第 i 行和第 k 行所有元素
for (int j = 1; j <= n; j++)//需从第一个元素交换,注意与之前化上三角矩阵不同
{//使用mat[0][j]作为中间变量交换元素,两个矩阵都要交换
a.mat[0][j] = a.mat[i][j]; a.mat[i][j] = a.mat[k][j]; a.mat[k][j] = a.mat[0][j];
mat[0][j] = mat[i][j]; mat[i][j] = mat[k][j]; mat[k][j] = mat[0][j];
}
}
double b = a.mat[i][i];//倍数
//将矩阵 a.mat 的主对角线元素化为 1
for (int j = 1; j <= n; j++)//从第一个元素开始
{
a.mat[i][j] /= b;
mat[i][j] /= b;
}
for (int j = i + 1; j <= m; j++)
{
//注意本来为 -a.mat[j][i]/a.mat[i][i],因为a.mat[i][i]等于 1,则不需要除它
b = -a.mat[j][i];
for (k = 1; k <= n; k++)
{
a.mat[j][k] += b * a.mat[i][k];//第 i 行 b 倍加到第 j 行
mat[j][k] += b * mat[i][k];
}
}
}
else
{
cout << "不可逆!" << endl;
return false;
}
}
//下面进行自下而上的行变换,将 a.mat 矩阵化为单位矩阵
for (int i = m; i > 1; i--)
{
for (int j = i - 1; j >= 1; j--)
{
double b = -a.mat[j][i];
a.mat[j][i] = 0; //实际上是通过初等行变换将这个元素化为 0,
for (int k = 1; k <= n; k++)
{//通过相同的初等行变换来变换右边矩阵
mat[j][k] += b * mat[i][k];
}
}
}
return true;
}今天我们探讨了矩阵求逆的方法,逆矩阵的概念在线性代数里面十分重要,希望大家可以认真对待线性代数,适当了解其中的原理,不要只记结论,大家坚持下去就会慢慢体会到自己思维的提升!下一篇文章我们将在可逆的基础上定义矩阵的除法,可逆矩阵可以作为分母,就像实数里面非零数可以作为分母一样。最后我们附上完整代码:
#include<iostream>
#include <cmath>
#define N 10
using namespace std;
class Mat
{
public:
int m = 1, n = 1; //行数和列数
double mat[N][N] = { 0 }; //矩阵开始的元素
Mat() {}
Mat(int mm, int nn)
{
m = mm; n = nn;
}
void create();//创建矩阵
void Print();//打印矩阵
void eye();//令矩阵行列下标相同时值为 1,不同时为 0
bool inv(Mat a);//求矩阵的逆
};
void Mat::create()
{
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
cin >> mat[i][j];
}
}
}
void Mat::Print()
{
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
cout << mat[i][j] << "\t";
}
cout << endl;
}
}
void Mat::eye()
{
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
if (i == j)
mat[i][j] = 1;
else
mat[i][j] = 0;
}
}
}
bool Mat::inv(Mat a)
{
if (a.n != a.m)
{
cout << "不可逆!" << endl;
return false;
}
m = a.m; n = a.n;
eye(); //创建单位矩阵
//下来进行自上而下的初等行变换,使得矩阵 a.mat 变成单位上三角矩阵
for (int i = 1; i <= m; i++) //注意这里要 i<=m,和之前的上三角矩阵有不同
{ //因为要判断最后一行化为上三角矩阵的最后一行最后一列元素是否为 0
//寻找第 i 列不为零的元素
int k;
for (k = i; k <= m; k++)
{
if (fabs(a.mat[k][i]) > 1e-10) //满足这个条件时,认为这个元素不为0
break;
}
if (k <= m)//说明第 i 列有不为0的元素
{
if (k != i)//说明第 i 行 第 i 列元素为零,需要和其他行交换
{
//交换第 i 行和第 k 行所有元素
for (int j = 1; j <= n; j++)//需从第一个元素交换,注意与之前化上三角矩阵不同
{//使用mat[0][j]作为中间变量交换元素,两个矩阵都要交换
a.mat[0][j] = a.mat[i][j]; a.mat[i][j] = a.mat[k][j]; a.mat[k][j] = a.mat[0][j];
mat[0][j] = mat[i][j]; mat[i][j] = mat[k][j]; mat[k][j] = mat[0][j];
}
}
double b = a.mat[i][i];//倍数
//将矩阵 a.mat 的主对角线元素化为 1
for (int j = 1; j <= n; j++)//从第一个元素开始
{
a.mat[i][j] /= b;
mat[i][j] /= b;
}
for (int j = i + 1; j <= m; j++)
{
//注意本来为 -a.mat[j][i]/a.mat[i][i],因为a.mat[i][i]等于 1,则不需要除它
b = -a.mat[j][i];
for (k = 1; k <= n; k++)
{
a.mat[j][k] += b * a.mat[i][k];//第 i 行 b 倍加到第 j 行
mat[j][k] += b * mat[i][k];
}
}
}
else
{
cout << "不可逆!" << endl;
return false;
}
}
//下面进行自下而上的行变换,将 a.mat 矩阵化为单位矩阵
for (int i = m; i > 1; i--)
{
for (int j = i - 1; j >= 1; j--)
{
double b = -a.mat[j][i];
a.mat[j][i] = 0; //实际上是通过初等行变换将这个元素化为 0,
for (int k = 1; k <= n; k++)
{//通过相同的初等行变换来变换右边矩阵
mat[j][k] += b * mat[i][k];
}
}
}
return true;
}
int main()
{
Mat a(3, 3);
cout << "请输入 " << a.m << "*" << a.n << " 的矩阵:" << endl;
a.create();
Mat b;
if (b.inv(a))
b.Print();
return 0;
}如有不足之处,欢迎大家指正!
